프로그래머스 파괴되지 않은 건물 [2022 KAKAO BLIND RECRUITMENT]
https://programmers.co.kr/learn/courses/30/lessons/92344
시도1 (시간 초과)
단순한 구현 문제로 접근해보자
skill array를 하나하나 읽으면서 board에 직접 연산해보자.
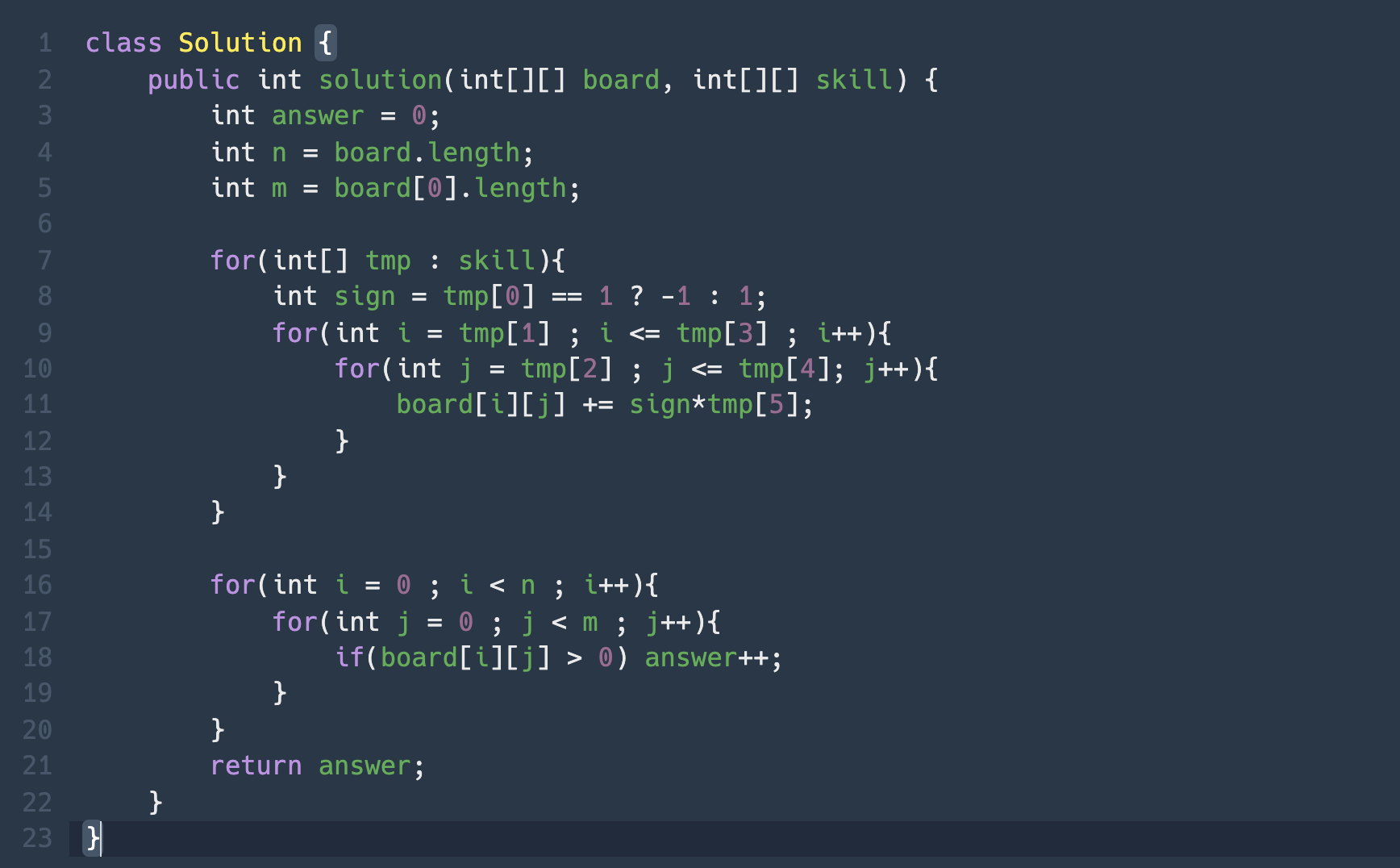
심플하게 구현할 수 있으나, 효율성 테스트에서 시간 초과에 걸리고 말았다.
K가 skill 개수, N가 board 행의 개수, M가 board 열의 개수일 때,
시간복잡도가 O(K×N×M)에 달하는데
최악의 경우 1000×1000×250,000 = 250,000,000,000번 이상의 연산을 수행해야 한다.
시도2 (성공)
누적합 알고리즘을 적용해보자
skill별로 (r1, c1)부터 (r2, c2)까지 동일하게 +sign×degree를 수행해야 한다.
board의 각 성분에 값을 직접 더하고 빼는 대신, 특정값을 어디부터 더해야 하고 어디부터 더하지 않아야 하는 지 표기해 연산을 줄일 수 있도록 '누적합 알고리즘'을 적용해보자.
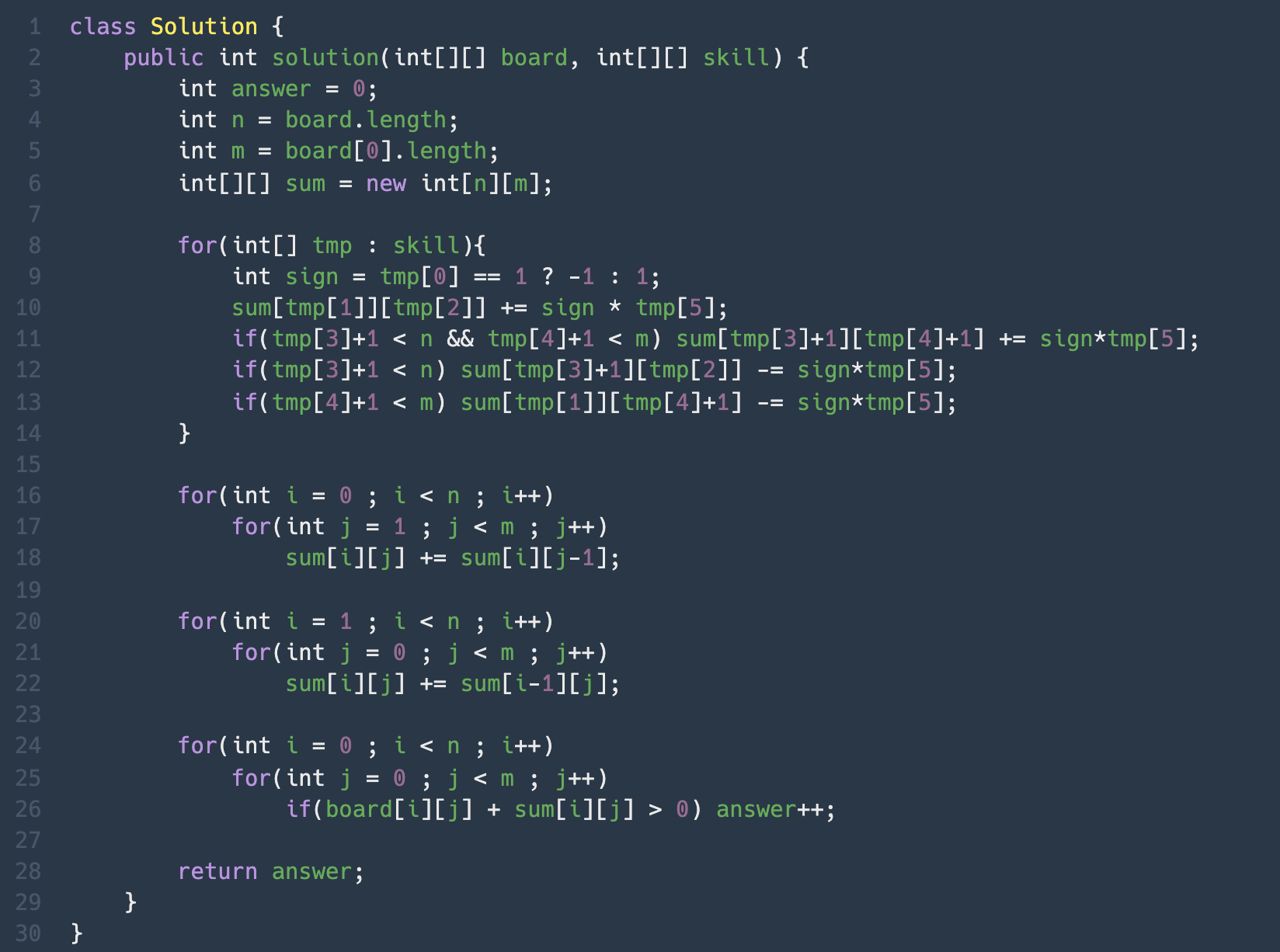
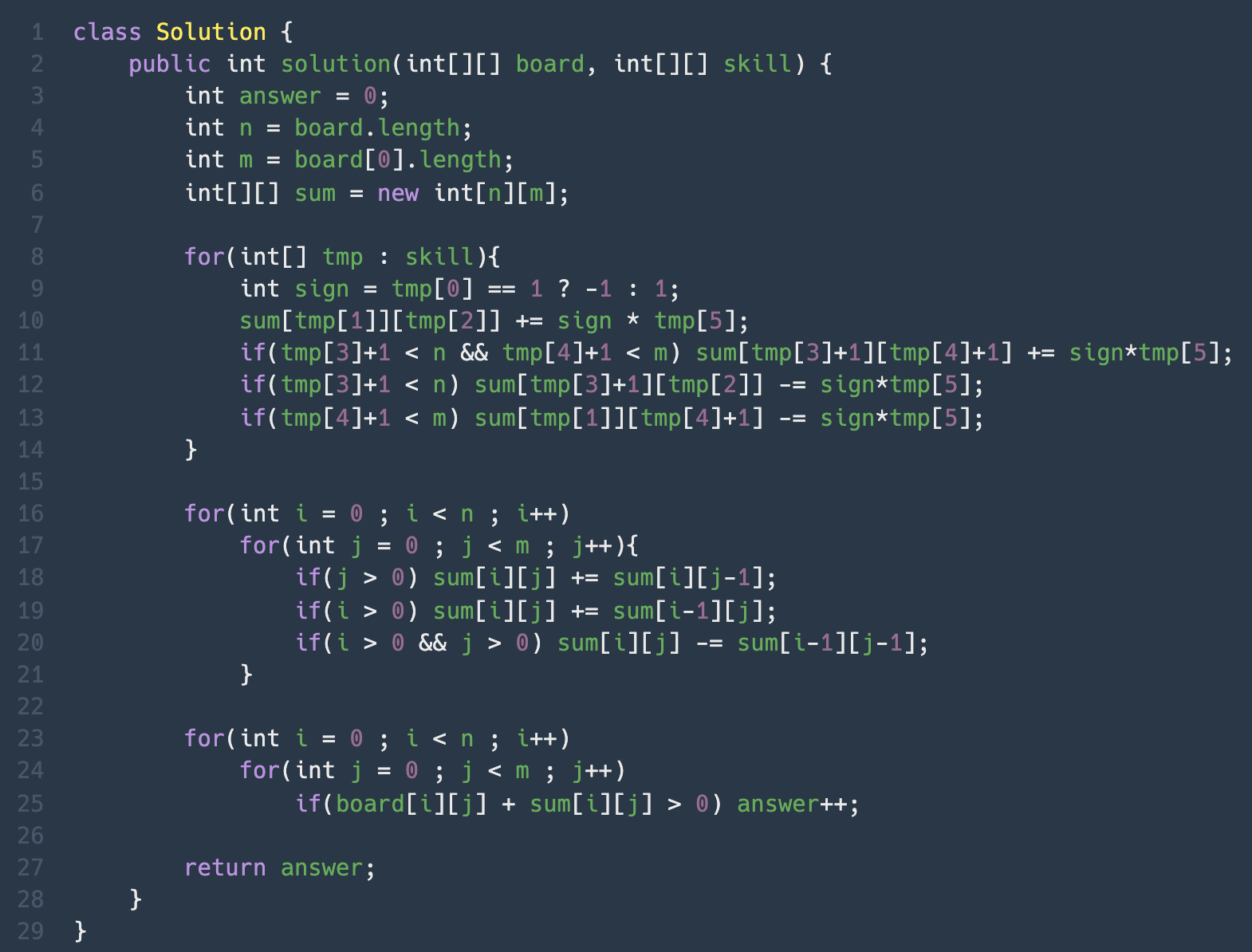
9열부터 13열까지의 코드가 담고있는 내용은 다음과 같다. (type에 따른 +, - 여부는 sign으로 대체)
- sum[r1][c1] += sign×degree // board[r1][c2]부터 sign×degree를 더한다
- sum[r2+1][c1] -= sign×degree // board[r2+1][c1]부터 sign×degree를 더하지 않는다
- sun[r1][c2+1] -= sign×degree // board[r1][c2+1]부터 sign×degree를 더하지 않는다
- sum[r2+1][c2+1] += sign×degree // 2, 3번으로 인해 중복으로 빠진 값을 상쇄
이는 16~18열의 좌-우 합산, 20~22열의 상-하 합산을 거쳐
sum[i][j]가 board[i][j]에 더해야 할 값을 의미하게 된다.
다음 그림을 보자. (sign×degree는 심플하게 a로 대체하겠다)
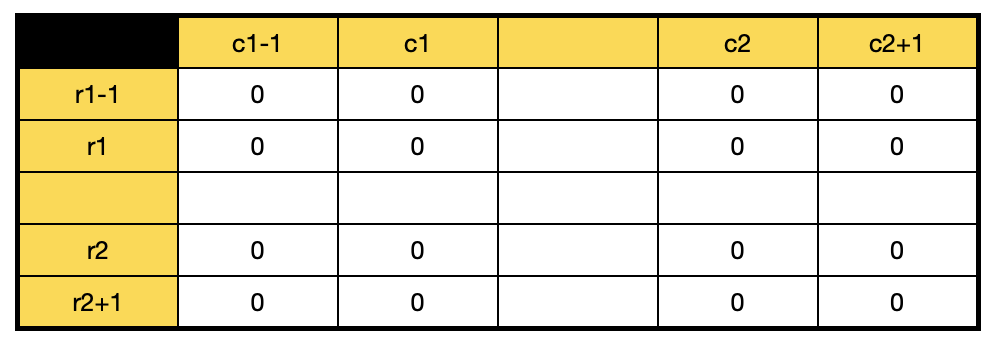
초기 연산
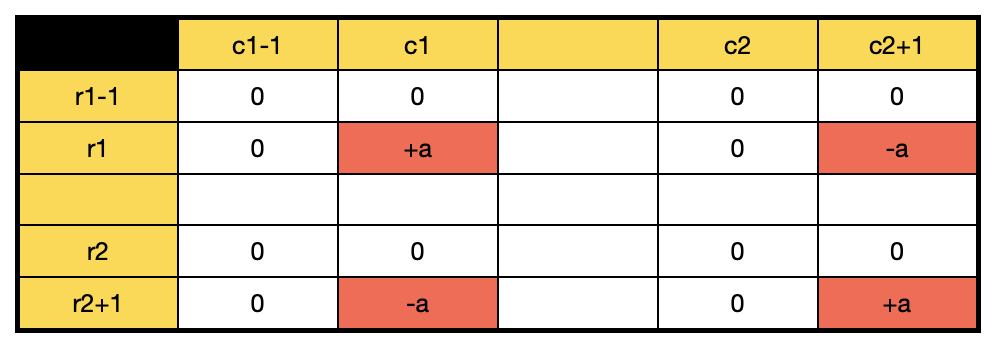
좌우 합산
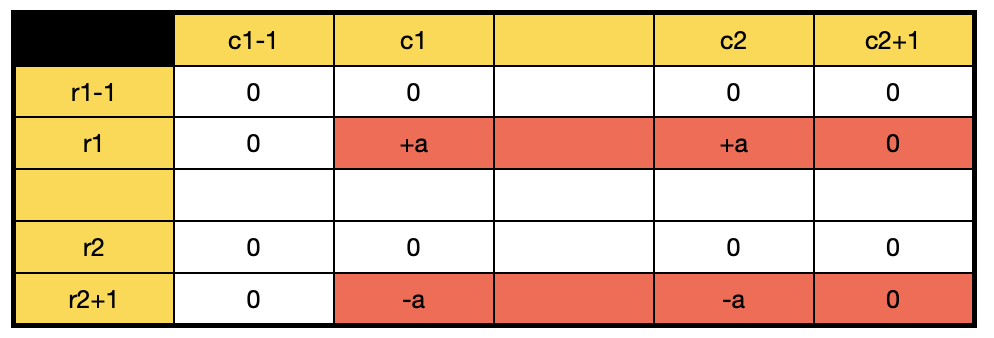
상하 합산
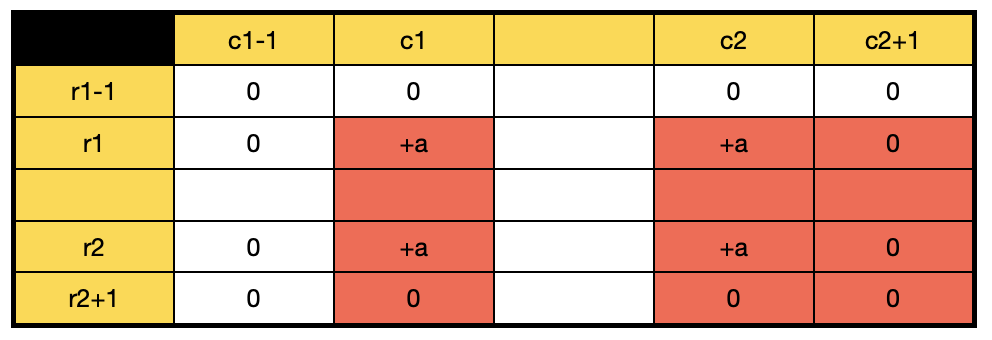
결과적으로 (r1, c1)부터 (r2, c2)까지만 +a가 적용된다.
이 경우 시간복잡도는 O(K+N×M)=O(N×M)이다.
최악의 케이스에도 250,000 + 3×1000×1000 = 3,250,000번의 연산을 수행한다.
.
.
여담1
나의 경우 좌우합산, 상하합산을 위한 for loop를 별도로 사용하였는데,
아래와 같이 한꺼번에 처리하는 것도 가능하다. 16~22열의 코드를 다음으로 수정해보자.

이 경우 수식을 조금 더 직관적으로 이해할 수 있는데,
sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1]로,
직전 열까지의 합과 직전 행까지의 합을 더한 뒤 중복된 값을 빼주면 된다.
.
.
여담2
개인적으로 edge 케이스 처리를 위해 array size를 조금 더 크게 잡고, index를 뒤틀리게 쓰는 것을 선호하지 않는다. 가독성면에서 아쉬운 코드가 된다고 생각하기 때문이다.
하지만 이런 경우 edge 케이스인지 확인하기 위해 조건문을 다는 수고로움이 있다.
(사실 나보다는 CPU가 수고해야 한다)
선호도차이라고 생각하긴 했지만, 대부분은 array size를 크게 잡고 쓰는 것을 선호하시는 것 같아 의문이 들었다.
그래서 여담1에서 수정한 코드를 기반으로 array를 크게잡고 조건문을 없앴을 때와 그렇지 않을 때의 성능을 간단하게 비교해보았다. (딱 한 차례 실행한 것이라 결과를 맹신할 수는 없겠지만)
-
여담1의 코드를 수행했을 때
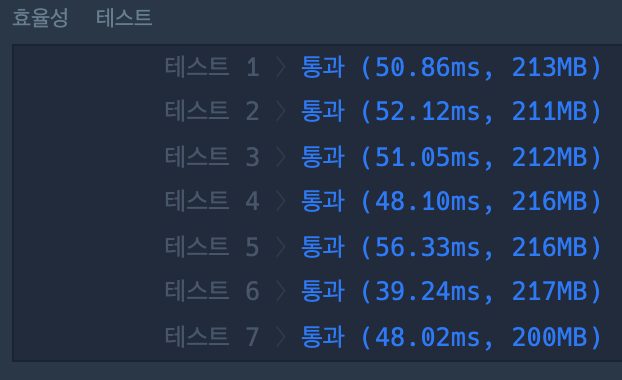
-
array를 크게 잡고 조건문을 없앴을 때
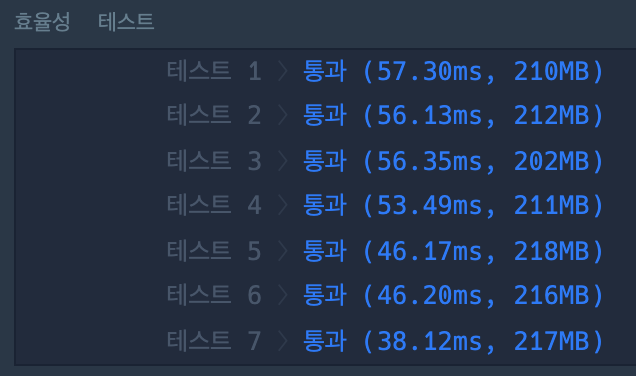
테스트케이스를 열어볼 수 없어 아쉽지만, 유의미한 차이를 발견하지 못했다.
해오던대로 계속 개발해도 괜찮겠다.
