[프로그래머스/Java] 92345번 사라지는 발판

프로그래머스 사라지는 발판 [2022 KAKAO BLIND RECRUITMENT]
https://programmers.co.kr/learn/courses/30/lessons/92345

최대 사이즈가 크지 않고, 자리를 떠날 때 마다 발판이 사라지므로 완전탐색으로 풀어도 수행시간에 문제가 없다.
따라서 DFS 바탕의 완전탐색을 이용하였고, 대부분 같은 알고리즘을 채택하신 듯 하다.

다만 문제를 풀 때 다음 지문에 주의해 보자.

다음과 같은 2가지 상황에서 패자와 승자가 정해지며, 게임이 종료됩니다.

• 움직일 차례인데 캐릭터의 상하좌우 주변 4칸이 모두 발판이 없거나 보드 밖이라서 이동할 수 없는 경우, 해당 차례 플레이어는 패배합니다.
• 두 캐릭터가 같은 발판 위에 있을 때, 상대 플레이어의 캐릭터가 다른 발판으로 이동하여 자신의 캐릭터가 서있던 발판이 사라지게 되면 패배합니다.

친절하게도 두 상황 모두 누군가가 패배하는 상황을 기준으로 기술되었다. 승패 여부는 결국 패배하는 사람이 생기며 정해지는 것이다.

게임은 항상 플레이어 A가 먼저 시작합니다. 양 플레이어는 최적의 플레이를 합니다. 즉, 이길 수 있는 플레이어는 최대한 빨리 승리하도록 플레이하고, 질 수밖에 없는 플레이어는 최대한 오래 버티도록 플레이합니다. '이길 수 있는 플레이어'는 실수만 하지 않는다면 항상 이기는 플레이어를 의미하며, '질 수밖에 없는 플레이어'는 최선을 다해도 상대가 실수하지 않으면 항상 질 수밖에 없는 플레이어를 의미합니다. 최대한 오래 버틴다는 것은 양 플레이어가 캐릭터를 움직이는 횟수를 최대화한다는 것을 의미합니다.

다음의 간단한 케이스를 보자. 딱 두 가지 플레이가 가능하다.

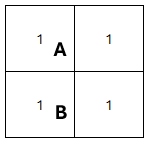
Play 1 : B가 더이상 갈 곳이 없어 패배한다.

Play 2 : A의 발판이 0이 되어 패배한다.

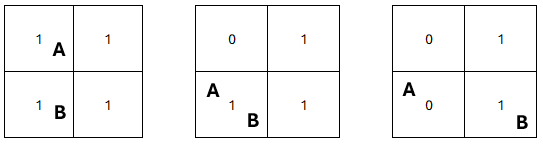
게임을 시작하는 플레이어는 A이다.
A가 무조건 이기는 건 아니지만, 첫 시도에서 오른쪽으로 이동했을 때 이길 수 있다.
따라서 A는 오른쪽으로 이동해 결국 이길 것이다.

이길 수 있는 플레이어에게 '실수만 하지 않는다면'이라는 조건이 붙은 이유가 이것이다.

DFS에서 return 값을 설정할 때 다음을 주의해보자.

각 위치에서 완전탐색으로 갈 수 있는 모든 방향을 탐색했을 때,
이길 수 있는 케이스가 있다면 그 중에서도 최선으로 이기는 케이스를 리턴한다.
질 수 밖에 없다면 최대한 오래 버티는 케이스를 리턴한다.

따라서 승패 여부와, 최적의 플레이를 할 때의 총 이동횟수를 리턴할 것이다.

class Solution {
    public static int[][] dir = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
    int boardRowLen, boardColLen;
    
    class Result{
        boolean win;
        int count;
        
        public Result(boolean win, int count){
            this.win = win;
            this.count = count;
        }
    }
    
    public int solution(int[][] board, int[] aloc, int[] bloc) {
        boardRowLen = board.length;
        boardColLen = board[0].length;
        return dfs(aloc[0], aloc[1], bloc[0], bloc[1], 0, 0, board).count;
    }
    
    public Result dfs(int ax, int ay, int bx, int by, int aDepth, int bDepth, int[][] board){
        
        boolean win = false;
        int minCount = 5*5;
        int maxCount = aDepth + bDepth;
        
        if(aDepth == bDepth && board[ax][ay] == 1){
            for(int[] tmp : dir){
                int axTmp = ax + tmp[0];
                int ayTmp = ay + tmp[1];
                if(isValid(axTmp, ayTmp, board)){
                    board[ax][ay] = 0;

                    Result d = dfs(axTmp, ayTmp, bx, by, aDepth+1, bDepth, board);
                    win |= !d.win;
                    if(!d.win) minCount = Math.min(minCount, d.count);
                    else maxCount = Math.max(maxCount, d.count);

                    board[ax][ay] = 1;
                }
            }
        } else if (aDepth > bDepth && board[bx][by] == 1){
            for(int[] tmp : dir){
                int bxTmp = bx + tmp[0];
                int byTmp = by + tmp[1];
                if(isValid(bxTmp, byTmp, board)){
                    board[bx][by] = 0;

                    Result d = dfs(ax, ay, bxTmp, byTmp, aDepth, bDepth+1, board);
                    win |= !d.win;
                    if(!d.win) minCount = Math.min(minCount, d.count);
                    else maxCount = Math.max(maxCount, d.count);

                    board[bx][by] = 1;
                }
            }
        }
        
        return new Result(win, win ? minCount : maxCount);
    }
    
    public boolean isValid(int x, int y, int[][] board){
        if(x < 0 || x >= boardRowLen || y < 0 || y >= boardColLen || board[x][y] == 0) return false;
        return true;
    }
}

aDepth는 A가 지금까지 이동한 횟수, bDepth는 B가 지금까지 이동한 횟수이다.
A가 먼저 플레이하므로, aDepth == bDepth라면 A가 플레이할 차례이고,
aDepth > bDepth라면 B가 플레이할 차례이다.

이번 턴에서 플레이 할 사람을 앞으로 X라고 지칭하겠다.

X의 자리에 발판이 없거나, 사방을 탐색했을 때 갈 수 있는 경로가 없다면 X는 그 자리에서 패배한 것이다.
따라서 패배와 함께 aDepth + bDepth를 리턴할 것이다.

반대로, X의 자리에 발판이 있고 갈 수 있는 경로가 있다면 dfs를 수행한다.
가능한 케이스 중 이길 수 있는 방법이 있다면 이기는 방법을 리턴할 것이다.

dfs를 수행할 때 마다 return받은 결과를 가지고 win |= !d.win를 수행하는데,
d에서 받은 결과는 X가 아닌 다른 사람이 리턴한 결과이므로 승패가 반대이다.
그래서 not(!)을 수행하는 것이며, dfs 중 이기는 케이스가 하나라도 있다면 win을 true로 만들기 위해 or(|) 연산을 수행한다.

이기는 케이스라면 최대한 빨리 이길 때의 총 이동횟수인 minCount를 갱신하고 지는 케이스라면 최대한 오래 버틸 때의 총 이동횟수인 maxCount를 갱신한다.

.
.

나름 불필요한 변수와 로직을 제거하였지만, 비슷한 로직이 if문과 else if문에서 되풀이되어 아쉬운 코드이다.
다른 코드를 보니, A와 B를 위한 변수를 대신 '이번 턴인 사람'과 '아닌 사람'을 나눠 작성하신 분도 있더라.

불필요한 작성을 줄일 수 있는 방식이라 내 코드에도 적용해보았다.
dfs 매개변수 중 (x1, y1)은 이번 턴인 사람의 좌표, (x2, y2)는 이번 턴이 아닌 사람의 좌표이다.

class Solution {
    public static int[][] dir = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
    int boardRowLen, boardColLen;
    
    class Result{
        boolean win;
        int count;
        
        public Result(boolean win, int count){
            this.win = win;
            this.count = count;
        }
    }
    
    public int solution(int[][] board, int[] aloc, int[] bloc) {
        boardRowLen = board.length;
        boardColLen = board[0].length;
        return dfs(aloc[0], aloc[1], bloc[0], bloc[1], 0, board).count;
    }
    
    public Result dfs(int x1, int y1, int x2, int y2, int depth, int[][] board){
        
        boolean win = false;
        int minCount = 5*5;
        int maxCount = depth;
        
        if(board[x1][y1] == 1){
            for(int[] tmp : dir){
                int x1Tmp = x1 + tmp[0];
                int y1Tmp = y1 + tmp[1];
                if(isValid(x1Tmp, y1Tmp, board)){
                    board[x1][y1] = 0;

                    Result d = dfs(x2, y2, x1Tmp, y1Tmp, depth+1, board);
                    win |= !d.win;
                    if(!d.win) minCount = Math.min(minCount, d.count);
                    else maxCount = Math.max(maxCount, d.count);

                    board[x1][y1] = 1;
                }
            }
        }
        
        return new Result(win, win ? minCount : maxCount);
    }
    
    public boolean isValid(int x, int y, int[][] board){
        if(x < 0 || x >= boardRowLen || y < 0 || y >= boardColLen || board[x][y] == 0) return false;
        return true;
    }
}

.
.

두 플레이어가 각자의 최적해를 찾아야 하기 때문에, 완전탐색, DFS 문제 중에서도 유독 독특하게 다가온 문제였다.
게임이론의 '미니맥스 알고리즘'을 알았더라면 더 쉽게 접근할 수 있었을 거라는 언급이 있었다.
기회가 된다면 다른 포스트에서 소개할 수 있기를..