본 포스팅은 David Silver 교수님의 강화학습 강의와 그 강의를 정리한 팡요랩 강의를 바탕으로 정리한 것입니다.

환경을 알지 못하는 상황에서 던져진 Agent를 이용하여 어떻게 최적의 policy를 찾을 것인가? <Control 문제>

1. Model-free control

---

1.1 model-free control의 문제점

⚠️ model-free환경에서 control문제를 해결할때는 MDP를 모르기 때문에 발생하는 여러 문제점이 존재한다.
(=$\mathcal P^a_{ss'}, \mathcal R^a_s$를 알지못한다)

• policy iteration의 원리

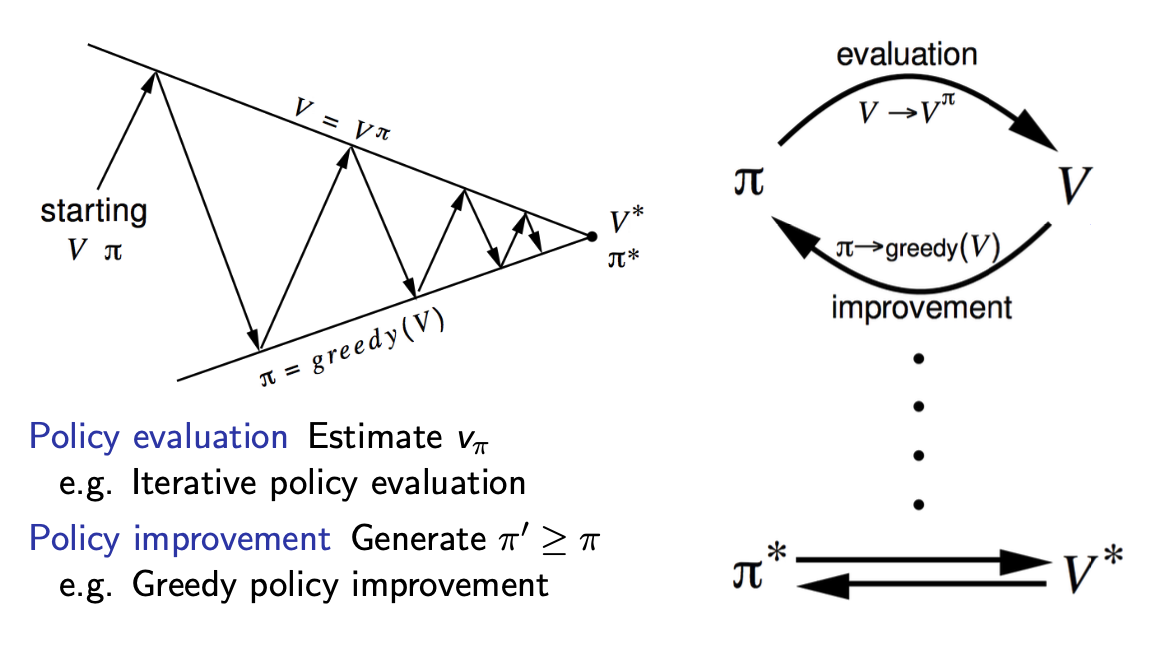
  • 기본적으로 control문제를 풀기 위해서는 policy evaluation과 policy improvement를 반복해서 수행하면서 점차 개선된 policty를 찾아나가는 과정을 필요로한다.

  • 이때, policy evaluation과 improvement 각 단계에서는 어떤 method를 적용하여도 된다.

    e.g. (model-based에서는) iterative, greedy

    

• MDP를 모를 때 발생하는 문제점

  1. Iterative policy evaluation을 적용할 수 없다.

     Iterative policy evaluation은 Bellman Expectation Equation을 기반으로 value를 계산해나가는 과정이다.

     그런데 Bellman Expectation Equation에는 MDP를 알아야만 알 수 있는 요소$^*$들이 존재하기 때문에 MDP를 알 수 없는 model-free환경에서는 이 식을 그대로 적용할 수 없다.

     • state $s$에서 action $a$를 했을 때 받는 reward는 실제로 Agent가 경험해봐야만 알 수 있다.
     • state $s$에서 action $a$을 했을 때 어떤 state $s'$에 도달하게 되는지는 실제로 Agent가 경험해봐야만 알 수 있으며, 경험을 하더라도 구체적인 확률 분포를 정의하지는 못한다.
     $v_\pi(s) =\sum_{a\in\mathcal A} \pi(a|s) \left( \mathcal R^a_s + \gamma \sum_{s'\in\mathcal S}\mathcal P^a_{ss'}v_\pi(s')\right)$

  2. $V$를 기반으로는 Greedy policy를 만들 수 없다.

     greedy policy는 state-value function을 기반으로 가장 value가 높은 next-state에 도달하게 하는 action을 선택하는 방법으로 만들어진다.

     그런데 model-free환경에서는 어떤 action $a$을 수행했을 때 어떤 state $s'$에 도달하게 되는지는 실제로 Agent가 경험해봐야만 알 수 있으며, 경험을 하더라도 구체적인 확률 분포를 정의하지는 못한다.

     따라서 어떤 action을 했을 때 최종적으로 더 높은 value를 갖는 state에 도달할 확률이 더 높은 action을 선택하는 greedy policy를 정의할 수 없다.

  *Example of Greedy Action Selection
  • problem : 2개의 문이 존재하고 각각의 문을 선택할 때마다 reward를 받게 되며, 문을 선택한 뒤에는 그 방으로 들어간다. (model-free)
    • action : 왼쪽 문을 연다, 오른쪽 문을 연다
    • state : left, right
  • episode

    1. 왼쪽 문을 열고 reward 0을 받은 뒤 왼쪽 방에 들어갔다. → $V(\text{left}) = 0$

    2. 오른쪽 문을 열고 reward 1을 받은 뒤 오른쪽 방에 들어갔다. → $V(\text{right}) = 1$

    3. 더 value가 높은 state인 right에 도달하기 위해 오른쪽 문을 열고 reward 3을 받은 뒤 오른쪽 방에 들어갔다. → $V(\text{right}) = (1+3)/2 =2$

    4. 더 value가 높은 state인 right에 도달하기 위해 오른쪽 문을 열고 reward 2을 받은 뒤 오른쪽 방에 들어갔다. → $V(\text{right}) = (1+3+2)/3 =2$

       $\vdots$
       

  • $Q$. 오른쪽 문을 여는 행동을 선택하는 것이 과연 최적의 행동이라고 확신할 수 있는가?
    $A$. 왼쪽 문을 여는 행동을 딱 한번 수행하는 것으로는 완전히 파악할 수가 없다. (e.g. 왼쪽 문을 다시 열었더니 reward $+100$이 주어질수도 있음)
    

1.2 model-free에서 Policy improvement

MDP를 모를 때 발생하는 문제점의 해결방안

• policy evaluation 단계
  즉 prediction 문제는 model-free prediction문제를 해결하는 방법론인 MC, TD를 적용하여 평가할 수 있다.
  
• policy improvement 단계
  • 더 나은 action을 평가하는 기준으로 state-value $v(s)$ 대신에 action-value $q(s,a)$를 이용한다.
  • exploration을 고려하기 위하여 $\epsilon$-greedy 방법을 이용한다.

• Greedy policy improvement

  • MDP를 알아야, $V(s)$에 대하여 greedy policy improvement를 할 수 있다.

    $=$model-free일 때는 할 수 없다!

    $\pi'(s) = \argmax_{a\in \mathcal A}\left( \mathcal R^a_s + \gamma \sum_{s'\in \mathcal S}\mathcal P^a_{ss'}V(s')\right)$

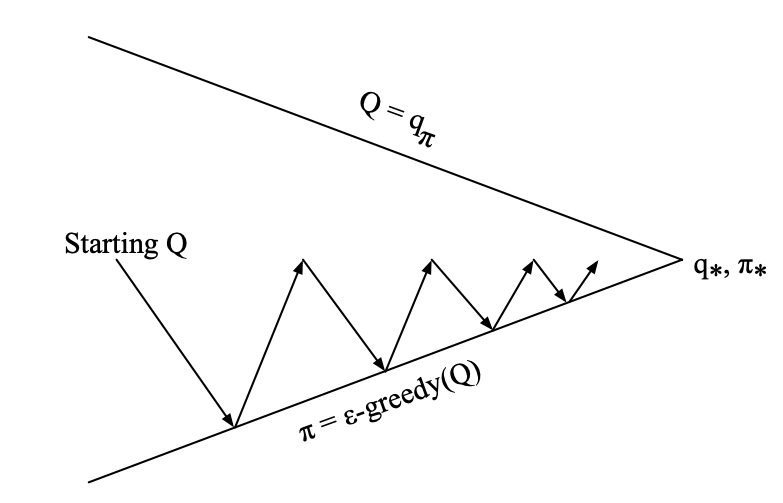
  • model-free일 때는 $Q(s,a)$에 대하여 greedy하게 action을 선택하는 방법으로서 greedy policy improvement를 수행할 수 있다.

    $\pi'(s) = \argmax_{a\in \mathcal A} Q(s,a)$
• $\epsilon$-greedy Exploration

  • Exploration이 고려되어야하는 이유

    model-based와 달리 model-free환경에서는 실제로 Agent가 action을 선택하고 state사이를 이동하면서 환경에 대한 정보를 배우게 된다. 그런데 학습의 초기 단계에서부터 greedy action만을 선택한다면 Agent가 다양한 state를 방문하지 못하고 이미 방문한 state만 계속 방문하게 될 수 있다.
    

  • 각 action이 non-zero probability를 가질 때, ($n(\mathcal A) = m$)

    • $1-\epsilon$의 probability만큼 greedy action을 선택한다. → policy가 계속 emprovement함을 보장한다.

    • $\epsilon$의 probability만큼 random action을 선택한다. → agent가 모든 state를 방문할 수 있음을 보장한다.

      $\pi(a|s) = \begin{cases} \epsilon /m +1 - \epsilon & \text{if }a^* = \argmax_{a\in \mathcal A} Q(s,a)\\ \epsilon /m & \text{otherwise}\end{cases}$

  • (Theorem) $\epsilon$-greedy policy improvement

    For any $\epsilon$-greedy policy $\pi$, the $\epsilon$-greedy policy $\pi'$ with respect to $q_\pi$ is an improvement

    $v_{\pi'} (s) \ge v_\pi(s)$

    1. state $s$에서의 action은 $\pi'$을 따라 선택하고 이후에는 $\pi$를 따라 시행했을 때의 action-value $q_\pi(s, \pi'(s))$를 bellman equation으로 표현한 것

    2. $\pi'(a|s)$를 epsilon-greedy형태로 표현한 것

       가능한 모든 action에 대하여 greedy action에 대해서는 $\epsilon/m+(1-\epsilon)$을 곱해주고 그렇지 않은 경우 그냥 $\epsilon/m$만을 곱해주었다. *(probability $\times$ value)
       

    3. geedy action에 대한 value는 다른 어떤 action-value보다도 큰 값이기 때문에 다른 action들에 대한 weighted-sum보다도 큰 값을 가진다.

       *weight는 4번째 식으로 정리하기 위해 곱해준 임의의 값

    4. 해당 수식은 $v_\pi(s)$로 표현된다. (action-value간의 관계)

       → 1-step에 대해서 더 좋음을 보이면 결국 policy improvement theorem에 의해 $v_{\pi'}(s) \ge v_\pi(s)$임을 보일 수 있다.

       $q_\pi(s, \pi'(s)) = \sum_{a\in \mathcal A}\pi'(a|s) q_\pi(s,a)$
       $=\frac{\epsilon}{m}\sum_{a\in \mathcal A}q_\pi(s,a) + (1-\epsilon)\max_{a\in \mathcal A}q_\pi(s,a)$
       $\ge \frac{\epsilon}{m}\sum_{a\in \mathcal A}q_\pi(s,a) + (1-\epsilon)\sum_{a\in \mathcal A}\frac{\pi(a|s) - \epsilon/m}{1-\epsilon}q_\pi(s,a)$
       $=\sum_{a\in \mathcal A}\pi(a|s) q_\pi(s,a) = v_\pi(s)$

1.3 on-policy와 off-policy

• On-policy Learning
  • Learn on the job
  • 학습시키려는 policy와 실제 environment에서 Agent가 경험을 쌓을 때 따르는 policy가 동일한 경우
• Off-policy Learning
  • Look over someone’s shoulder
  • 학습시키려는 policy와 실제 environment에서 Agent가 경험을 쌓을 때 따르는 policy가 다른경우

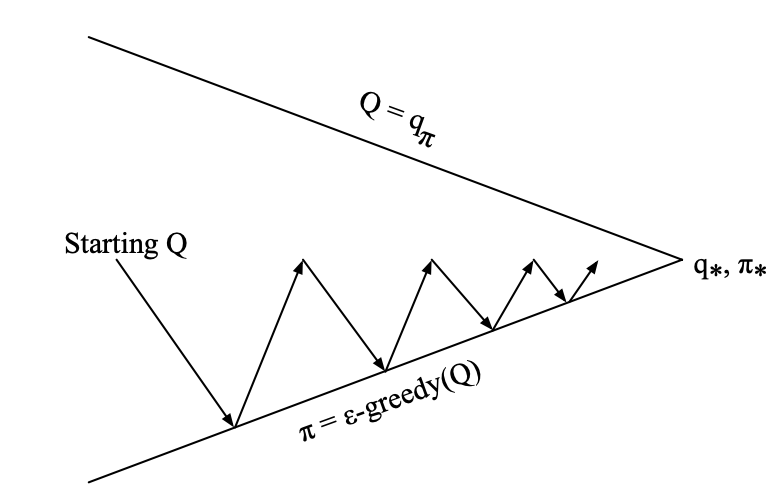
2. On-Policy Monte-Carlo Control

---

2.1 Monte-Carlo Control

for Every episode :

• Policy evaluation : Monte-Carlo policy evaluation, $Q \approx q_\pi$
• Policy improvement : $\epsilon$-greedy policy improvement

*효율적인 갱신방법 : policy evaluation을 수행할 때, $q_\pi$에 수렴할 때까지 진행하지 않고 early-stop한다.

→ Agnet가 경험한 하나의 episode에 대한 정보를 가지고 바로 더 나은 pocliy로 갱신

2.2 GLIE property

• Definition of Greedy in the Limit with Infinite Exploration : GLIE

  Greedy in the Limit with Infinite Exploration under the following conditions :

  • All state-action pairs are explored infinitely many times,

    $\lim_{k \rightarrow \infin} N_k(s,a) = \infin$
    
    

  • The policy converges on a greedy policy,

    $\epsilon$-greedy를 이용한다면 optimal Q-value를 가지고 있더라도 $\epsilon$이라는 확률만큼은 최적이 아닌 랜덤한 action을 수행하기 때문에, 결국 최적의 policy를 찾기 위해서는 최종적으로 greedy policy에 수렴해야한다.

    $\lim_{k \rightarrow \infin} \pi_k(a|s) = \bold 1(a=\argmax_{a' \in \mathcal A} Q_k(s,a'))$

  ⇒ GLIE와 $\epsilon$-greedy : 예를 들어, $\epsilon$이 점차 $0$으로 수렴한다면($=\epsilon_k = 1/k$) GLIE의 조건을 만족시킬 수 있다.
  

• GLIE Monte-Carol Control $\pi$를 따라 수행한 $k$번째 episode에서, $\{S_1, A_1, R_2, \cdots, S_T\} \sim \pi$
  • For each state $S_t$ and action $A_t$ in the episode, (in Evaluation)
    *$N(S_t, A_t)$ : 수행 횟수
    $N(S_t, A_t) \leftarrow N(S_t, A_t) + 1$
    $Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \frac{1}{N(S_t, A_t)} (G_t - Q(S_t, A_t)$
  • Improve policy based on new action-value function (in Emplovement)
    $\epsilon \leftarrow \frac{1}{k}$
    $\pi \leftarrow \epsilon\text{-greedy}(Q)$
• (Theorem) GLIE Monte-Carol Control의 수렴성

  GLIE Monte-Carlo control converges to the optimal action-value function,

  $Q(s,a) → q_*(s,a)$

2.3 MC vs. TD Control

• TD의 장점

  • MC에 비하여 Lower variance
  • Online Update
  • Incomplete sequence에도 적용가능하다.

• TD를 MC대신에 control loop에 적용하자!

  • apply TD to $Q(S,A)$
  • $\epsilon$-greedy policy improvement
  • Update every time-step

3. On-Policy Temporal-Difference Learning

---

3.1 SARSA

• SARSA: state $S$에서 action $A$를 수행하여 reward $R$을 받고 next state $S'$에 도달한 뒤, 다시 action $A'$를 수행하는 과정

• SARSA를 이용한 Action-Value function Update

  • TD Target : $R + \gamma Q(S', A')$
  • TD error : $\delta = R+\gamma Q(S', A') - Q(S,A)$
  
  
  $Q(S,A) \leftarrow Q(S,A) + \alpha (R+\gamma Q(S', A') - Q(S,A))$

• for Every time-step :

  • Policy evaluation : SARSA, $Q \approx q_\pi$

  • Policy improvement : $\epsilon$-greedy policy improvement

    

3.2 SARSA Algorithm

• SARSA 알고리즘 설명

  1. 초기에는 랜덤한 값들로 Q-table을 초기화한다.

  2. $Q$에 대한 $\epsilon$-greedy방법을 이용하여 state $S$에서의 action $A$를 고른다.

  3. action $A$를 Agent가 시행하고, 그 결과로 받게되는 reward $R$과 도달한 next-state $S'$에 대한 정보를 받는다.

  4. $Q$에 대한 $\epsilon$-greedy방법을 이용하여 이동한 state $S'$에서의 action $A'$를 선택한다.

  5. next state-action pair에 대한 Q-value를 이용하여 current Q-value를 TD방법으로 업데이트한다.

     $Q(S,A) \leftarrow Q(S,A) + \alpha (R+\gamma Q(S', A') - Q(S,A))$

  6. current state, action에 $S'$, $A'$를 대입한다.

     $\vdots$

3.3 Convergence of SARSA

• (Theorem) SARSA의 수렴성

  SARSA converges to the optimal action-value function $Q(s,a) → q_*(s,a)$, under the following conditions :

  • GLIE sequence of policies $\pi_t(a|s)$
  • Robbins-Monro sequence of step-sizes $\alpha_t$ : step size는 충분히 커야하지만, 수렴할 정도로 작아야한다.
    $\sum^\infin_{t=1} \alpha_t = \infin,\ \ \ \sum^\infin_{t=1} \alpha_t^2 < \infin$

3.4 n-step SARSA(𝝺)

• n-step SARSA($\lambda$)

  • $n=1,2,\cdots, \infin$일 때의 Q-return

    $n$만큼의 실제 reward와, $t+n$번째 step에서의 추정 value function의 합으로 표현한다.

    • $n=1$ : $q_t^{(1)} = R_{t+1} + \gamma Q(S_{t+1})$ [SARSA]
    • $n=2$ : $q_t^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma ^2Q(S_{t+2})$
      $\vdots$
      
    • $n=\infin$ : $q_t^{(\infin)} = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{T-1}R_T$ [MC]

  • n-step Q-return의 define

    $q_t^{(n)} = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1}R_{t+n} + \gamma^n Q(S_{t+n})$

  • n-step SARSA learning

    • n-step TD target : $q^{(n)}_t$

    • n-step TD error : $\delta_t = q^{(n)}_t - Q(S_t, A_t)$ ; target과 이전 예측 값의 차이

      $Q(S_t, A_t) \leftarrow Q(S_t, A_t)+\alpha(q_t^{(n)} - Q(S_t, A_t))$

• Forward View SARSA($\lambda$)

  • $q^\lambda$-return : SARSA부터 MC까지 진행했을 때의 모든 return의 평균

    • 각 n-step return $q_t^{(n)}$에 대하여 $(1-\lambda)\lambda^{(n-1)}$ weight를 적용하여 계산한다.

    • $n$이 커질수록 $\lambda$가 계속해서 곱해지게 되므로 더 작은 가중치를 가지게 된다.

      $q_t^\lambda = (1-\lambda)\sum^\infin_{n=1}\lambda^{n-1} q_t^{(n)}$
  • Forward-view SARSA($\lambda$) Update
    $Q(S_t, A_t) \leftarrow Q(S_t, A_t)+\alpha(q_t^{\lambda} - Q(S_t, A_t))$

• Backward View SARSA($\lambda$)

  • 아이디어

    • TD($\lambda$)에서 사용한 것처럼 SARSA도 eligibility traces를 적용할 수 있다.
    • 단, SARSA는 Q-function에 대해 TD를 적용하므로 각각의 state-action pair에 대해 대응되는 하나의 eligibility trace를 가진다.

  • eligibility trace

    • init : $E_0(s, a) = 0$
    • time-step $t$에서 어떤 state $s$에서 어떤 action $a$를 수행하면, $1$을 더해주고 방문하지 않았을 때는 $t-1$에서의 값에다가 $\gamma\in (0,1)$를 곱해줘서 값을 감소시킨다.
      $E_t(s,a) = \gamma\lambda E_{t-1}(s,a)+\bold 1(S_t=s, A_t = a)$

  • Backward-view SARSA($\lambda$) Update

    $\delta_t = R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t)$
    $Q(s, a) \leftarrow Q(s)+\alpha \delta_tE_t(s, a)$

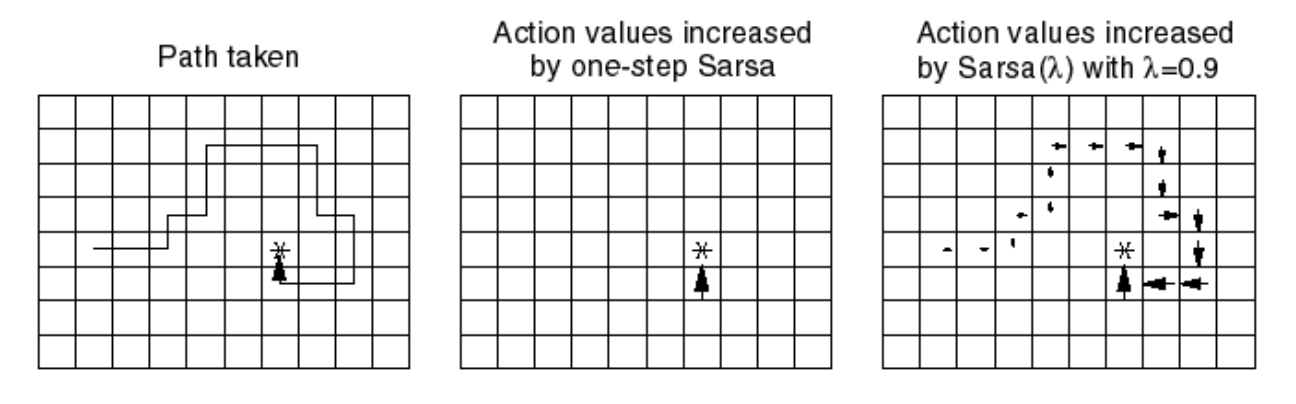
• SARSA($\lambda$)의 효율성 (Gridworld Example)
  • one-step SARSA에서는 reward를 받는 순간, 그 state에만 갱신이 된다.
  • 그러나 SARSA($\lambda$) *$\lambda \approx 1$는 reward를 받는 순간, 그 state까지 오기까지 거쳤던 모든 state, action에 대해 약간이나마 그 reward가 전파된다!

3.5 SARSA(𝝺) Algorithm

• SARSA($\lambda$) 알고리즘 설명

  1. 초기에는 랜덤한 값들로 Q-table을 초기화한다.

  2. $Q$에 대한 $\epsilon$-greedy방법을 이용하여 state $S$에서의 action $A$를 고른다.

  3. action $A$를 Agent가 시행하고, 그 결과로 받게되는 reward $R$과 도달한 next-state $S'$에 대한 정보를 받는다.

  4. $Q$에 대한 $\epsilon$-greedy방법을 이용하여 이동한 state $S'$에서의 action $A'$를 선택한다.

  5. next state-action pair에 대한 Q-value를 이용하여 current Q-value와의 차이; TD error를 계산한다.

     $\delta \leftarrow R+\gamma Q(S', A') - Q(S,A)$

  6. current state-action pair에 대한 eligibility; 방문횟수를 1 더해준다.

     $E(S,A) = E(S,A)+ 1$

  7. 모든 $s, a$에 대하여 eligibility를 고려한 만큼의 TD-error값을 더하여 Q-value를 갱신하고, 다른 실제로 방문되지 않은 state-action pair에 대해 eligibility를 감소시키는 과정을 반복한다.

     (=Q-table 전체를 업데이트 한다.)

     $Q(s,a) \leftarrow Q(s,a) + \alpha \delta E(s,a)$
     $E(s,a) \leftarrow \gamma \lambda E(s,a)$

  8. current state, action에 $S'$, $A'$를 대입한다.

     $\vdots$

4. Off-Policy Learning

---

4.1 off-policy learning

• off-policy란?

  target policy $\pi$를 따랐을 때의 value를 계산하거나, policy를 개선하고 싶을 때 target과 다른 behavior policy $\mu$를 따랐을 때의 경험적 정보를 활용하는 방법

  • target policy $\pi(a|s)$ : compute $v_\pi(s)$ or $q_\pi(s,a)$

  • behavior policy $\mu(a|s)$ : $\{S_1, A_1, R_2, \cdots, S_T\} \sim \mu$

    → 실제로 action을 sampling 할 때 사용하는 policy
    

• off-policy의 장점
  • 사람이나 다른 agent가 수행한 결과를 보고 나의 target policy를 emprovement 할 수 있다.
  • emprovement policy에 대해 다시 iterative를 수행할 때, 이미 과거에 했던 경험을 재사용할 수 있다. (=behavior policy는 update되지 않았으므로)
    
  • behavior policy가 exploration하는 경험을 바탕으로 optimal policy를 학습할 수 있다. *trade-off에서 탈출!
    
  • 하나의 behavior policy의 경험을 바탕으로 여러개의 policy들을 학습시킬 수 있다.

4.2 Importance Sampling for off-policy

• Importance Sampling

  • notation

    • $X$ : 확률분포 $P$를 따라 sampling되는 확률변수
    • $Q$ : $P$와는 다른 어떤 확률분포
    • $f(\cdot)$ : input에 대한 어떤 function

  • proof
    1. $P$를 따라 samping된 $X$에 대한 $f(X)$의 Expectation은 expectation의 definition에 의해 probability $\times$ value의 합으로 표현될 수 있다.
    2. 위 수식을 $Q$에 대한 probability로 나타내기 위하여 $Q(X)$를 분자 분모에 동일하게 곱해준다.
    3. 위 수식은 이제 $(\text{probability} = Q(X)) \times (\text{value} = (P(X)/Q(X)) \cdot f(X))$의 형태로 해석할 수 있고, 이는 $Q$를 따라 samping된 $X$에 대한 $(P(X)/Q(X)) \cdot f(X)$의 expectation으로 나타낼 수 있다!

    💡 두 확률분포의 비율만 곱해주면 어떤 확률 분포를 기반으로 구한 값에 대한 기댓값을 다른 확률 분포를 기반으로 구했을 때에 대한 기댓값으로 표현할 수 있다!

    $\mathbb E_{X \sim P}[f(X)] = \sum P(X)f(X)$
    $=\sum Q(X) \frac{P(X)}{Q(X)}f(X)$
    $=\mathbb E_{X\sim Q}\left[\frac{P(X)}{Q(X)}f(X)\right]$

• Importance Sampling for Off-policy MC

  • $G_t$를 얻을 때까지 수행한 각각이 action이 선택될 확률의 비을 계속 곱해준다.

  • return

    $G_t^{\pi/\mu}= \frac{\pi(A_t|S_t)}{\mu(A_t|S_t)} \frac{\pi(A_{t+1}|S_{t+1})}{\mu(A_{t+1}|S_{t+1})} \cdots \frac{\pi(A_T|S_T)}{\mu(A_T|S_T)} G_t$

  • Update

    $V(S_t) \leftarrow V(S_t) + \alpha\left(G_t^{\pi/\mu} - V(S_t)\right)$

  • 그러나 MC는 전체 episode가 끝난 다음에 $G_t$를 받아 계산하기 때문에, 끝날때까지 수행한 action의 수가 커지면 커질수록 $G_t$의 앞에 곱해지는 ratio가 너무 많아지기 때문에 실제로 이 방법을 사용해서 계산할 수는 없다. (ratio들의 곱에 대한 variance가 너무 큼)

    → 그렇다면 1-step해서도 수행가능한 TD는?
    

• Importance Sampling for Off-policy TD

  TD의 경우에는 앞에 곱해지는 term이 훨씬 적기 때문에 Importance sampling을 이용하여 off-policy method로 학습할 수 있다.

  $V(S_t) \leftarrow V(S_t) + \alpha\left(\frac{\pi(A_t|S_t)}{\mu(A_t|S_t)}(R_{t+1} + \gamma V(S_{t+1})) - V(S_t)\right)$

4.3 Q-Learning

• Q-Learning의 특징

  • No importance sampling required !

  • Agent가 실행할 실제 next-action은 behaviour policy를 따라 선택된다.
    $A_{t+1} \sim \mu(\cdot |S_t)$
    

  • 그러나 Q-function을 update할 때는 target policy를 따라 선택된 action $A'$에 대하여 계산한다!
    $A' \sim \pi(\cdot |S_t)$

  TD는 reward + 추측값과의 차이를 이용하여 현재값을 update하는데, 추측값에서는 behavior policy를 따르지 않아도 상관없기 때문이다.

  • update (by Bellman Equation!)
    $Q(S_t, A_t)\leftarrow Q(S_t, A_t) + \alpha(R_{t+1} + \gamma Q(S_{t+1}, A') - Q(S_t, A_t))$
  
  

• off-policy control with Q-Learning

  • (both) policy improvement

    아이디어 : behavior policy와 target policy 둘다 점차 emprovement가 되지만, behavior policy는 여전히 exploration을 고려할 수 있도록 policy를 설정하고 싶다.

    • target policy : greedy
      $\pi(S_{t+1}) = \argmax_{a'}Q(S_{t+1}, a')$
    • behavior policy : $\epsilon$-greedy

  • Q-Learning target

    target policy를 이용하여 선택된 action A’를 greedy policy에 대한 수식으로 바꾸어 표현할 수 있다.

    $R_{t+1} + \gamma Q(S_{t+1}, A')$
    $=R_{t+1} + \gamma Q(S_{t+1}, \argmax_{a'}Q(S_{t+1}. a'))$
    $=R_{t+1}+\max_{a'}\gamma Q(S_{t+1}, a')$

  • Q-Learning Update

    $Q(S, A)\leftarrow Q(S, A) + \alpha\left( R + \gamma \max_{a'} Q(S', a') - Q(S, A)\right)$

• (Theorem) Q-learning Control의 수렴성

  Q-learning control converges to the optimal action-value function,

  $Q(s,a) → q_*(s,a)$

4.4 Q-Learning Algorithm

• Q-Learning 알고리즘 설명

  1. 초기에는 랜덤한 값들로 Q-table을 초기화한다.

  2. $Q$에 대한 $\epsilon$-greedy방법을 이용하여 state $S$에서의 action $A$를 고른다.

  3. action $A$를 Agent가 시행하고, 그 결과로 받게되는 reward $R$과 도달한 next-state $S'$에 대한 정보를 받는다.

  4. $Q$에 대한 greedy방법을 ***이용하여 state $S'$에서의 action $A'$를 선택한다.*

  5. Q-Learning Update를 수행한다.

     $Q(S, A)\leftarrow Q(S, A) + \alpha\left( R + \gamma \max_{a} Q(S', a) - Q(S, A)\right)$

  6. current state, action에 $S'$만 대입한다.

     $\vdots$

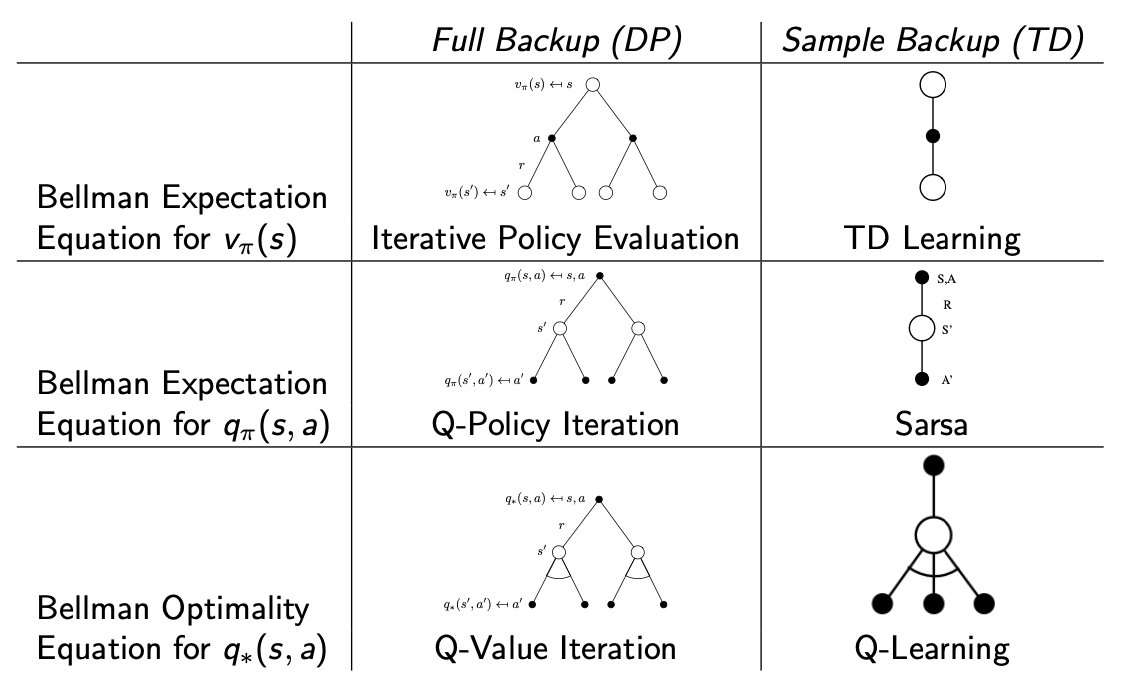
Summary

Relationship Between DP and TD

(where $x\overset{\alpha}{\leftarrow} y \equiv x \leftarrow x + \alpha(y-x)$

Reference

• Introduction to Reinforcement Learning by David Silver
• 팡요랩 : 강화학습의 기초 이론