[강화학습] Model Free Prediction

Vaughan·2023년 1월 30일

MC model free td

강화학습

목록 보기

5/6

본 포스팅은 David Silver 교수님의 강화학습 강의와 그 강의를 정리한 팡요랩 강의를 바탕으로 정리한 것입니다.

환경을 알지 못하는 상황에서 던져진 Agent를 이용하여 어떻게 value function을 추정할 것인가? <Prediction 문제>

1. Model-Free Prediction

1.1 Model-Free?

Environment의 MDP에 대한 정보를 알지 못하는 상황
MDP를 모른다?
- 내가 어떤 action을 했을 때 받는 reward $R_{t}$ 를 사전에 알지 못한다. → 직접 경험해봐야 알 수 있다.
- 내가 어떤 action을 했을 때 어떤 next-state로 transition할지를 결정하는 transition probability $\mathcal P^a_{ss'}$ 를 알지 못한다.
  - 직접 경험해봐야 어떤 next-state에 도달했는지를 알 수 있다.
  - 많이 경험하더라도 어떤 정확한 “확률 분포”를 알 수 없다.

1.2 Model-Free일 때 문제의 종류

prediction 문제 : MDP를 모를 때, value function을 구하는 과정
control 문제 : MDP를 모를 때, 최적의 optimal policy를 찾는 과정 → (next chapter)

2. Monte-Carlo Learning

2.1 Monte-Carlo Policy Evaluation

Mote-Carlo method?
- 실제로 구하기 어려운 값을 계산할 때, Agent의 “경험”을 기반으로 구해진 실제 값들을 이용하여 추정하는 방법
- (in prediction)
  
  prediction 문제에는 Agent가 따르는 “policy”가 정의되어있기 때문에 실제로 agent가 해당 policy를 따라서 environment를 경험하도록 한다. 이를 하나의 episode라고 한다.
  
  episode를 수행하면서 얻은 각각의 실제 return 값을 저장하고 평균을 구하면, value를 계산할 수 있다.
  
  → value function의 definition이 return의 expectation이기 때문!
$\text{value} = \text{mean Return}$
- 하나의 episode가 완전히 끝나야 return을 알 수 있기 때문에 모든 episode가 반드시 종료된다는 조건을 만족할 때만 적용할 수 있다는 단점을 가진다.
Policy Evaluation의 목적 : agent가 policy $\pi$ 를 따라 경험한 episode를 이용하여 $v_\pi$ 를 찾는 것
Monte-Carlo 방법의 적용
- return : total discounted reward $G_t = R_{t+1}+\gamma R_{t+2} + \cdots + \gamma^{T-1}R_T$
- value function : expected return $v_\pi(s) = \mathbb E_\pi[G_t|S_t=s]$

2.2 MC Update

가정 : Agent가 모든 state $s\in \mathcal S$ 를 방문해야한다.

why? $N(s) → \infin$ 에 근접해야하기 때문
First-visit MC Update : Agent가 해당 state에 처음 방문 했을 때만, 방문횟수를 증가시키고 return을 더한다.

To evaluate state $s$ ,
1. Increment counter
  
  $N(s) ← N(s) +1$
2. Increment total return
  
  $S(s) ← S(s) + G_t$
3. Mean return
  $V(s) = \frac{S(s)}{N(s)}$
  ⇒ 큰 수의 법칙; law of large number에 따라 $N(s) → \infin$ 에 가까워질수록 $V(s) → v_\pi(s)$ 에 수렴한다.
Every-visit MC Update: Agent가 해당 state에 방문 할 때마다, 방문횟수를 증가시키고 return을 더한다.

To evaluate state $s$ ,
- for every time-step $t$ in each episode
  1. Increment counter
    
    $N(s) ← N(s) +1$
  2. Increment total return
    
    $S(s) ← S(s) + G_t$
- Mean return $V(s) = \frac{S(s)}{N(s)}$ ⇒ 큰 수의 법칙; law of large number에 따라 $N(s) → \infin$ 에 가까워질수록 $V(s) → v_\pi(s)$ 에 수렴한다.

2.3 Incremental Mean을 이용한 MC Update

*한번에 평균을 구하여 업데이트를 하는 것이 아니라 하나의 에피소드가 끝날때마다 조금씩 평균을 업데이트 하는 방법

Incremental Mean
- 점진적으로 평균을 구하는 방법
- mean $\mu_1, \mu_2$ 는 sequence $x_1, x_2, \cdots$ 가 구해짐에 따라 다음과 같이 점진적으로 증가시키면서 update할 수 있다.
  $\mu_k = \frac{1}{k}\sum^k_{j=1}x_j$
  $=\frac{1}{k}\left(x_k + \sum^{k-1}_{j=1} x_j \right)$
  $=\frac{1}{k}(x_k+(k-1)\mu_{k-1})$
  $=\mu_{k-1}+\frac{1}{k}(x_k - \mu_{k-1})$
```
   
```
MC Update
- Incremental Mean을 이용하면 $V(s)$ 를 episode하나가 끝난 뒤에 incrementally update할 수 있다.
- for each state $S_t$ with return $G_t$ $N(S_t) \leftarrow N(S_t) +1$ $V(S_t) \leftarrow V(S_t)+\frac{1}{N(S_t)}(G_t - V(S_t))$ → 실제값 $G_t$ 와 학습중인 value $V(S_t)$ 의 차이; error만큼 조금씩 업데이트 한다.
- $N(S_t)$ 를 사용하지 않는 경우
  - $1/N(S_t)$ 가 아닌, 어떤 고정된 상수 $\alpha$ 를 곱해서 업데이트 하는 방법
  - $1/N(S_t)$ 는 자주 방문할 수록 점점 작아지기 때문에 기존 방법은 최신 episode보다 과거의 episode에 대해 더 중요하게 가정했다면, 이 방법에서는 과거의 episode를 forget하는 효과를 보일 수 있다.
  - non-stationary problem문제*에서는 이렇게 update하는 방법이 더 효과적일 수 있다.
    *non-stationary problem : MDP가 일정하지 않고 조금씩 변화하는 문제

V(S_t) \leftarrow V(S_t)+\alpha(G_t - V(S_t))

3. Temporal-Difference Learning

3.1 Temporal-Difference Policy Evaluation

Temporal-Difference method의 아이디어
- Agent의 “경험”을 기반으로 추정하는 방법
- TD는 incomplete episode에서도 업데이트 할 수 있다.
- TD updates a guess towards a guess
  
  💡 1-step을 더 진행하면 1-step만큼의 실제정보(=reward)가 반영되기 때문에 더 정확한 value를 가지고 있을 것이다 !

Policy Evaluation의 목적 : agent가 policy $\pi$ 를 따라 경험한 episode를 이용하여 $v_\pi$ 를 찾는 것
Temporal-Difference 방법의 적용
- MC policy evaluation : value를 실제 return $G_t$ 과의 차이를 이용해 update $V(S_t) \leftarrow V(S_t)+\alpha(G_t - V(S_t))$
- TD learning algotithm : value를 1-step을 더 진행했을 때, 추정된 return $R_{t+1}+\gamma V(S_{t+1})$ 과의 차이을 이용하여 update
  - TD target : $R_{t+1} + \gamma V(S_{t+1})$
  - TD error : $\delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t)$ ; target과 실제 값의 차이
    $V(S_t) \leftarrow V(S_t)+\alpha(\red{R_{t+1} + \gamma V(S_{t+1})} - V(S_t))$

3.2 n-step TD

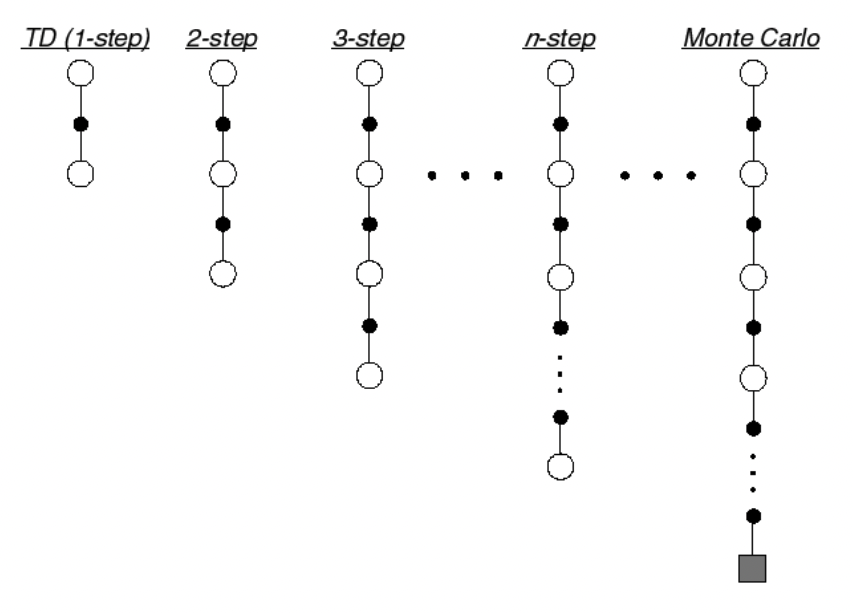
TD를 적용할 때는 1-step만 진행하고 바로 update를 진행할 수도 있지만, 여러번의 step을 진행하고 나서 그 때의 값을 이용하여 update하는 방법을 사용할 수도 있다.

→ 이때 terminal state까지의 step을 경험한뒤에 update하는 방법은 MC와 동일하다!

n-step Return
- $n=1,2,\cdots, \infin$ 일 때의 return
  
  $n$ 만큼의 실제 reward와, $t+n$ 번째 step에서의 추정 value function의 합으로 표현한다.
  - $n=1$ : $G_t^{(1)} = R_{t+1} + \gamma V(S_{t+1})$ [TD]
  - $n=2$ : $G_t^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma ^2V(S_{t+2})$
    $\vdots$
  - $n=\infin$ : $G_t^{(\infin)} = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{T-1}R_T$ [MC]
- n-step return의 define $G_t^{(n)} = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1}R_{t+n} + \gamma^n V(S_{t+n})$

n-step TD learning
- n-step TD target : $G^{(n)}_t$
- n-step TD error : $\delta_t = G^{(n)}_t - V(S_t)$ ; target과 실제 값의 차이
  $V(S_t) \leftarrow V(S_t)+\alpha(G_t^{(n)} - V(S_t))$

🍎 TD(0)과 MC사이에는 둘의 효과를 극대화할 수 있는 가장 적절한 sweet-spot이 존재한다.

3.3 Forward View of TD(𝝺)*

Averaging n-Step Returns
- 여러가지의 n-step을 따라 수행해서 구한 return이 있을 때, 각각의 return을 평균한 값을 사용하여 학습해도 된다! (combine)
- e.g. 2-step and 4-step return의 average $\frac{1}{2}G^{(2)} + \frac{1}{2}G^{(4)}$
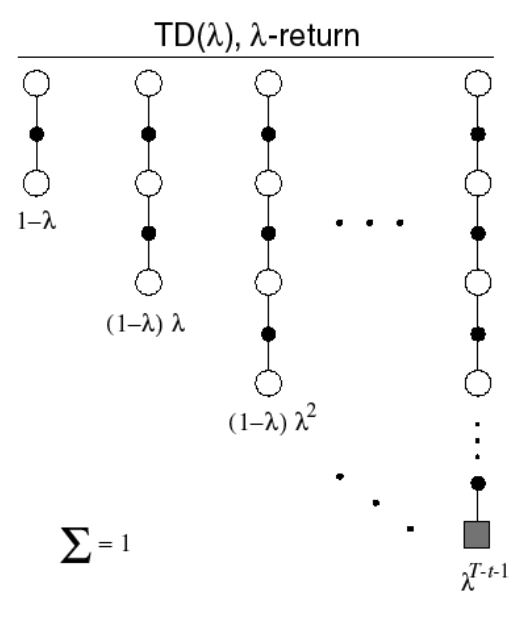
- $\lambda$ -return : TD(0)부터 MC까지 진행했을 때의 모든 return의 평균 $G^\lambda_t$
  - 각 n-step return $G_t^{(n)}$ 에 대하여 $(1-\lambda)\lambda^{(n-1)}$ weight를 적용하여 계산한다.
  - $n$ 이 커질수록 $\lambda$ 가 계속해서 곱해지게 되므로 더 작은 가중치를 가지게 된다.
    $G_t^\lambda = (1-\lambda)\sum^\infin_{n=1}\lambda^{n-1} G_t^{(n)}$
- TD( $\lambda$ ) weighting function
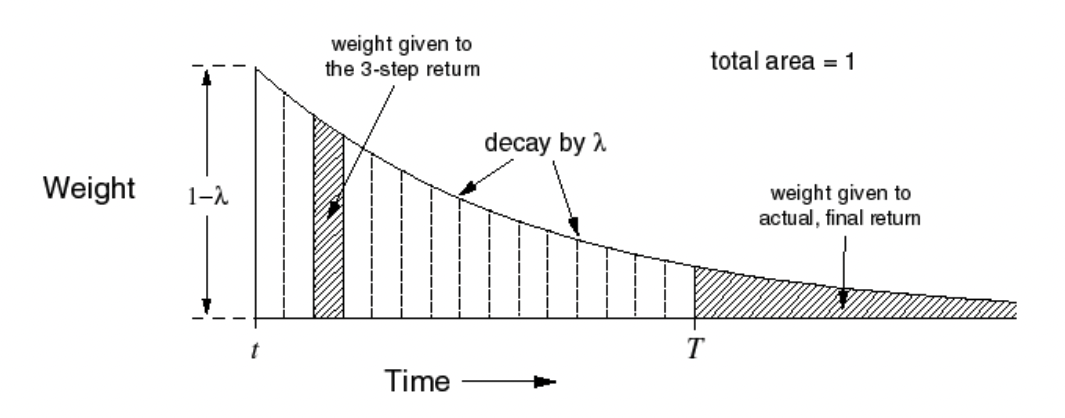
Forward-view TD( $\lambda$ )
- 작은 step만이 아닌, 미래를 보고 update한다.
- MC에서 사용하는 return도 사용하기 때문에 episode가 끝나야 계산할 수 있다.
  
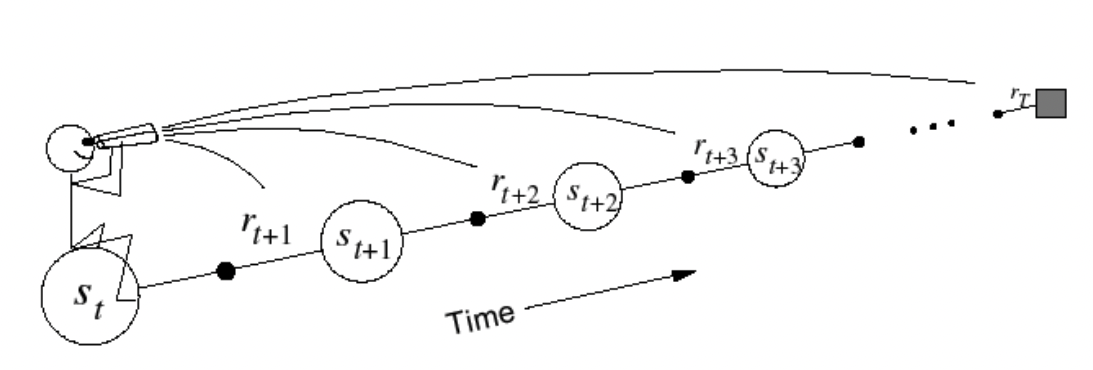
  $V(S_t) \leftarrow V(S_t)+\alpha(G_t^{\lambda} - V(S_t))$

3.4 Backward View of TD(𝝺)*

Eligibility trace $E_t(s)$

어떤 사건이 일어났을 때, 그 사건에 대한 책임이 가장 큰 요소를 더 많이 update하는 방법
- $Q$ . 누가 책임이 가장 큰지는 어떻게 판단하는가?
- 아이디어 : heuristic을 이용하자!
  - Frequency heuristic : 가장 자주 일어난 state의 책임이 크다.
  - Recency heuristic : 가장 최근에 일어난 state의 책임이 크다.
- Eligibility trace
  - init : $E_0(s) = 0$
  - time-step $t$ 에서 어떤 state s에 방문하면, $1$ 을 더해주고 방문하지 않았을 때는 $t-1$ 에서의 값에다가 $\gamma\in (0,1)$ 를 곱해줘서 값을 감소시킨다. $E_t(s) = \gamma\lambda E_{t-1}(s)+\bold 1(S_t=s)$
  - 시간에 따른 eligibility trace의 변화
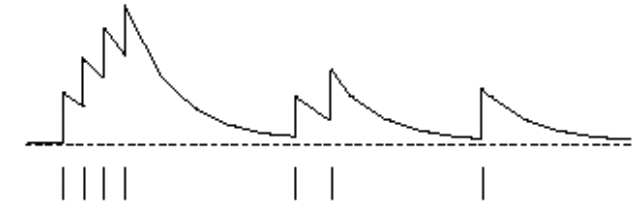
TD-error
$\delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t)$
Backward-view TD( $\lambda$ )
- TD(0)와 TD( $\lambda$ )의 장점을 모두 가진다.
  - online(매 step)마다 update할 수 있다.
  - episode가 끝나지 않는 환경에서도 사용할 수 있다.
- $t$ 일때의 TD-error에 대해 그 상황에서의 eligibility trace값을 곱한만큼 update한다. → 수학적으로 TD( $\lambda$ )와 동일함
  
  $V(s) \leftarrow V(s)+\alpha \delta_tE_t(s)$

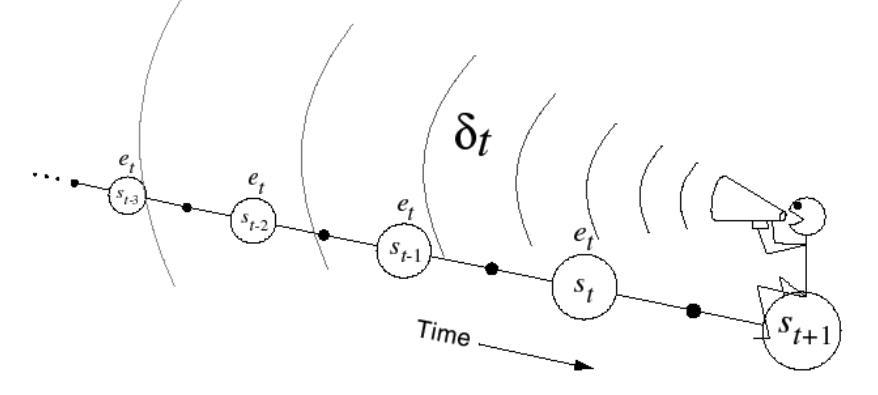
3.5 Forward and Baackward Equivalance*

TD( $\lambda$ ) and TD(0)
- $\lambda=0$ 일 때, 오직 current state만이 update된다.
  - eligibility trace
  - $E_t(s) = \bold 1(S_t=s)$
- TD(0) update
  $V(S_t) \leftarrow V(S_t)+\alpha \delta_t$
TD( $\lambda$ ) and TD(1) and MC
- $\lambda=1$ 일 때, episode의 끝까지 고려하게된다.
- Theorem
  
  The sum of offline updates is identical for forward-view and backward-view TD( $\lambda$ )
  $\sum^T_{t=1} \alpha\delta_tE_t(s) = \sum^T_{t=1} \alpha \left(G_t^\lambda - V(S_t)\right) \bold 1 (S_t=s)$
- eligibility trace
  $E_t(s) = \gamma\lambda E_{t-1}(s)+\bold 1(S_t=s)$ $=\begin{cases} 0 & \text{if }t<k \\ \gamma^{t-k} & \text{if } t\ge k \end{cases}$
- update : online
  $\sum^{T-1}_{t=1} \alpha\delta_tE_t(s) = \alpha\sum^{T-1}_{t=k}\lambda^{t-k}\delta_t =\alpha \left(G_t - V(S_k)\right)$
- total error
  $\delta_k + \gamma\delta_{k+1}+ \gamma^2\delta_{k+2} + \cdots+ \gamma^{T-1-k}\delta_{T-1}$
- MC error의 표현
  
  $\delta_k + \gamma\delta_{k+1}+ \gamma^2\delta_{k+2} + \cdots+ \gamma^{T-1-k}\delta_{T-1}$
  
  $=R_{t+1} + \gamma V(S_{t+1})-V(S_t)$
  
  $+ \gamma R_{t+2} + \gamma^2 V(S_{t+2}) - \gamma V(S_{t+1})$
  
  $+ \gamma^2 R_{t+3} + \gamma^3 V(S_{t+3}) - \gamma^2 V(S_{t+2})$
  
  $\ \ \ \vdots$
  
  $+ \gamma^{T-1-t} R_{T} + \gamma^{T-t} V(S_{T}) - \gamma^{T-1-t} V(S_{T-1})$
  
  $=R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots + \gamma^{T-1-t} R_T - V(S_t)$
  
  $=G_t - V(S_t)$

Forward and Backwards TD( $\lambda$ )
- For general $\lambda$ , TD errors also telescope to $\lambda$ -error, $G_t^\lambda - V(S_t)$
  
  $G_t^\lambda - V(S_t)$
  
  $= -V(S_t) + (1-\lambda)\lambda^0 (R_{t+1} + \gamma V(S_{t+1}))$
  
  $+ \ (1-\lambda)\lambda^1 (R_{t+1} + \gamma R_{t+2} + \gamma^2 V(S_{t+2}))$
  
  $+ \ (1-\lambda)\lambda^2 (R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \gamma^3 V(S_{t+3}))$
  
  $+\ \cdots$
  
  $= -V(S_t) + (\gamma\lambda)^0 (R_{t+1} + \gamma V(S_{t+1})-\gamma\lambda V(S_{t+1}))$
  
  $+\ (\gamma\lambda)^1 (R_{t+2} + \gamma V(S_{t+2})-\gamma\lambda V(S_{t+2}))$
  
  $+\ (\gamma\lambda)^2 (R_{t+3} + \gamma V(S_{t+3})-\gamma\lambda V(S_{t+3}))$
  
  $+\ \cdots$
  
  $= (\gamma\lambda)^0 (R_{t+1} + \gamma V(S_{t+1}) - V(S_t))$
  
  $+\ (\gamma\lambda)^1 (R_{t+2} + \gamma V(S_{t+2})-V(S_{t+1}))$
  
  $+\ (\gamma\lambda)^2 (R_{t+3} + \gamma V(S_{t+3})-V(S_{t+2}))$
  
  $+\ \cdots$
  $=\delta_t + \gamma\lambda\delta_{t+1} + (\gamma\lambda)^2\delta_{t+2} + \cdots$

TD 총정리*

4. MC vs. TD

4.1 Non Episodic MDP

TD는 final outcome이 산출되기 전에 학습할 수 있다.
- TD는 각각의 모든 step에서 online으로 학습이 가능하다.
- MC는 반드시 episode의 끝에 도달할 때까지 기다리고 return을 알게되면 그때 학습한다.
TD는 final outcome 없이도 학습할 수 있다.
- TD는 non-teriminatinh 환경에서도 적용할 수 있다.
- MC는 오직 episodic(=terminating)한 환경에서만 적용할 수 있다.

4.2 Bias / Variance trade-off

bias와 variance
- bias
  - return $G_t$ 는 $v_\pi(S_t)$ 에 대한 unbiased estimate이다.
    
    즉, value function의 정의에 따라 $G_t$ 를 계속 sampling하면 결국 $v_\pi(S_t)$ 에 수렴할 것이다.
  - true TD target $R_{t+1}+\gamma v_\pi(S_{t+1})$ 은 $v_\pi(S_t)$ 에 대한 unbiased estimate이지만, 우리는 $v_\pi$ 의 실제 값을 알지 못한 상태에서 계산하기 때문에 TD target은 $R_{t+1} + \gamma V(S_{t+1})$ 은 biased estimate이다.
    
    추정값을 이용하여 갱신하기 때문에 발생하는 biase가 존재하고 따라서 수없이 많이 반복하더라도 TD target이 실제 $v_\pi(S_t)$ 에 정확히 수렴하리라는 보장은 가질 수 없다.
- variance
  - TD target은 반드시 return보다 더 작은 variance를 가진다.
  - why?
    Return은 수많은 랜덤한 action, transition, reward를 이용하여 계산되지만 TD target은 딱 한번의 랜덤한 action, transition, reward에 의해 계산되기 때문이다.
    → 1-step에서 발생할 수 있는 랜덤성은 episode가 끝날 때까지 발생할 수 있는 랜덤성보다 훨씬 작다.
  - variance가 클수록 그 확률분포에서 어떤 것을 sampling 했을 때 뽑힌 sample들에대한 편차가 클 수 있다. → 정확성이 떨어진다.

MC는 high variance, zero bias
- (function approximation $^{[1]}$ 에서도) 수렴성이 좋다.
- initial value에 그다지 민감하지 않다.
- 이해하고 사용하기 간단하다.
TD는 low variance, some bias
- MC보다 대부분 더 효율적이다.
- TD(0)은 $v_\pi(s)$ 로 수렴하긴 하지만, function approzimation에서는 수렴함이 보장되지 않는다.
- MC에 비하여 더 initial value에 민감하다.

4.3 Batch MC and TD

MC와 TD의 수렴성
- $\infin$ 번 experience할 수 있다면 $V(s) → v_\pi(s)$ 로 반드시 수렴한다는 것은 알고 있다.
- 그런데 만약 k개의 제한된 episode만을 가지고 있을 때, MC와 TD는 수렴하는가? $s^1_1, a^1_1, r^1_2, \cdots, s^1_{T_1}$ $\vdots$ $s^k_1, a^k_1, r^k_2, \cdots, s^k_{T_k}$
AB Example
- problem
  - state : A, B
  - 아래의 8개의 episode에 대한 정보만을 알고 있을 때 $V(A), V(B)$ 의 값은?
- MC와 TD에서의 value
  - MC : $V(A)= 0$
    전체 episode에서 A에 도달한 경우는 1번인데 그때의 return이 0이므로
  - TD : $V(A) = 0.75$
    $V(A)$ 는 reward $0+V(B)$ , 즉 V(B)의 value를 이용하여 갱신되기 때문이다.

certainty Equivalence
- MC : minimum MSE
  $\sum^K_{k=1}\sum^{T_k}_{t=1} (G_t^k - V(s^k_t))^2$
- TD(0) : max likelihood Markov model
  $\hat{\mathcal P}^a_{s, s'} = \frac{1}{N(s,a)}\sum^K_{k=1} \sum^{T_k}_{t=1} \bold 1(s^k_t, a^k_t, s^k_{t+1} = s, a, s')$ $\hat{\mathcal R}^a_{s} = \frac{1}{N(s,a)}\sum^K_{k=1} \sum^{T_k}_{t=1} \bold 1(s^k_t, a^k_t = s, a)r^k_t$
  → 한정된 개수의 episode를 이용할 때는 MC와 TD를 사용하여 계산했을 때 value에 차이가 발생한다.
  
  따라서,
- TD는 Markov property를 사용하여 value를 추측한다. → Markov 환경에서 더 효율적이다.
- MC는 Markov property를 사용하지 않고 value를 추측한다. → non-Markov 환경에서 더 효율적이다.

4.4 More difference

Backup 방법의 차이
- Monte-Carlo Backup : DFS $V(S_t) \leftarrow V(S_t) + \alpha(G_t- V(S_t))$
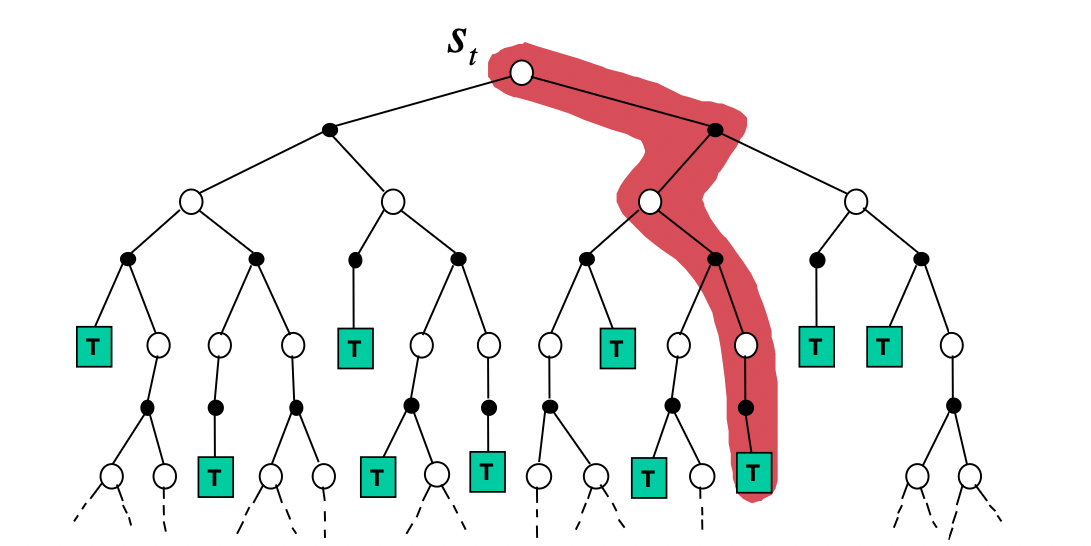
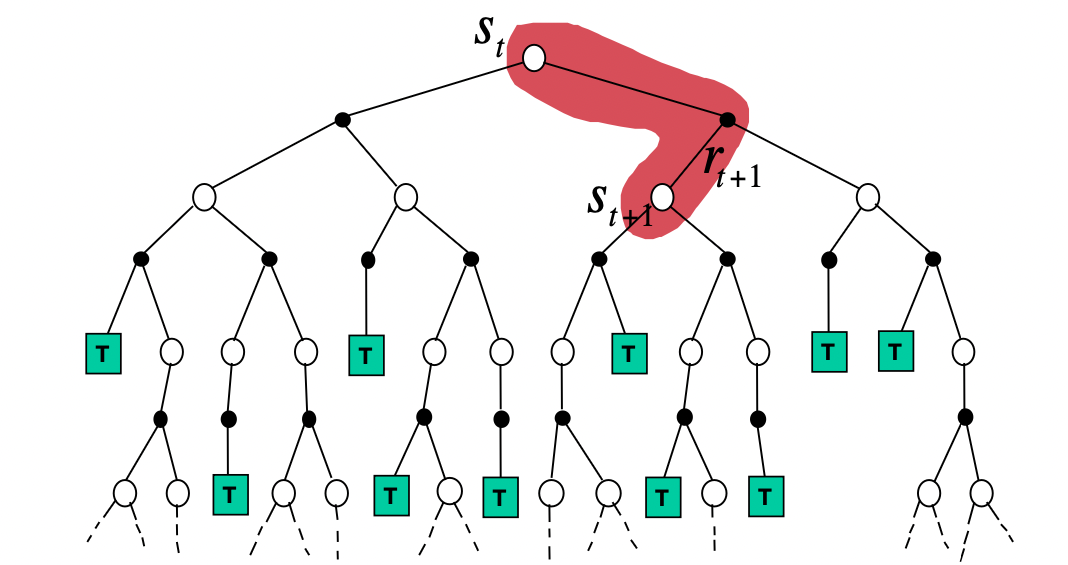
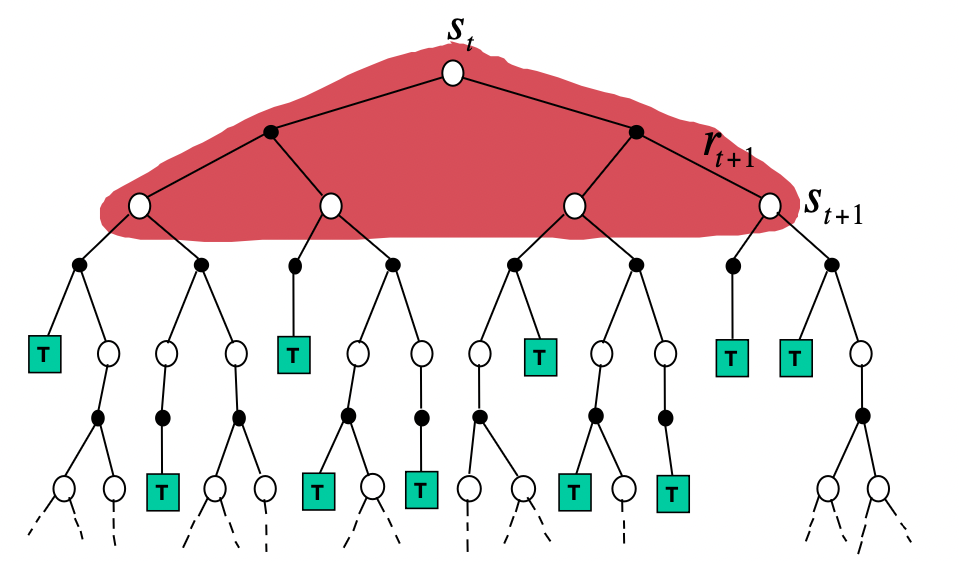
- Temporal-Difference Backup : (1-step) <Bootstraping> $V(S_t) \leftarrow V(S_t) + \alpha(R_{t+1}+\gamma V(S_{t+1})- V(S_t))$
- Dynamic Programming Backup : BFS $V(S_t) \leftarrow V(S_t) + \alpha(R_{t+1}+\gamma V(S_{t+1})- V(S_t))$
Bootstrapping & Sampling
- Bootstrapping : update involves an estimate
  - DP : bootstraps
  - MC : does not bootstraps
  - TD : bootstraps
- Sampling : update samples an expectation ****
  - DP : does not sample (sampling을 하지않고 가능한 모든 action에 대한 값을 이용한다.
  - MC : samples
  - TD : samples

(bootstrapping & sampling 관점에서) RL method의 총정리*

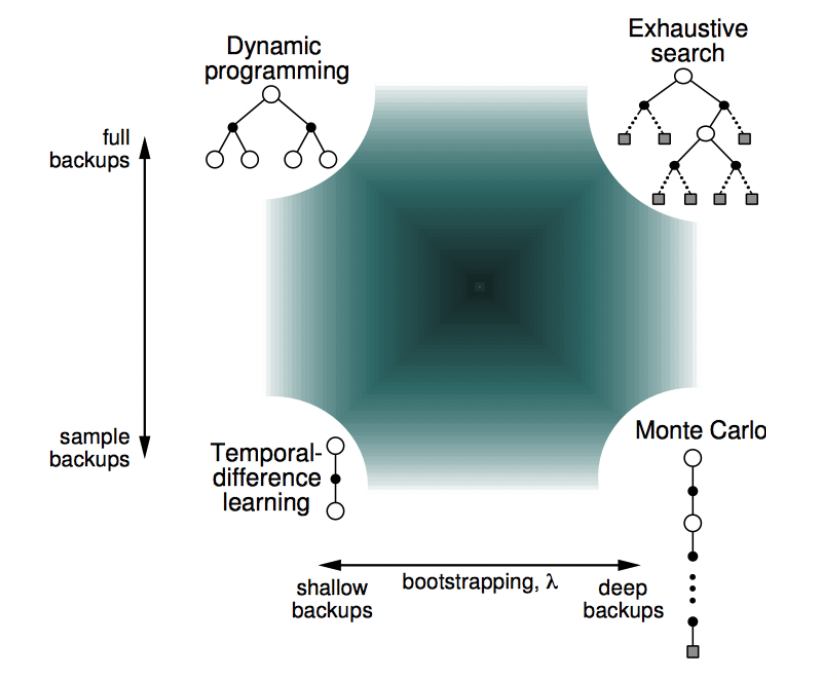
4.5 with Example

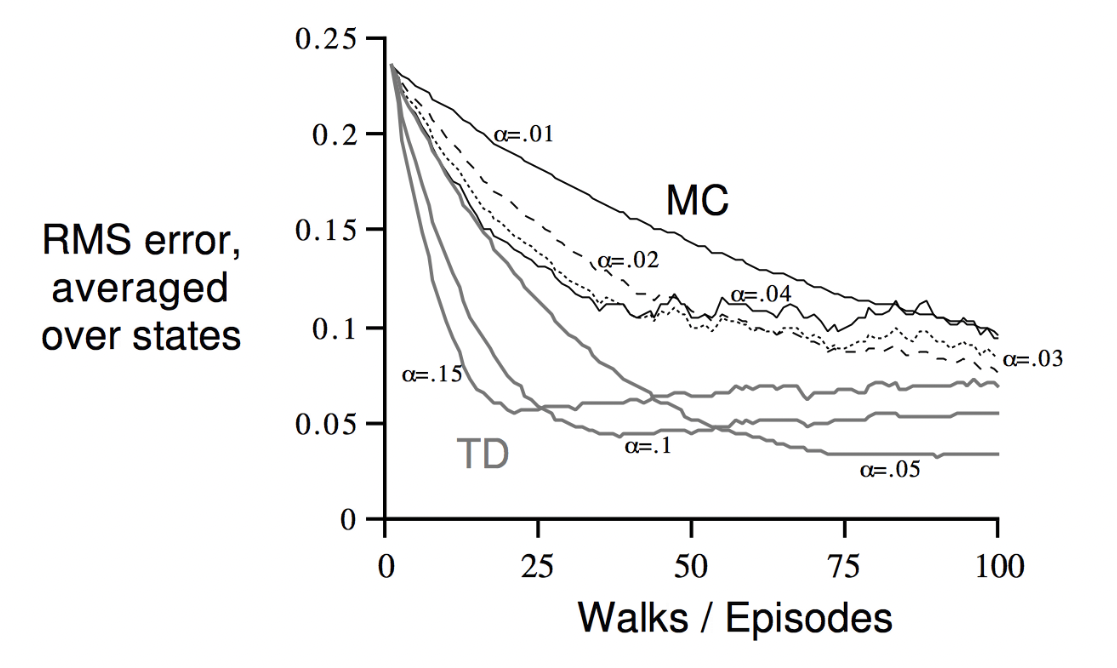
Random Walk Example

problem : policy를 평가
- state : A, B, C, D, E
- teminal state : ▪️
- policy : left / right 랜덤하게 움직인다.
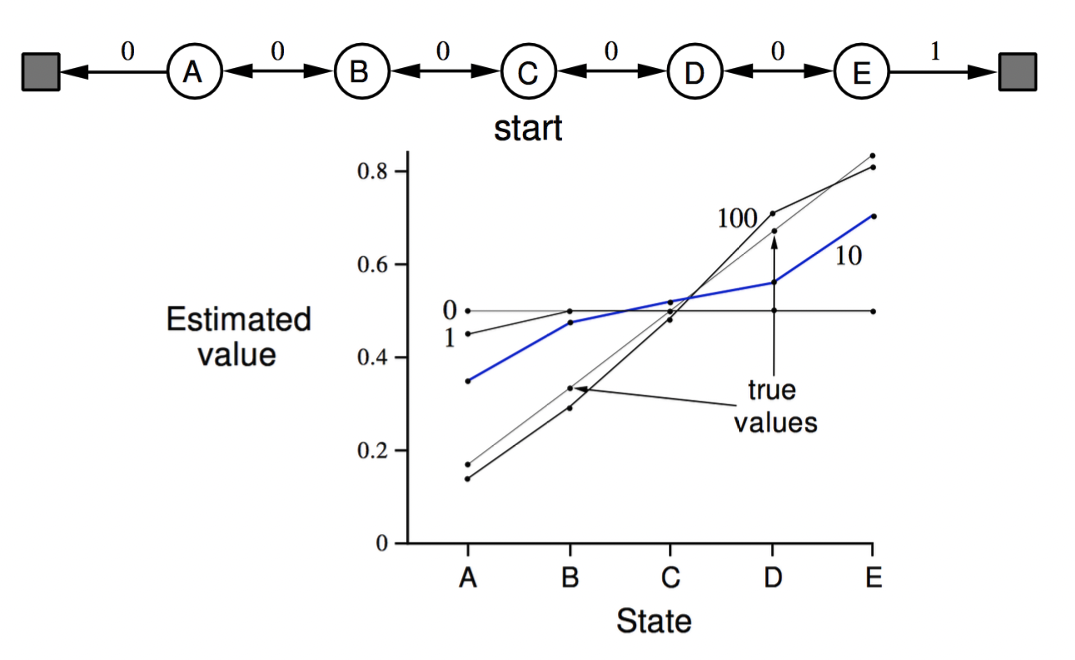
MC vs. TD (with. $\alpha$ 값에 따른 변화) → error는 실제 value function과의 RMS로 표현

Reference

Vaughan

우주의 아름다움도 다양한 지식을 접하며 스스로의 생각이 짜여나갈 때 불현듯 나를 덮쳐오리라.