확률론 맛보기

• 목차
  • 딥러닝에서 확률론이 필요한 이유
  • 이산확률변수 vs 연속확률변수
  • 확률분포는 데이터의 초상화이다.
  • 조건부확률과 기계학습
  • 기대값이란
  • 몬테카를로 샘플링

딥러닝에서 확률론이 필요한 이유

• 딥러닝은 확률론 기반의 기계학습 이론에 바탕을 두고 있음
• 기계학습에서 사용되는 손실함수(loss function)들의 작동원리는 데이터 공간을 통계적으로 해석해서 유도하게 됨
  • 예측이 틀릴 위험(risk)을 최소화하도록 데이터를 학습하는 원리는 통계적 기계학습의 기본 원리임
  • 분산 및 불확실성을 최소화하기 위해서는 측정하는 방법을 알아야 함
• 회귀: $L_2$-노름은 예측오차의 분산을 가장 최소화하는 방향으로 학습하도록 유도
• 분류: 교차엔트로피(Cross-entropy)는 모델 예측의 불확실성을 최소화하는 방향으로 학습하도록 유도

  데이터 공간을 $X$ x $Y$라 표기하고 $D$는 데이터공간에서 데이터를 추출하는 분포임

이산확률변수 vs 연속확률변수

• 확률변수는 확률분포 $D$에 따라 이산형(discrete)과 연속형(continuous) 확률변수로 구분하게 됨.(데이터 공간에 의해 결정되는 것이 아니라 $D$에 의해 결정됨)
• 이산형 확률변수는 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링 함.
  

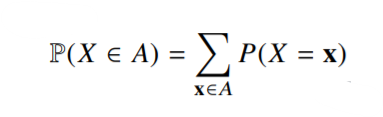
  $P(X=x)$는 확률변수가 x값을 가질 확률로 해석할 수 있음

• 연속형 확률변수는 데이터 공간에 정의된 확률변수의 밀도(density) 위에서의 적분을 통해 모델링 함.
  

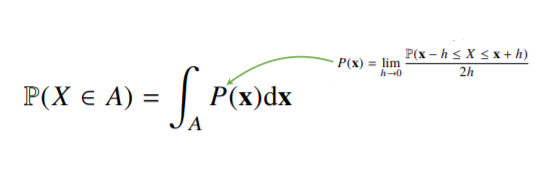
  밀도는 누적확률분포의 변화율을 모델링하며 확률로 해석하면 안 됨.

확률분포는 데이터의 초상화이다

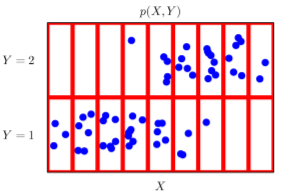
• 결합분포 $P(X, Y)$는 $D$를 모델링함.(원래분포 D와 모델링한 결합분포는 다를 수 있음(모델링 방법에 따라 결정됨. 달라도 근사할 수 있음, 이산 -> <- 연속)
• $D$는 이론적으로 존재하는 확률분포이기 때문에 사전에 알 수 없음.
• $P(X)$는 입력 X에 대한 주변확률분포로 Y에 대한 정보를 주진 않음.

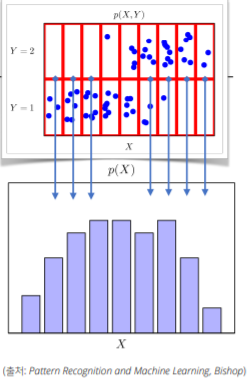
• 입력 X에 대한 주변확률분포인 $P(X)$는 결합분포 $P(X, Y)$에서 유도 가능함(모델링에 따라)
  • 주변확률분포는 결합확률분포 $P(X, Y)$를 각각의 Y에 대해서 모두 더해주거나 적분을 통해 유도할 수 있음

조건부확률과 기계학습

• 조건부확률분포 $P(X|Y)$는 데이터 공간에서 입력 X와 출력 Y사이의 관계를 모델링 함(특정 클래스가 주어진 조건에서 데이터의 확률분포를 보여줌)
  

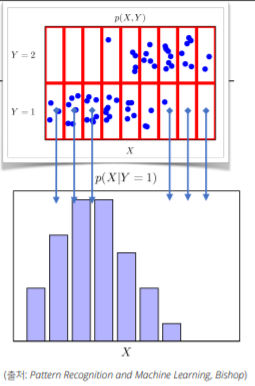
  • Y가 1인 경우의 조건부확률(특정 클래스) -> 데이터의 초상화, 데이터를 해석하는 데 필요한 도구 !!

• (주의)연속확률분포의 경우 $P(Y|X)$는 확률이 아니고 밀도임.

• 선형모델과 소프트맥스 함수의 결합(로지스틱)은 데이터에서 추출된 패턴을 기반으로 확률을 해석하는데 사용됨.

• 분류와 회귀에서의 조건부확률
  

기대값이란

• 기대값은 데이터를 대표하는 통계량이다(=평균(MEAN))
  • 연속확률분포: 함수에 확률밀도함수를 곱해서 적분한다.
  • 이산확률분포: 함수에 확률질량함수를 곱해서 급수(수열의 합)를 구한다.

• 기계학습에서는 기대값을 통해 여러 통례량(분산, 첨도, 공분산 등)을 계산할 수 있다.
  

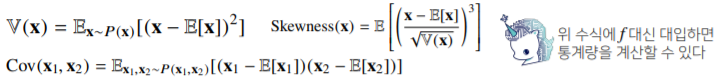
몬테카를로(Monte Carlo) 샘플링

• 확률분포를 모를 때 데이터를 이용하여 기대값을 계산하려면 몬테카를로 샘플링 방법을 사용한다.
  

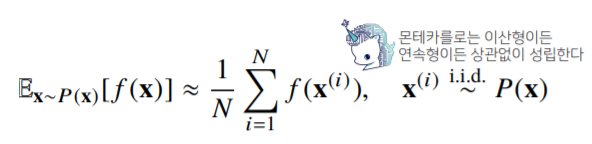
  식과 같이, 데이터를 대입한 후, 산술평균을 계산하면 기대값에 근사한다.

• 몬테카를로 샘플링은 독립추출만 보장된다면 대수의 법칙(law of large number)에 의해 수렵성을 보장한다.
  • 대수의 법칙: 큰 모집단에서 무작위로 뽑은 표본의 평균이 전체 모집단의 평균과 가까울 가능성이 높다.