
확률론 맛보기
- 목차
- 모수란?
- 확률분포 가정하기(예시)
- 데이터로 모수 추정하기
- 최대가능도 추정법
- 최대가능도 추정법 예제: 정규분포
- 최대가능도 추정법 예제: 카테고리 분포
- 딥러닝에서 최대가능도 추정법
- 확률분포의 거리
- 쿨백-라이블러 발산
모수란?
- 통계적 모델링은 적절한 가정 위에서 확률분포를 추정(근사적으로)하는 것이 목표이다.
- 통계적 모델링은 어떤 가정을 미리 부여하는가에 따라 모수적 방법론과 비모수적 방법론으로 나뉘게 된다.
- 모수적(parametric) 방법론: 데이터가 특정 확률분포를 따른다고 선험적으로(a priori) 가정한 후 그 분포를 결정하는 모수(parameter)(평균과 분산)를 추정하는 방법
- 비모수(nonparametric) 방법론: 특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌는 것(모수가 없는 것이 아니라 모수가 데이터에 따라 유연하게 바뀌거나 무한한 것임.)(기계학습의 대부분의 방법론)
확률분포 가정하기(예시)
- 확률분포를 가정하는 방법: 히스토그램(통계치 등등)을 통해 모양을 관찰한다.
- 베르누이 분포: 데이터가 2개의 값(0 or 1)만 가지는 경우
- 카테고리 분포: 데이터가 n개의 이산적인 값을 가지는 경우(베르누이의 다차원 형태)
- 베타분포: 데이터가 [0, 1] 사이에서 값을 가지는 경우
- 감마분포, 로그정규분포 등: 데이터가 0이상의 값을 가지는 경우
- 정규분포, 라플라스분포 등: 데이터가 전체에서 값을 가지는 경우
데이터로 모수 추정하기
- 데이터의 확률분포를 가정했다면, 모수를 추정해볼 수 있다.
- 정규분포의 모수는 평균 와 분산 으로 이를 추정하는 통계량은 다음과 같다.
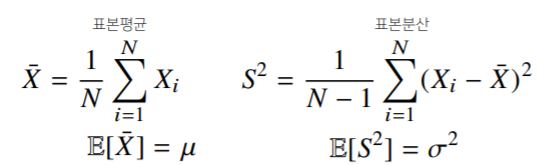
- 통계량의 확률분포를 표집분포(sampling distribution)라 부르며, 특히 표본평균의 표집분포는 N이 커질수록 정규분포을 따른다.
- 이를 중심극한정리(Central Limit Theorem)이라 부르며, 모집단의 분포가 정규분포를 따르지 않아도 성립한다.
- 표집표본 != 표본분포
최대가능도 추정법
-
표본평균, 표본분산은 확률분포마다 사용하는 모수가 다르므로 적절한 통계량이 달라지게 됨.
-
이론적으로 가장 가능성이 높은 모수를 추정하는 방법 중 하나: 최대가능도 추정법(maximum likelihood estimation, MLE)
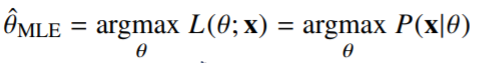
- : 데이터가 주어져있는 상황에서 를 변형시킴에 따라 값이 바뀌는 함수(주어진 데이터 x에 대하여 모수 를 변수로 둔 함수)(likelihood 함수를 최적화하는 를 찾는 것.)
- 가능도(likelihood)함수는 모수 를 따르는 분포가 x를 관찰할 가능성을 뜻하지만, 확률로 해석하면 안 된다(대소비교를 위한 함수임).
-
데이터 집한 X(행벡터)가 독립적으로 추출되었을 경우 로그가능도를 최적화한다.
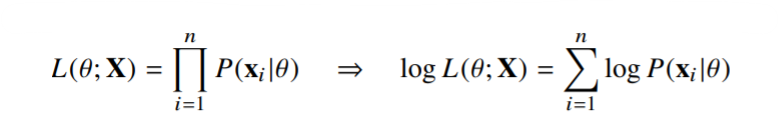
왜 로그가능도를 사용하는가?
- 데이터가 엄청나게 많아지면 컴퓨터의 정확도로는 가능도를 계산하는 것이 불가능하다. 이때, 로그를 사용하면(데이터가 독립인 경우) 가능도의 곱셈을 가능도의 덧셈으로 바꿀 수 있기 때문에 컴퓨터로 연산이 가능해진다.
- 경사하강법으로 가능도를 최적화할 때 미분 연산을 하게 되는데, 로그가능도를 사용하면 연산량을 에서 으로 줄일 수 있다.
-
대게의 손실함수의 경우 경사하강법을 사용하므로 음의로그가능도(negative log-likelihood)를 최적화하게 된다.
- 경사하강법은 '목적식을 최소화하는 것'이기 떄문에 '최대'가능도에 negative를 함
최대가능도 추정법 예제: 정규분포
- 정규분포를 따르는 확률변수 X로부터 독립적인 표본{}을 얻었을 때 최대가능도 추정법을 이용하여 모수를 추정하면?
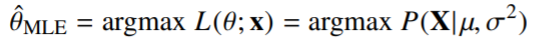
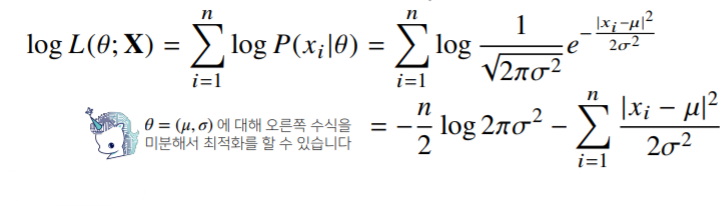
- 정규분포의 확률밀도함수
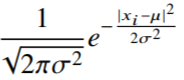
- 분산
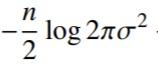
- 분산, 평균
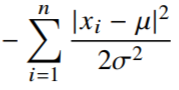
- 정규분포의 확률밀도함수
- 위 두 식(분산, 평균)을 미분하여 최적화를 할 수 있음
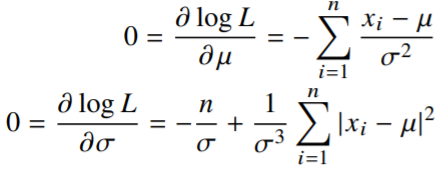
두 미분이 모두 0이 되는 를 찾으면 가능도를 최대화하게 된다.
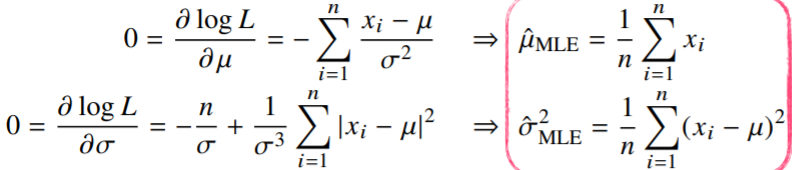
최대가능도 추정법 예제: 카테고리 분포(이산, 베르누이의 다차원 형태)
- 카테고리 분포 Multinoulli)를 따르는 확률변수 X로부터 독립적인 표본 {}을 얻었을 때 최대가능도 춪어법을 이용하여 모수를 추정하면?
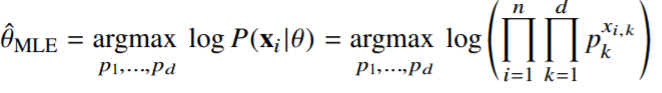
- : 주어진 데이터 의 k번째 차원에 해당하는 값
- 0이되면 1
- 1이되면
- 카테고리 분포의 모수는 다음과 같은 제약식을 만족해야 함.
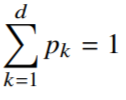
- : 주어진 데이터 의 k번째 차원에 해당하는 값

: 주어진 데이터 에 대하여 k값이 1인 데이터의 개수를 세는 것.
- 정리하면, 다음과 같이 제약식(오른쪽)을 만족하면서 왼쪽 목적식을 최대화하는 것이 우리가 구하는 MLE이다.
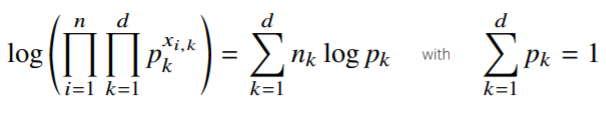
- 이때, 라그랑주 승수법을 통해 최적화 문제를 풀 수 있다(제약식과 목적식을 합침)
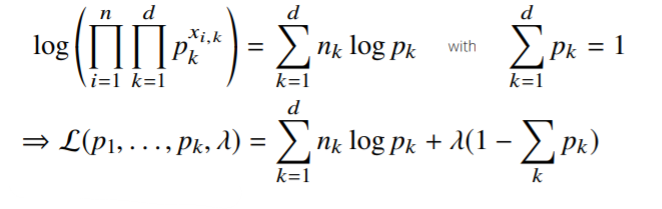
- 여기서 와 에 대하여 미분을 하면,
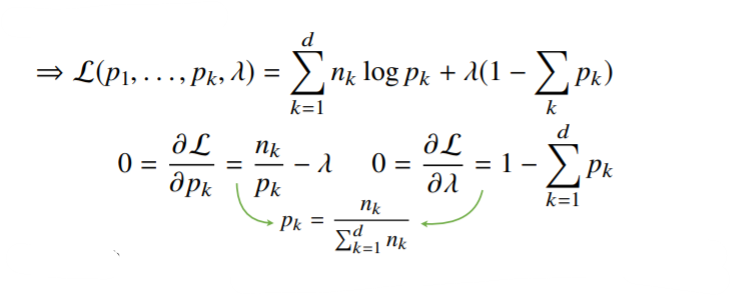
- 분모: 데이터의 개수를 다 더해준 것
- 결국 카테고리 분포의 MLE는 경우의수를 세어서 비율을 구하는 것임.
딥러닝에서 최대가능도 추정법
- 최대가능도 추정법을 이용하여 기계학습 모델을 학습할 수 있다.
- 딥러닝 모델의 가중치를 라 표기했을 때 분류문제에서 소프트맥스 벡터는 카테고리분포의 모수를 모델링한다.
- 원핫벡터로 표현한 정답레이블 을 관찰데이터로 이용해 확률분포인 소프트맥스 벡터의 로그가능도를 최적화할 수 있다.
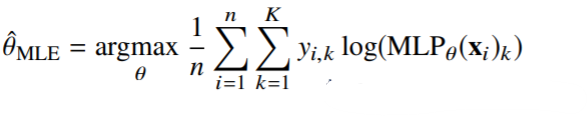
확률분포의 거리
- 기계학습에서 사용되는 손실함수들은 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도한다.
- 데이터 공간에 두 개의 확률분포 P(x), Q(x)가 있을 경우 두 확률분포사이의 거리를 계산할 때 다음과 같은 함수들을 이용한다.
- 총변동거리(Total Variation Distance, TV)
- 쿨백-라이블러 발산(Kullback-Leibler Divergence, KL)
- 바슈타인 거리(Wasserstein Distance)
쿨백-라이블러 발산
- 쿨백-라이블러 발산은 다음과 같이 정의한다.
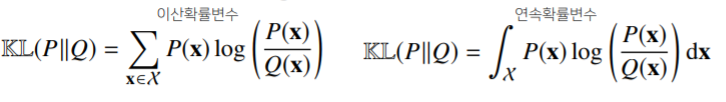
- 쿨백-라이블러 발산은 다음과 같이 분해할 수 있다.
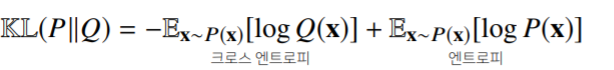
분류문제에서 정답레이블을 P, 모델 예측을 Q라 두면 최대가능도 추정법은 쿨백-라이블러 발산을 최소화하는 것과 같다.
--> 확률분포 사이에 거리를 최소화하는 것과 로그가능도 함수를 최대화시킨다는 개념은 밀접히 연결되어 있다.(ML에서 Loss 함수들과 최적화는 MLE관점에서 많이 유도가 되었다.)
추가자료: Dive into Deep Learning, Zhang et al.
(16장 추천시스템도 확인해볼 것)
