Introduction
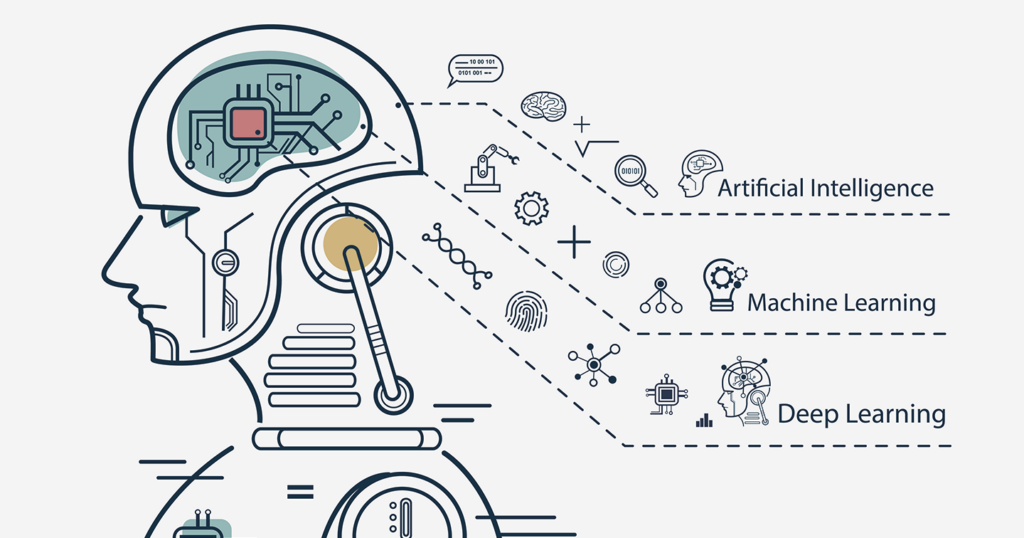
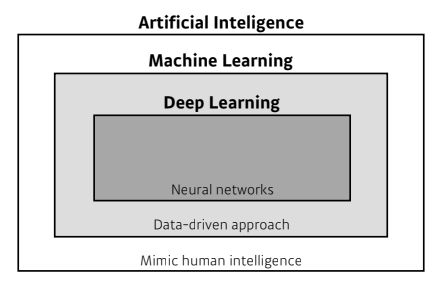
What is Deep Learning?
- AI: 기계 또는 컴퓨터 프로그램을 통해 인간을 모방하거나 복제하는 것
- ML: 인공지능의 한 분야로, 미리 정해둔 규칙 없이 다수의 데이터로부터 학습을 하고, 일반적인 규칙을 도출하는 것
- DL: 머신러닝의 한 분야로, 인공신경망을 기반으로 데이터를 학습하고, 일반적인 규칙을 도출하는 것
Key Components of Deep Learning
Data
- 풀고싶은 문제의 규칙을 도출하기 위해 필요한 데이터
- ex) 고양이와 강아지를 분류하고 싶으면, 고양이와 강아지에 대한 이미지가 필요함
Model
- 데이터를 어떤식으로 변형시켜서 학습하고, 원하는 값을 도출해낼지에 대한 방법들
- ex) 고양이와 강아지를 분류하고 싶을 때, 해당하는 이미지(input)가 고양이인지 혹은 강아지인지에 대한 label(output)이 나와야 됨. 이때 데이터를 어떻게 변형시킬 것인지에 대한 방법이 model임.
- AlexNet, GoogLeNet, ResNet, DenseNet, LSTM, GAN, ...
Loss Function
- 모델이 만들어낸 어떠한 값과 실제 정답의 간격(차이)을 어떻게 정의할 것인가?
- 모델을 학습시킨다는 것은 결국 loss를 최소화시키는 것임.
- ex) 회귀 예시
-
하이퍼파라미터 제안 값 입력 유닛의 수 특성의 수와 같아야 함 출력 유닛의 수 예측 변수의 개수와 같아야 함 은닉층의 활성화 함수 ReLU 추천 출력층의 활성화 함수 없음(범위 제한을 위해선 사용 가능) 비용(손실)함수 MSE(평균제곱합)
-
- ex) 분류 예시
-
하이퍼파라미터 이진 분류 다중 레이블 분류 다진 분류 입력층과 은닉층 회귀와 동일 회귀와 동일 회귀와 동일 출력 유닛의 수 1개 레이블마다 1개 클래스마다 1개 출력층의 활성화 함수 로지스틱 함수 로지스틱 함수 소프트맥스 함수 손실 함수 크로스 엔트로피 크로스 엔트로피 크로스 엔트로피 - 이진 분류 : 2개의 클래스 레이블
- 다중 레이블 분류 : ex) 스팸 여부와 긴급성 여부
- 다진 분류 : 3개 이상의 클래스 레이블
❗Loss function마다 성질은 다 다르고 경우에 따라서 오류를 일으킬 수 있음. 따라서 loss를 이해하고, 이를 적절히 이용할 수 있어야 함(위 예시는 '정해진 것'이 아님!)
-
algorithm
- loss를 최소화하기 위한 알고리즘들을 의미
- SGD, Momentum, Adagrad, ...
Multi-Layer Perceptron
Linear Neural Networks
- 간단헌 선형회귀모델을 먼저 살펴보자:
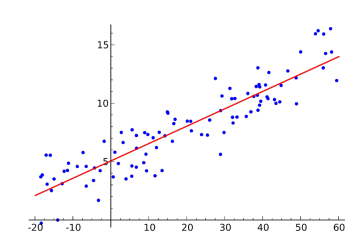
- 선형회귀모델에서는 라는 1차원 입력으로부터 라는 1차원 target을 가장 잘 표현할 수 있는 회귀직선을 그리는 것이 목적임
- Data:
- Model:
- Loss: (MSE)
- 최적의 w, b를 찾기 위해 우리는 예측값()과 실제값()의 손실을 최소화하는 가중치(파라미터)를 찾는 과정이 필요하다.
- 우리는 w, b를 각각 편미분하고,
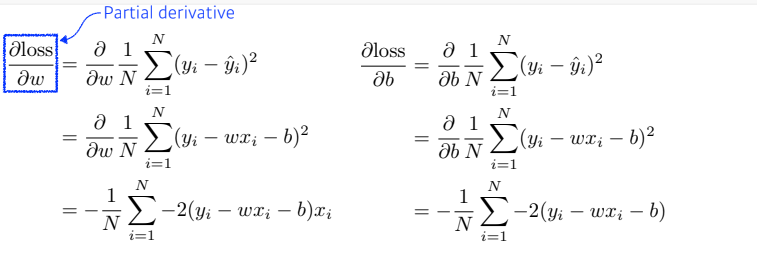
- 이를 w, b에 지속적으로 업데이트하여 이를 찾을 수 있다.
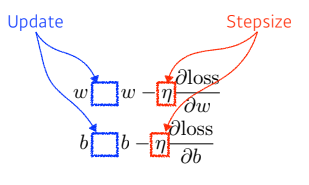
- 우리는 w, b를 각각 편미분하고,
- 이러한 과정은 다차원일 때도 동일하다. 우린 행렬을 벡터공간에서 연산자(operator)로 사용함으로써 벡터(x)를 다른 차원의 공간(y)으로 보낼 수 있다.
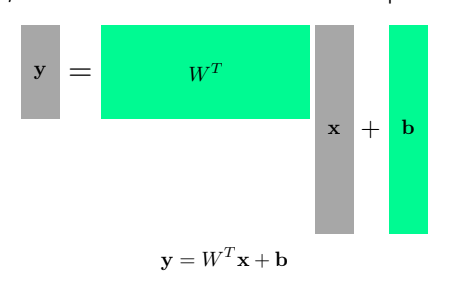
Beyond Linear Neural Networks
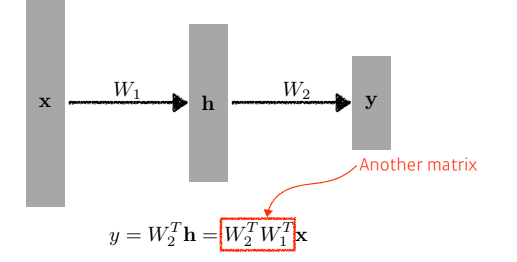
- 여기에서 가중치를 더 쌓는다면, 우린 더 많은 표현력을 가진 가중치를 얻을 수 있다.
- 하지만 단순히 가중치를 깊이만 쌓는 것은 결국 단순히 행렬곱을 늘리는 것과 다름 없으므로, 1단의 가중치와 다를 바가 없다.
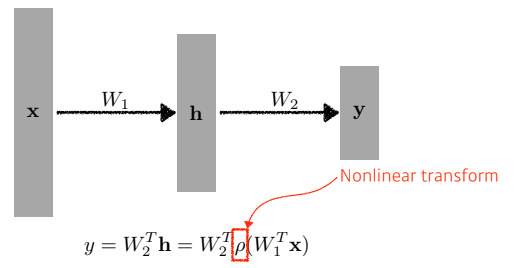
- 우리는 Nonlinear transform를 통해 이를 해결할 수 있고, 이러한 함수를 Activation Function이라고 한다.
- 대표적인 Activation Functions (wikipedia)
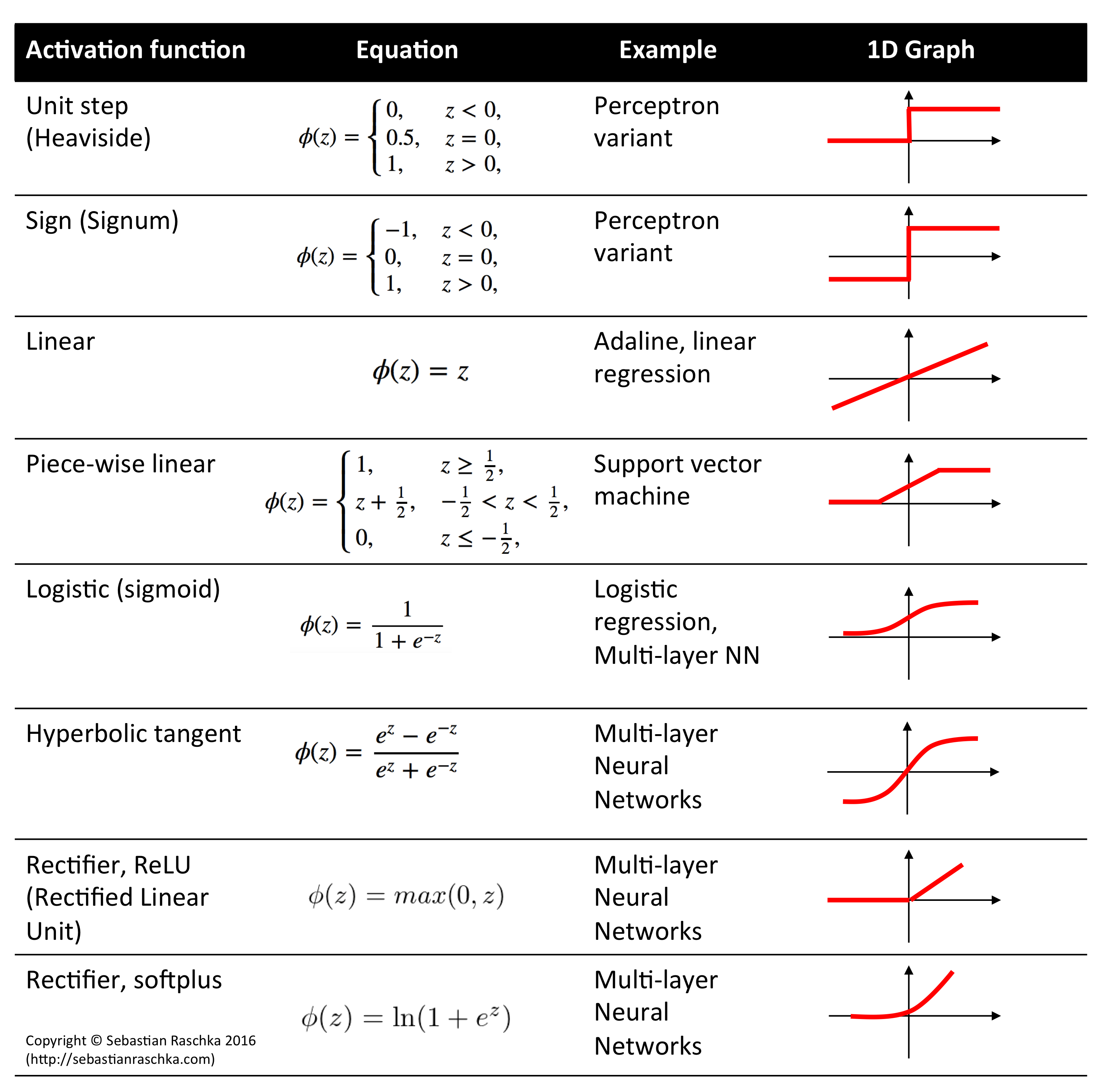
- 대표적인 Activation Functions (wikipedia)
- 하지만 단순히 가중치를 깊이만 쌓는 것은 결국 단순히 행렬곱을 늘리는 것과 다름 없으므로, 1단의 가중치와 다를 바가 없다.
