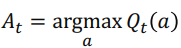
Multi-Armed Bandit

• MAB의 기본 원리

MAB란

Multi-Armed Bandit

• One-Armed Bandit
  : 게임장에 있는 슬롯머신은 한 번에 한 개의 arm을 당길 수 있음
  -> 게임장에 있는 k개의 슬롯머신을 N번 플레이 할 수 있다면?
• Multi-Armed Bandit
  : K개의 슬롯머신에서 얻을 수 있는 reward의 확률이 모두 다르다고 가정하고,
  제한된 횟수 N번 동안 K개의 슬롯머신을 어떤 순서대로 혹은 어떤 정책(policy)에 의해 돌려서 최대의 reward를 얻고자 하는 문제

MAB의 문제점과 정책

• 문제점: 슬롯머신의 reward 확률을 정확히 알 수 없음
  • 따라서,
    1. 각 슬롯머신의 reward 확률을 알아야 하며,
    2. 높은 reward를 가지는 슬롯머신을 최대한 활용해야 함.

    -> 그러나, Exploration & Exploitation는 Trade-off

• Exploration & Exploitation Trade-off
  • Exploration(탐색): 더 많은 정보를 얻기 위해 새로운 arm을 탐색
  • Exploitation(활용): 기존의 경험을 토대로 가장 좋은 arm을 선택
  • 탐색이 많고 & 활용이 적은 경우
    : 높은 reward를 얻을 수 없음
  • 탐색이 적고 & 활용이 많은 경우
    : 잘못된 슬롯머신을 활용하게 되면 높은 reward를 보장할 수 없음

  -> 적절한 policy를 만들어서 최대한 reward를 얻는 것이 MAB 알고리즘의 핵심!

MAB 문제 정의

MAB Formula

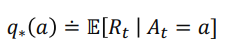
• $t$: time step(play num)
• $A_t$: 시간 t에 play한 action
• $R_t$: 시간 t에 play한 action을 통해 받은 reward
• $q_*(a)$: 액션 $\alpha$에 따른 reward의 실제 기대값

문제 정의

• 모든 action에 대한 $q_*(a)$를 모름
• 따라서 $q_*(a)$에 대한 시간 $t$에서의 추정치 $Q_t(a)$를 최대한 정밀하게 구하는 것이 목표임
  • 매번 추정 가치가 최대인 action을 선택하는 것을 greedy action이라 함
    • greedy action -> exploitation
    • 다른 action 선택 -> exploration

다양한 MAB 알고리즘 - 기초

Simple Average Greedy Algorithm

• 실제 기대값 $q_*(a)$의 가장 간단한 추정 방식으로 표본평균을 사용
  • ex) 지금까지 관측된 개별 머신의 Reward 평균값
• 가장 간단한 policy로, 평균 리워드가 최대인 action을 선택하는 것(greedy)
  • 
• 문제점: Exploration이 부족
  • 초반에 운이 안 좋게 낮은 reward가 구해졌다면,
    해당 action의 reward의 평균은 낮아지고, 앞으로 해당 action이 선택될 기회가 없어짐
    (초반 운이 중요하게 작용)

Epsilon-Greedy Algorithm

: Exploration이 부족한 greedy algorithm의 policy를 수정한 전략

• 일정 확률에 의해 랜덤으로 슬롯머신을 선택하도록 함
  
  • ex) 동전을 던져 앞면이 나오면 greedy(exploitation), 뒷면이 나오면 랜덤 선택(exploration)
  • $\epsilon$은 하이퍼파라미터임
• epsilon-greedy는 간단하면서도 exploration과 exploitation을 어느정도 보장하는 알고리즘임.
• 문제점: 어느정도 timestep이 많이 지나고, 데이터가 충분히 쌓여서 각각의 action의 true distribution이 충분히 수정이 됐음에도 불구하고 계속해서 탐색을 하기 때문에 후반에서는 비교적 손해를 많이 보는 알고리즘임.

Upper Confidence Bound (UCB)

• UCB formula
  
  • $Q_t(a)$: 시간 $t$에서 액션 $a$에 대한 reward 추정치(simple average)
  • $N_t(a)$: 지금까지의 관측값들 중에서 액션 $a$를 선택했던 횟수
  • $c$: exploration을 조정하는 하이퍼파라미터
• 불확실성 term은 해당 action이 최적의 action이 될 수도 있는 가능성(불확실성)을 표현
  • 모든 action이 충분히 탐색된 이후에는 $N_t(a)$의 값이 전반적으로 높아질 것이고, $ln$ $t$는 로그로 인해 증가폭이 줄어들기 때문에, 결국 0으로 수렴하게 됨(앞에 있는 Greedy term만을 사용하게 됨).

  -> 자연스럽게 exploration에서 exploitation으로 policy가 넘어가게 됨.

MAB알고리즘들과 하이퍼파라미터 튜닝

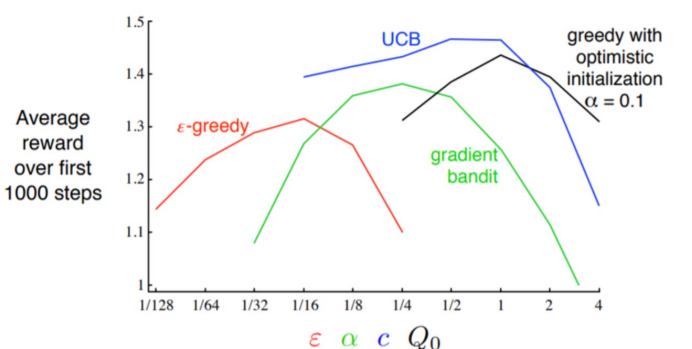
• 그림에서 알 수 있듯이 Exploration과 exploitation의 trade-off가 고려된 최적의 하이퍼파라미터를 찾아야 좋은 결과를 얻을 수 있음.

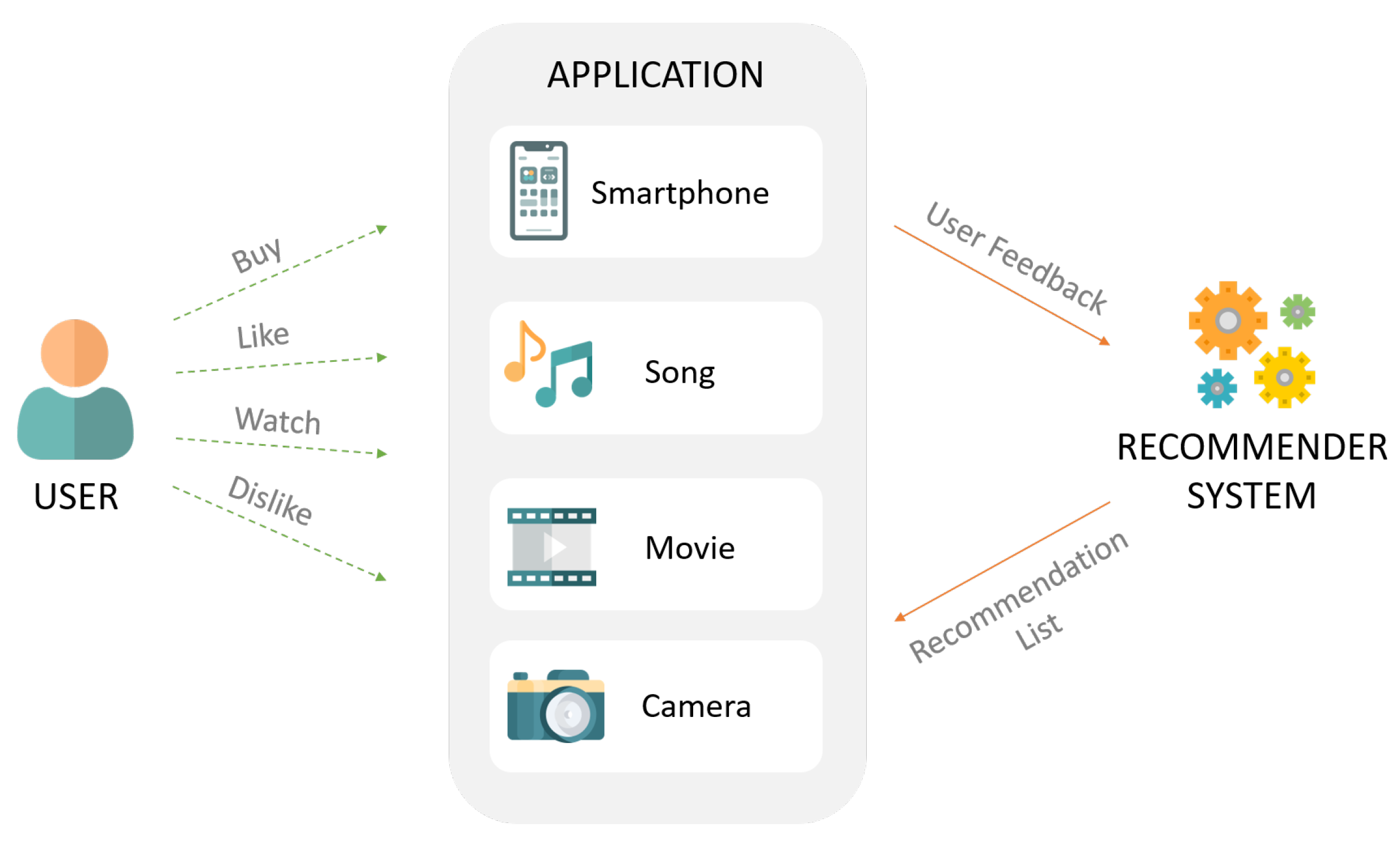
MAB를 이용한 추천시스템

• 추천시스템 문제를 Bandit 문제로 바꾼다면

  • 실제 서비스의 지표인 클릭/구매를 모델의 reward로 가정
    • Clicked = {0, 1}
  • 해당 reward가 최대화 되는 방향으로 모델이 학습되고 추천을 수행함

  -> 간단한 bandit 기법을 적용하여도 온라인 지표(CTR, CVR, ..)가 좋아짐

• 추천시스템에서의 exploration & exploitation

  • exploration: 지속적으로 변화하는 유저의 취향 탐색 및 추천아이템 확장
  • exploitation: 유저의 취향에 맞는 아이템 추천(개인화)

Bandit을 이용한 유저 추천

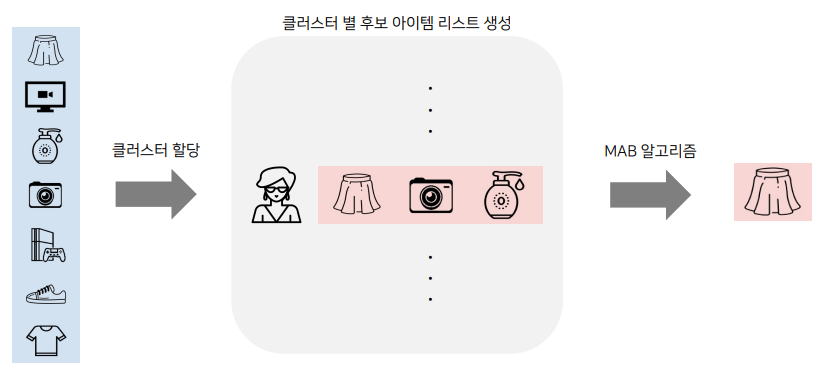
• 개별 유저에 대해 모든 아이템의 Bandit을 구하는 것은 불가능(데이터 부족 등)
• 클러스터링을 통해 비슷한 유저끼리 그룹화한 뒤, 해당 그룹 내에서 Bandit을 구축
  • 인기도 기반, CF 등의 기법을 통해 클러스터 별로 아이템 후보 리스트를 생성
  • 필요한 Bandit의 개수 = 유저 클러스터 수 * 후보 아이템 수

Bandit을 이용한 아이템 추천

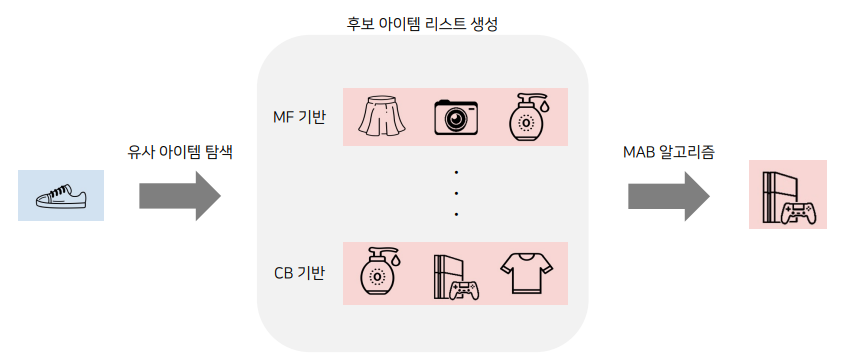
• 주어진 아이템과 유사한 후보 아이템 리스트를 생성하고, 그 안에서 Bandit을 적용
  • 필요한 Bandit의 개수 = 아이템 수 * 후보 아이템 수
• 유사한 아이템 추출 방법
  • MF 기반, Content-Based 기반, ...

다양한 MAB 알고리즘 - 심화

Thompson Sampling

: 주어진 k개의 action에 해당하는 확률분포를 구하는 문제

• action $a$에 해당하는 reward 추정치 $Q_t(a)$가 확률분포를 따른다고 가정(베타 분포)
• 베타 분포
  : 두 개의 양의 변수로 표현할 수 있는 확률 분포이며, 0과 1사이 값을 갖는다.
  
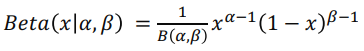
  • ($B(\alpha, \beta)$는 $\alpha, \beta$라는 하이퍼파라미터가 필요)

Thompson Sampling 예시

: 사용자에게 보여줄 수 있는 광고 배너가 있다고 가정

• 베타분포에 필요한 데이터는 2가지
  • 베너를 클릭한 횟수($\alpha$)
  • 베너를 클릭하지 않은 횟수($\beta$)
• 베너를 클릭할 확률 ~ $Beta(\alpha+1, \beta+1)$

배너	click ($\alpha)$	non-click ($\beta$)	표본평균
banner1	3	10	$\frac{3}{3+10}$
banner2	2	4	$\frac{2}{2+4}$
banner3	2	9	$\frac{1}{1+9}$

• 만약, Greedy라면 -> 표본 평균이 가장 높은 banner2만 계속해서 노출시킴
• 이와 다르게, Thompson Sampling은 각각의 banner가 가지고 있는 베타분포로부터 sampling한 값이 가장 높은 banner를 선택해서 노출시킴.

Thompson Sampling 과정

1. 데이터가 없는 초기 상태
   $\alpha = 0, \beta = 0$이므로, $Beta(1, 1)$
2. 데이터를 랜덤하게 노출
   • 이때, 클릭하면 $\alpha$ + 1, 클릭하지 않으면 $\beta + 1$
3. (2) (어느정도) 반복
4. 어느정도 분포가 형성되면, 베타분포에서 각자 샘플링
   • 추출된 샘플에서 가장 높은 확률의 베너를 노출
   • 이때, 클릭하면 $\alpha$ + 1, 클릭하지 않으면 $\beta + 1$
5. (3) 반복
   

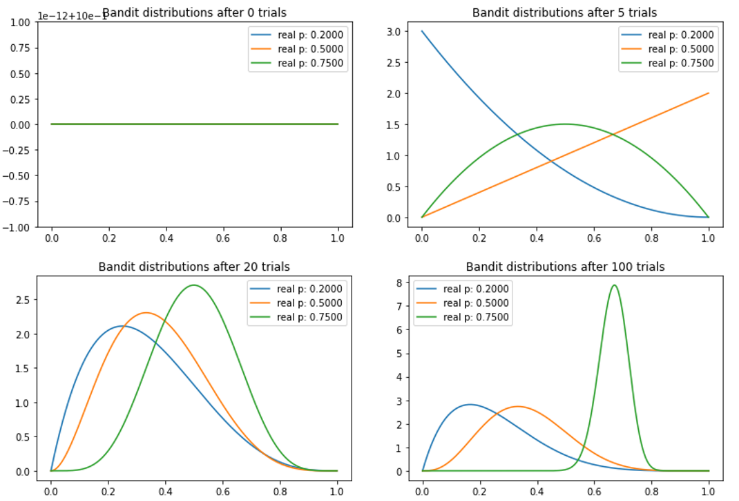
-> 수많은 노출을 거친 귀에는 베타분포가 굉장히 뾰족해지므로, 평균 CTR이 낮은 banner가 높은 CTR을 가진 banner보다 높게 샘플링될 확률은 거의 없어짐.

LinUCB

Contextual Bandit

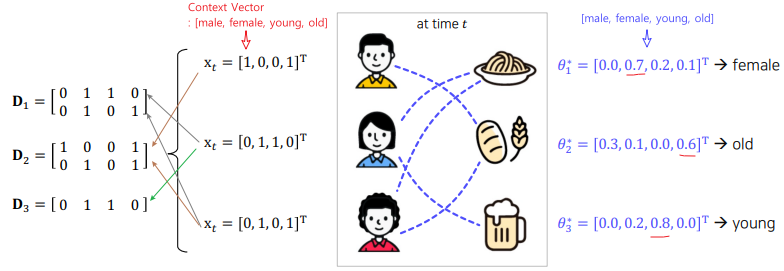
: 유저의 context 정보에 따라 동일한 action이더라도 다른 reward를 가진다고 가정

• ex) 동일한 스포츠 기사를 보더라도 나이 및 성별 등에 따라 클릭 성향이 다름(개인화)

Arm-selection Strategy

• $X_{t, a}$: d-차원 컨텍스트 벡터
  (user와 context에 대한 feature와 action(item)의 부가적인 정보가 포함)
  ($a$ -> action(item) 부가정보)
• $\theta^*_a$: action a에 대한 d-차원 학습 파라미터
• $D_a$: t시점의 m개의 컨텍스트 벡터(학습 데이터)로 구성된 (m*d) 행
  • m개의 컨텍스트 벡터 == m개의 관측된 액션 데이터

LinUCB 예시

LinUCB Pseudo Code