기초 알고리즘 정리

whatSup CheatSheet·2022년 1월 17일

나동빈님의 이코테2021과 잔재미코딩님의 블로그 강의내용을 바탕으로 공부한 기초 알고리즘 이론들을 정리한 글입니다.

O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(2n) < O(n!)
요구사항에 따라 적절한 알고리즘 설계하기(시간제한 1초 기준)
- N의 범위가 500인 경우: $O(N^3)$ 인 알고리즘을 설계하면 풀 수 있음
- N의 범위가 2,000인 경우: $O(N^2)$
- N의 범위가 100,000인 경우: $O(NlogN)$
- N의 범위가 10,000,000인 경우: $O(N)$

# map()
a = ['1', '2', '3', '4', '5']
a_map = list(map(int, a))
a_map

[1, 2, 3, 4, 5]

자주 사용되는 표준 라이브러리

itertolls: 파이썬에서 반복되는 형태의 데이터를 처리하기 위한 유용한 기능들을 제공
- 순열(P)과 조합(C) 라이브러리는 코딩 테스트에서 자주 사용됨
  - 순열: 서로 다른 n개에서 서로 다른 r개를 선택하여 일렬로 나열하는 것 $n$ P $r$
    - $_9P_6 = \frac{9!}{(9-6!)}$
  - 조합: 서로 다른 n개에서 순서에 상관 없이 서로 다른 r개를 선택한는 것 $n$ C $r$
    - $_9C_6 = \frac{_9P_6}{6!}$
heapq: 힙(heap) 자료구조를 제공
- 일반적으로 우선순위 큐 기능을 구현하기 위해 사용됨
bisect: 이진 탐색 기능을 제공
collections: 덱(deque), 카운터(counter) 등의 유용한 자료구조를 포함
math: 팩토리얼, 제곱근, 최대공약수, 삼각함수, 파이 등
- math.ceil() : 실수 올림
- math.floor() : 실수 내림

자주 사용되는 내장함수 & 알고리즘

eval()

result =  eval("3 + 4 * 7")
result

sorted() with key

l = [['홍길동', 35], ['이순신', 75], ['아무개', 50]]
print(l)

l.sort(key = lambda x: x[1], reverse = True)
print(l)

[['홍길동', 35], ['이순신', 75], ['아무개', 50]]
[['이순신', 75], ['아무개', 50], ['홍길동', 35]]

배열 2차원 배열 동시에 sort

l = [['홍길동', 35], ['이순신', 75], ['아무개', 80]]
print(l)

l.sort(key = lambda x: (x[0], x[1])) # 0번쨰 -> 1번째
print(l)

[['홍길동', 35], ['이순신', 75], ['아무개', 80]]
[['아무개', 80], ['이순신', 75], ['홍길동', 35]]

진수 변환법
- 2진수: bin()
- 8진수: oct()
- 16진수: hex()
  -> 10진수: int를 받아, 해당하는 진수: str로 반환됨

# 모든 진수 변환
def converter(num, b):
    '''자연수(num)를 b진수로 변환'''
    tmp = ''
    while num:
        tmp += str(num % b) 
        num = num // b  
    
    return tmp[::-1]
    
>> print(converter(45, 3))

# n진수를 10진수로 변환
int(tmp[::-1], 3)  # 3진수 -> 10진수

소수 구하기

# 에라토스테네스의 체
def solution(n):
    answer = 0
    t_f = [False, False] + [True for _ in range(2, n + 1)]
    for i in range(2, n + 1):
        if t_f[i]:
            answer +=1
            for j in range(i * i, n + 1, i):
                t_f[j] = False
    return answer
    
solution(1000000)

# 소수 판별(제곱근)
import math

def is_prime(n):
	# n의 제곱근을 정수화 시켜준 후 + 1
    for i in range(2, int(math.sqrt(n))+1): 
        if n % i == 0:
            return False

    return True

itertools

순열, 조합

from itertools import permutations

data = ['a', 'b', 'c']

result = list(permutations(data, 2))    # 3개
print(result)

[('a', 'b'), ('a', 'c'), ('b', 'a'), ('b', 'c'), ('c', 'a'), ('c', 'b')]

from itertools import combinations

data = ['a', 'b', 'c']

result = list(combinations(data, 2))    # 2개
print(result)

[('a', 'b'), ('a', 'c'), ('b', 'c')]

중복 순열과 중복 조합

# product1
from itertools import product

data = ['a', 'b', 'c']

result = list(product(data, repeat = 2))
print(result)

[('a', 'a'), ('a', 'b'), ('a', 'c'), ('b', 'a'), ('b', 'b'), ('b', 'c'), ('c', 'a'), ('c', 'b'), ('c', 'c')]

# product2
from itertools import product
l = ['ab', '12']
s = list(product(*l))
s

[('a', '1'), ('a', '2'), ('b', '1'), ('b', '2')]

#combinations_with_replacement
from itertools import combinations_with_replacement

data = ['a', 'b', 'c']

result = list(combinations_with_replacement(data, 2))
print(result)

[('a', 'a'), ('a', 'b'), ('a', 'c'), ('b', 'b'), ('b', 'c'), ('c', 'c')]

collectios.Counter

리스트와 같이 반복 가능한(iterable) 객체가 주어졌을 때 내부의 원소가 몇 번씩 등장하는지 알려줌

from collections import Counter

counter = Counter(['red', 'blue', 'red', 'green', 'blue', 'blue'])

print(counter['red'])  # 'blue'가 등장한 횟수
print(dict(counter))  # 사전 형태로 반환

2
{'red': 2, 'blue': 3, 'green': 1}

최대 공약수와 최소 공배수

math 라이브러리의 gcd(): 최대 공약수 계산

import math

# 최소 공배수를 구하는 함수
def lcm(a, b):
    return a * b // math.gcd(a, b)

print(math.gcd(21, 14))  # 최대 공약수(GCD)
print(lcm(21, 14))  # 최소 공배수(LCM)

7
42

heapq(우선순위 큐)

파이썬 heapq는 최소 힙으로 구현되어 있음
최대 힙은 heappush 시 -1을 곱해주고, 출력 시 -1를 다시 곱해주면 됨.

import heapq

queue = []

heapq.heappush(queue, [2, 'A'])
heapq.heappush(queue, [5, 'B'])
heapq.heappush(queue, [1, 'C'])
heapq.heappush(queue, [7, 'D'])
print(queue)
for i in range(len(queue)):
    print(heapq.heappop(queue))

[[1, 'C'], [5, 'B'], [2, 'A'], [7, 'D']]
[1, 'C']
[2, 'A']
[5, 'B']
[7, 'D']

# heapify
import heapq

queue = [[2, 'A'], [5, 'B'], [1, 'C'], [7, 'D']]
heapq.heapify(queue)
print(queue)
for i in range(len(queue)):
    print(heapq.heappop(queue))

[[1, 'C'], [5, 'B'], [2, 'A'], [7, 'D']]
[1, 'C']
[2, 'A']
[5, 'B']
[7, 'D']

리스트

.remove(num)
.index(num)
del list[index]
.insert(index, num)
.count(num)
.reverse()
reversed()

a = [2, 5, 6, 78, 2, 3, 54, 6, 1]

a.remove(78)
print(a)

print(a.index(54))

del a[0]
print(a)

a.insert(2, 999)
print(a)

print(a.count(6))

a.reverse()
print(a)

print(list(reversed(a)))

[2, 5, 6, 2, 3, 54, 6, 1]

5

[5, 6, 2, 3, 54, 6, 1]

[5, 6, 999, 2, 3, 54, 6, 1]

2

[1, 6, 54, 3, 2, 999, 6, 5]

[5, 6, 999, 2, 3, 54, 6, 1]

2차원 리스트의 총 합 구하기

arr = [[1, 1, 0, 0], [1, 0, 0, 0], [1, 0, 0, 1], [1, 1, 1, 1]]
print(sum(sum(arr, [])))

# 9 출력됨

세트

{} or set()
.add(x) : 세트에 요소를 추가
.remove(x) : 특정 요소를 삭제하고, 없으면 에러 발생시킴
.discard(x) : 특정 요소를 삭제하고, 없으면 그냥 넘어감
pop, clear, len, copy

딕셔너리

.get(key, 대체) : key의 value를 가져온다. key가 존재하지 않을 경우 '대체'를 출력한다.

a = dict()
a.get('hello', 'ws')

'ws'

최대값, 최소값

a = {4:2, 2:6, 5:3, 7:1, 1:20, 4:3}
a

{4: 3, 2: 6, 5: 3, 7: 1, 1: 20}

max(a)  # keys 중 가장 큰 값

max(a, key = a.get)  # values 중 가장 큰 값을 가진 key

dict.pop(key) : key의 value를 pop 한다

print(a.pop(5))
print(a)

3
{4: 3, 2: 6, 7: 1, 1: 20}

key, value 서로 스왑

dic = dict(zip('abcde', range(5)))
dic_swap = {v:k for k,v in dic.items()}

Counter.defaultdict
- key가 없을시 default를 정해줌

from collections import defaultdict

d = defaultdict(lambda : 100)

d['hello'] = 1
print(d['hello'])
print(d['hi'])

1
100

defaultdict(<function __main__.<lambda>()>, {'hello': 1, 'hi': 100})

할당

배운점

(아래 코드)반복문 속에서 append 할 때 주소가 now_h 객체를 가르키기 때문에 queue에 있는 모든 값들이 다 함께 변경 됨.
```
    now_h[0] += dr[d_now % 4]
    now_h[1] += dc[d_now % 4]
    queue.append(now_h)
```

아래 코드처럼 해야 제대로된 queue가 뙴

    now_h[0] += dr[d_now % 4]
    now_h[1] += dc[d_now % 4]
    queue.append([now_h[0], now_h[1]])

a = [1, 2, 3]
b = list()
for i in range(3):
    b.append(a)
    a[1] += 1
b

[[1, 5, 3], [1, 5, 3], [1, 5, 3]]

a = [1, 2, 3]
b = list()
for i in range(3):
    b.append([a[0], a[1], a[2]])
    a[1] += 1
b

[[1, 2, 3], [1, 3, 3], [1, 4, 3]]

# 얕은 복사 사용
a = [1, 2, 3]
b = list()
for i in range(3):
    b.append(a.copy())
    a[1] += 1
b

[[1, 2, 3], [1, 3, 3], [1, 4, 3]]

얕은 복사와 깊은 복사

얕은 복사(.copy())
- mutable한 객체는 얕은 복사를 하면 새로운 주소값을 할당 받는다.
- 하지만 2차원 이상의 mutable 객체에서 안에 들어있는 각각의 객체들은,
  - 겉에 있는 객체(복사한 새로운 객체)가 새로운 주소값을 할당받는다 해도 그 안에 있는 각각의 mutable한 객체는 기존 객체의 안에 있는 각각의 mutable한 객체를 가리키고 있기 때문에
  - 복사한 새로운 객체의 값을 바꾸면 기존 객체의 요소들도 변경된다
이를 보완한 것이 깊은복사
1. copy 라이브러리 이용
- import copy
- new_obj = copy.deepcopy(기존 객체)
1. 2차원 리스트일 때 슬라이싱 이용(1.5배 이상 더 빠름)
- new_obj = [i[:] for i in 기존 리스트]

문자열

대/소문자 변환

.upper() : 모든 문자 변환
.lower() : 모든 문자 변환
.title() : 각 단어의 첫 글자만 대문자, 나머지는 소문자
.capitalize : 첫 글자만 대문자, 나머지는 소문자

문자열 탐색

.find('a') : 찾으면 인덱스 반환, 못찾으면 -1 반환
.index('a') : 찾으면 인덱스 반환, 못찾으면 오류 발생
.count('a', 3) : 특정 문자의 개수 반환(두번째 인자는 시작 인덱스를 의미)

문자열 구성

.isdigit() : 숫자로만 구성되어있는지
.isalpha() : 알파벳으로만 구성되어있는지(한글 포함)
.isupper() : 모두 대문자인지(숫자, 공백은 상관x)
.islower() : 모두 소문자인지(숫자, 공백은 상관x)

공백제거, 대체

(줄바꿈\n 이나 tab\t도 제거가 가능)

.strip() : 양쪽 끝 공백을 제거
.rstrip() : 오른쪽 끝 공백 제거
.lstrip() : 왼쪽 끝 공백 제거
.replace(a, b, n) : a문자를 b로 교체(n번 limit, limit가 없으면 전부 교체)

쪼개기, 합치기

.split() : 문자열 쪼개기
' '.join(문자열 리스트) : ' '을 사이에 끼고 합치기

포맷팅

f-string(python 3.6~) : 새로운 파이썬 포맷팅
- 정수끼리 산술연산도 지원
- 속도면에서도 가장 빠름

name = 'bob'
test = f'Hello {name}'  # f ~~
print(test)

Hello bob

a, b = 2, 3
test = f'합: {a + b}'  # f ~~
print(test)

합: 5

# f-string 선언을 먼저 해도 됨
test = f'합: {a + b}'  # f ~~
a, b = 2, 3
print(test)

합: 5

정규표현식

참고자료

정규표현식에서 사용되는 메타 문자들

문자 클래스 [ ] : "[ ]사이의 문자들과 매치”를 의미
하이픈 - : 두 문자 사이의 범위(From - To)를 의미
- [a-zA-Z] : 알파벳 모두
- [0-9] : 숫자 모두 == \d
^ : 반대(not)를 의미
- \D == [^0-9] → 숫자가 아닌 것들을 의미
Dot . : 줄바꿈 문자인 \n을 제외한 모든 문자와 매치됨을 의미
- ex) a.b : “a+모든문자+b”
- ex) a[.]b : 정확히 “a.b”를 의미
반복 * : * 바로 앞에 있는 문자가 0부터 무한대로 반복될 수 있다는 의미
- ex) 정규식이 ca*t 일 때,
  - “ct” : a가 0번 반복 → True
  - “cat” : a가 1번 반복 → True
  - “caat” : a가 2번 반복 → True
반복 + : + 바로 앞에 있는 문자가 1부터 무한대로 반복될 수 있다는 의미(*은 0부터)
반복 {m,n} **:** m부터 n까지 반복 횟수가 고정적인 것을 찾음
- ex) ca{2}t
  - “cat” : False
  - “catt” : True
- ex) ca{2, 5}t
  - “cat” : False
  - “caaaat” : True
? : 바로 앞 글자가 있어도 되고, 없어도 됨을 의미
- ex) ca?t : “cat”, “ct” → True

파이썬 re 모듈

match() : 문자열의 처음부터 정규식과 매치되는지 조사

import re
p = re.compile('[a-z]+')
m1 = p.match("python")
m2 = p.match("3 python")
print(m1)
print(m2)

# 하단은 출력
<re.Match object; span=(0, 6), match='python'>  # Match 객체를 돌려줌
None  # None을 돌려줌

search() : 문자열 전체를 검색하여 정규식과 매치되는지 조사

import re
p = re.compile('[a-z]+')
m2 = p.search("3 python")
print(m2)

# 하단은 출력
<re.Match object; span=(2, 8), match='python'>  # 매치되는 부분을 찾아서 돌려줌

findall() : 정규식과 매치되는 모든 문자열을 리스트로 돌려줌

import re
p = re.compile('[a-z]+')

result = p.findall("life is too short")
print(result)

# 하단은 출력
['life', 'is', 'too', 'short']

finditer() : 정규식과 매치되는 모든 문자열을 반복 가능한 객체로 돌려줌

import re
p = re.compile('[a-z]+')

result = p.finditer("life is too short")
print(result)

# 하단은 출력
<callable_iterator object at 0x01F5E390>

for r in result: print(r)

# 하단은 출력
# match 객체로 출력됨
<re.Match object; span=(0, 4), match='life'>
<re.Match object; span=(5, 7), match='is'>
<re.Match object; span=(8, 11), match='too'>
<re.Match object; span=(12, 17), match='short'>

match 객체
- .group() : 매치된 문자열을 반환
- .start() : 매치된 문자열의 시작 위치를 반환
- .end() : 매치된 문자열의 끝 위치를 반환
- .span() : 매치된 문자열의 (시작, 끝) 을 튜플로 반환

파이썬 컴프리핸션

# if
[i for i in range(1, 11) if i % 2 == 0]  # 짝수만

[2, 4, 6, 8, 10]

# if ~ else
[i if i % 2 == 0 else 'No' for i in range(1, 11)]

['No', 2, 'No', 4, 'No', 6, 'No', 8, 'No', 10]

chr

ord(): 아스키 코드로, chr() : 문자로

파이썬 Nonlocal, global

# 참고: https://www.daleseo.com/python-global-nonlocal/

global_var = "전역 변수"
def outer():
    nonlocal_var = "비전역 변수"
    print(global_var) # 가능
    print(nonlocal_var) # 가능

    def inner():
        local_var = "지역 변수"
        print(global_var) # 가능
        print(nonlocal_var) # 가능
        print(local_var) # 가능

time.timedelta

시간(날짜)로 연산을 할 수 있음
datetime.timedelta(days=0, seconds=0, microseconds=0, milliseconds=0, minutes=0, hours=0, weeks=0)

from datetime import timedelta


delta1 = timedelta(seconds=57)
delta2 = timedelta(hours=25, seconds=2)  # minutes
print(delta2 != delta1)  # 출력 : True

d = delta1 - delta2
print(d)  # 출력 : 1 day, 0:59:05
print(d.total_seconds())  # 출력 : 89945.0 -> 초 단위(float)로 바꿔줌

그리디(greedy) 알고리즘

정당성 분석이 중요
- ex) 거스름 돈 문제 - 500원, 100원, 50원, 10원으로 가장 적은 동전수를 거슬러줘야 하는 문제
  - 가지고 있는 동전 중에서는 큰 단위가 항상 작은 단위의 배수이므로 작은 단위의 동전들을 종합해 다른 해가 나올 수 없기 때문에 가능함.
  - 만약, 800원을 거슬러 주는데 화폐 단위가 500원, 400원, 100원이었다면? --> 400원 * 2 가 최적의 해
  - 시간 복잡도: 동전의 종류만큼 반복. 따라서 O(N)

구현(Implementation)

구현이란 머릿속에 있는 알고리즘을 소스코드로 바꾸는 과정
구형 유형 문제: 풀이를 떠올리는 것은 쉽지만 소스코드로 옮기기 어려운 문제(시뮬레이션 등)
시뮬레이션 및 완전 탐색 문제에서는 2차원 공간에서의 방향 벡터가 자주 활용됨

simul = list()
for i in range(5):
    simul.append([])
    for j in range(5):
        simul[i].append([i, j])
        
simul

[[[0, 0], [0, 1], [0, 2], [0, 3], [0, 4]],
 [[1, 0], [1, 1], [1, 2], [1, 3], [1, 4]],
 [[2, 0], [2, 1], [2, 2], [2, 3], [2, 4]],
 [[3, 0], [3, 1], [3, 2], [3, 3], [3, 4]],
 [[4, 0], [4, 1], [4, 2], [4, 3], [4, 4]]]

# 방향백터[동, 북, 서, 남] - 그래프가 아닌 행렬로 생각해야됨
# 현재 위치가 (2, 2)일 때 - 행, 열
x, y = 2, 2
dx = [0, -1, 0, 1]
dy = [1, 0, -1, 0]


# 상, 하, 좌, 우를 다 살펴보고자 할 떄 로직
for i in range(4):
    nx = x + dx[i]
    ny = y + dy[i]
    print(nx, ny)

그래프 탐색 알고리즘: DFS/BFS

깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS) 활용한 문제 유형/응용
1. 그래프의 모든 정점을 방문하는 것이 주요한 문제
  - 단순히 모든 정점을 방문하는 것이 중요한 문제의 경우 DFS, BFS 두 가지 방법 중 어느 것을 사용하셔도 상관없음
2. 경로의 특징을 저장해둬야 하는 문제
  - 예를 들면 각 정점에 숫자가 적혀있고 a부터 b까지 가는 경로를 구하는데 경로에 같은 숫자가 있으면 안 된다는 문제 등, 각각의 경로마다 특징을 저장해둬야 할 때는 DFS를 사용함. (BFS는 경로의 특징을 가지지 못함)
3. 최단거리 구해야 하는 문제
  - 미로 찾기 등 최단거리를 구해야 할 경우, BFS가 유리함.(깊이 우선 탐색으로 경로를 검색할 경우 처음으로 발견되는 해답이 최단거리가 아닐 수 있지만, 너비 우선 탐색으로 현재 노드에서 가까운 곳부터 찾기 때문에 경로를 탐색 시 먼저 찾아지는 해답이 곧 최단거리기 때문.
4. 이밖에도
  - 검색 대상 그래프가 정말 크다면 DFS를 고려
  - 재귀 사용시 DFS
  - 검색대상의 규모가 크지 않고, 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않다면 BFS

스택과 큐

스택

입구와 출구가 동일한 형태
- 파이썬 list 사용
- list.append()
  - 시간 복잡도 = O(1)
- list.pop()
  - 시간 복잡도 = O(1)

stack = []
stack.append(1)
stack.append(2)
stack.append(3)
stack.pop()
stack.append(4)
stack.append(5)
stack[::-1]

[5, 4, 2, 1]

큐

선입선출
- deque 라이브러리 사용

from collections import deque

queue = deque()
queue.append(1)
queue.append(2)
queue.append(3)
queue.popleft()
queue.append(4)
queue.append(5)
print(queue)

queue.reverse()  # 역순으로 바꾸기
print(queue)

queue.rotate(1)  # 로테이션 -> 
print(queue)

queue.extendleft([1, 2])  # extedleft
print(queue)

deque([2, 3, 4, 5])
deque([5, 4, 3, 2])
deque([2, 5, 4, 3])
deque([2, 1, 2, 5, 4, 3])

재귀함수

자기 자신을 다시 호출(종료 조건 신경쓰기)
파이썬에선 최대 깊이 제한이 있음
모든 재귀 함수는 반복문을 이용하여 동일한 기능을 구현할 수 있음
컴퓨터가 함수를 연속적으로 호출하면 컴퓨터 메모리 내부의 스택 프레임에 쌓임
- 이를 이용하여 스택 라이브러리 대신 재귀 함수를 이용하는 경우가 많음(DFS)
유클리드 호제법
- 두 자연수 A, B에 대하여(A > B)A를 B로 나눈 나머지를 R이라고 한다.
- 이때 A와 B의 최대공약수는 B와 R의 최대 공약수와 같다.
|단계|A|B|
|:--:|:--:|:--:|
|1|192|162|
|2|162|39|
|3|30|12|
|4|12|6|
- 192와 162의 최대 공약수는 12와 6의 최대공약수와 같다.
- 12는 6의 배수이기 때문에 6이 최대공약수

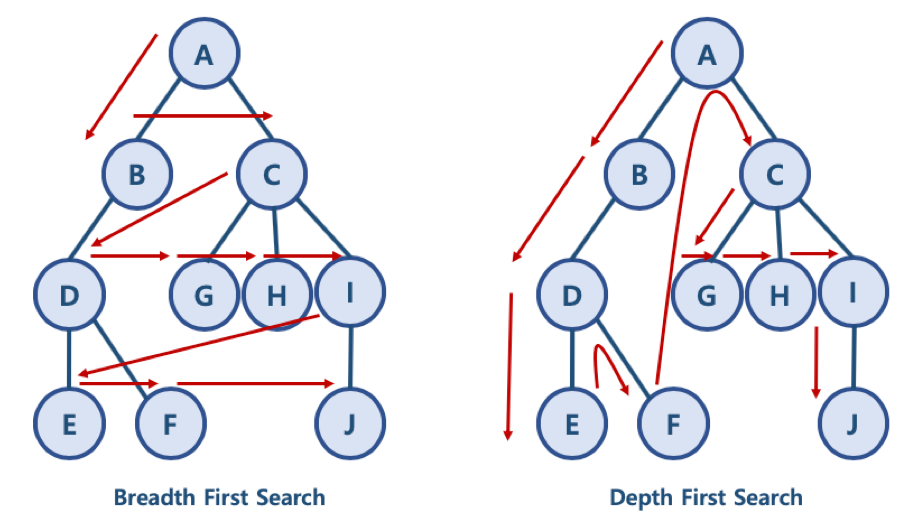
DFS(깊이 우선 탐색)

DFS는 스택 자료구조(혹은 재귀함수)를 이용한다.
DFS 동작 과정
1. 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
2. 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문처리한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
3. 더 이상 2번의 과정을 수행할 수 없을 때까지 반복

# 노드 정보
graph = [
    [], # 0번 인덱스는 비워둠
    [2, 3, 8],  # 1번 노드
    [1, 7],  # 2번 노드
    [1, 4, 5],  # 3번 노드
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7] # 8번 노드
]

visited = [False] * 9

# 반복
def dfs1(graph, start_node):
    visited, need_visit = list(), list()
    need_visit.append(start_node) 
    
    while need_visit:
        node = need_visit.pop() # 스택 
        if node not in visited: 
            visited.append(node)  
            need_visit.extend(graph[node])  # 스택
                                            # extend는 iterable 객체만 올 수 있음. 각 요소를 분리하여 끝에 삽입.
                                            # append였다면, 각 요소를 분리하지 않고 iterable 객체를 그대로 넣었음(2차원 형태)
    return visited

# 재귀
def dfs2(graph, v, visited):
    # 현재 노드 방문처리
    visited[v] = True
    print(v, end = ' ')
    
    for i in graph[v]:
        if not visited[i]:
            dfs2(graph, i, visited)

# 출력
print(dfs1(graph, 1))
print()
print(dfs2(graph, 1, visited))

[1, 8, 7, 6, 2, 3, 5, 4]

1 2 7 6 8 3 4 5 None

BFS(너비 우선 탐색)

BFS는 큐 자료구조를 이용한다.
시작 노드에서 가까운 노드들부터 방문
구체적인 동작 과정은 다음과 같다
1. 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
2. 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중 방문하지 않은 노드를 모두 큐에 삽입하고 방문처리한다.
3. 더 이상 2번의 과정을 수행할 수 없을 떄까지 반복

# 노드 정보
graph = [
    [], # 0번 인덱스는 비워둠
    [2, 3, 8],  # 1번 노드
    [1, 7],  # 2번 노드
    [1, 4, 5],  # 3번 노드
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7] # 8번 노드
]

visited = [False] * 9

#1
def bfs1(graph, start_node):
    visited, need_visit = list(), list()
    
    need_visit.append(start_node)
    
    while need_visit:
        node = need_visit.pop(0) # 큐.   (스택이면 DFS)
        if node not in visited:
            visited.append(node)
            need_visit.extend(graph[node])
    
    return visited

#2
from collections import deque

def bfs2(graph, start, visited):
    queue = deque([start])
    visited[start] = True
    
    while queue:
        v = queue.popleft()
        print(v, end = ' ')
        
        for i in graph[v]:
            if not visited[i]:
                queue.append(i)
                visited[i] = True

print(bfs1(graph, 1))
print(bfs2(graph, 1, visited))

[1, 2, 3, 8, 7, 4, 5, 6]
1 2 3 8 7 4 5 6 None

주의

들린 곳을 체크할 땐 꼭 need_visit에 append 하는 곳에서 할 것(시간 초과)

정렬 알고리즘

정렬: 데이터를 특정한 기준에 따라 순서대로 나열하는 것
일반적으로 문제 상황에 따라서 적절한 정렬 알고리즘이 공식처럼 사용됨

정렬 알고리즘	평균 시간 복잡도	공간 복잡도	특징
선택 정렬	O(N2)	O(N)	아이디어가 매우 간단함 (,,)
삽입 정렬	O(N2)	O(N)	데이터가 거의 정렬되어 있을 땐 가장 빠름
퀵 정렬	O(NlogN)	O(N)	대부분의 경우에 가장 접합하며, 충분히 빠름
계수 정렬	O(N+K)	O(N+K)	데이터의 크기가 한정되어 있는 경우에만 사용이 가능하지만 매우 빠르게 동작함

선택(Selection) 정렬

처리되지 않은 데이터 중에서 가장 작은 데이터를 선택해 맨 앞에 있는 데이터와 바꾸는 것을 반복
- 탐색 범위는 반복할 때마다 1개씩 줄어듦
- 맨 마지막은 안 해도 됨
시간복잡도: $O(N^2)$

array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

for i in range(len(array)):
    min_index = i
    for j in range(i + 1, len(array)):
        if array[min_index] > array[j]:
            min_index = j
    array[i], array[min_index] = array[min_index], array[i]  # 스왑

print(array)

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

삽입(Insert) 정렬

처리되지 않은 데이터를 하나씩 골라 적절한 위치에 삽입
선택 정렬에 비해 구현 난이도가 높은 편이지만, 일반적으로 더 효율적으로 동작함
시간복잡도: $O(N^2)$
- 삽입 정렬은 현재 리스트의 데이터가 거의 정렬되어 있는 상태라면 매우 빠르게 동작합
  - 최선의 경우(데이터가 다 정렬되어 있는 경우) $O(N)$

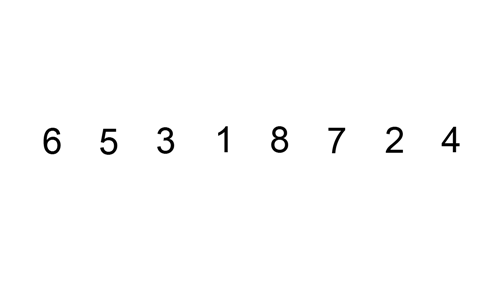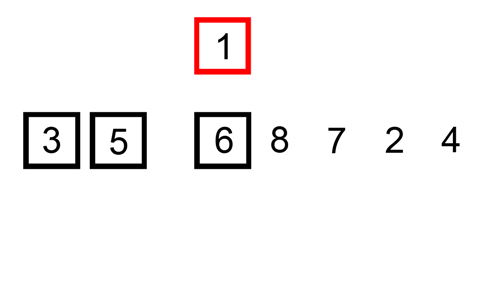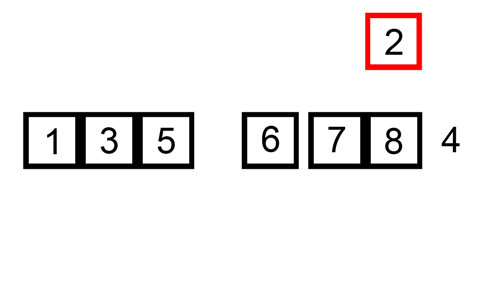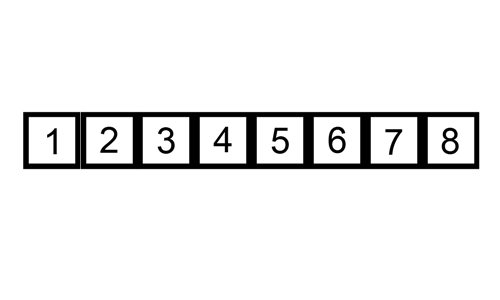
array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

for i in range(1, len(array)):
    for j in range(i, 0, -1): 
        if array[j] < array[j - 1]:
            array[j], array[j - 1] = array[j - 1], array[j]
        else:
            break
            
print(array)

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

퀵(Quick) 정렬

기준 데이터를 설정하고 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾸는 방법
일반적인 상황에서 가장 많이 사용되는 정렬 알고리즘 중 하나
가장 기본적인 퀸 정렬은 첫 번째 데이터를 기준 데이터(Pivot)로 설정함
시간복잡도: 퀵 정렬은 평균의 경우 $O(NlogN)$ 의 시간 복잡도를 가짐
- 최악의 경우 $O(N^2)$ 의 시간복잡도를 가짐(분할이 잘 안되는 경우, (이미 정렬된 배열에 대해 퀵 정렬))
퀵 정렬 동작 예시
- 왼쪽으로부터 pivot보다 큰 값을 찾고, 오른쪽으로부터 pivot보다 작은 값을 찾아서 스왑
- 위치가 엇갈리는 경우 pivot과 왼쪽 데이터(오른쪽에서 오던)의 위치를 서로 변경

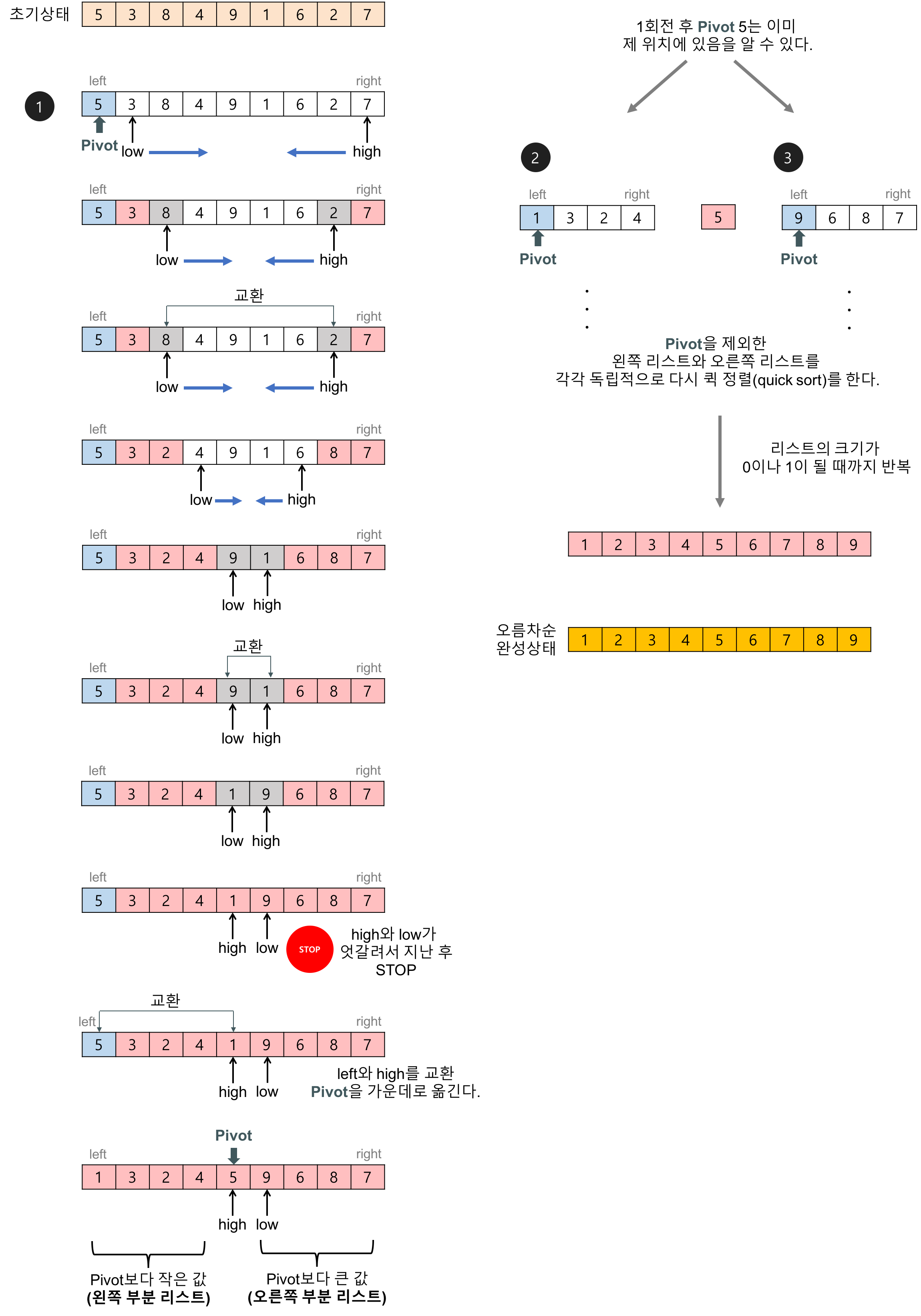
array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]

def quick_sort(array, start, end):
    if start >= end:  # 원소가 1개인 경우 종료
        return
    pivot = start # 피벗 설정
    left = start + 1
    right = end
    
    while(left <= right):
        # 피벗보다 큰 데이터를 찾을 떄까지 반복
        while(left <= end and array[left] <= array[pivot]):
            left += 1
        # 피벗보다 작은 데이터를 찾을 때까지 반복
        while(right > start and array[right] >= array[pivot]):
            right -= 1
        # 엇갈렸다면, 작은 데이터와 피벗을 교체
        if(left > right):
            array[right], array[pivot] = array[pivot], array[right]
        # 엇갈리지 않았다면 작은 데이터와 큰 데이터를 교체
        else:
            array[left], array[right] = array[right], array[left]
    
    # 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬 수행
    quick_sort(array, start, right-1)
    quick_sort(array, right+1, end)

quick_sort(array, 0, len(array)-1)
array

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

# ** 퀵 정렬2 - 파이썬의 장점을 살린 방식 **

array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]

def quick_sort(array):
    if len(array) <= 1:
        return array
    pivot = array[0]
    not_pivot = array[1:]
    
    left_side = [x for x in not_pivot if x <= pivot]
    right_side = [x for x in not_pivot if x > pivot]
    
    return quick_sort(left_side) + [pivot] + quick_sort(right_side)

print(quick_sort(array))

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

계수 정렬

특정한 조건이 부합할 때만 사용할 수 있지만 매우 빠르게 동작하는 알고리즘
- 계수 정렬은 데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때 사용 가능
- 계수 정렬ㅇ느 동일한 값을 가지는 데이터가 여러 개 등장할 때 효과적으로 사용할 수 있다.
시간 복잡도: 최악의 경우에도 수행시간 O(N + K)를 보장
계수 정렬은 때에 따라서 심각한 비효율성을 초래할 수 있음
- 데이터가 0과 999,999만 존재하는 경우(공간 복잡도 증가)
계수 정렬 동작 예시
1. 가장 작은 데이터부터 가장 큰 데이터까지의 범위가 모두 담길 수 있도록 리스트를 초기화(0)
2. 데이터를 하나씩 확인하며 데이터의 값과 동일한 인덱스의 데이터를 1씩 증가시킴
3. 결과를 확인할 땐 리스트의 첫 번쨰 데이터부터 하나씩 그 값만큼 반복하여 인덱스를 출력

array = [7, 5, 9, 0, 3, 1, 6, 2, 9, 1, 4, 8, 0, 5, 2]

# 모든 범위를 포함하는 리스트 선언 및 초기화
count = [0 for i in range(max(array) + 1)]
# 카운트
for i in range(len(array)):
    count[array[i]] += 1

# 출력
for i in range(len(count)):  
    for j in range(count[i]): # coubt[i]의 수만큼 반복
        print(i, end = ' ')

0 0 1 1 2 2 3 4 5 5 6 7 8 9 9

이진 탐색 알고리즘

순차 탐색: 리스트 안에 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 확인하는 방법
이진 탐색: 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 기법
- 이진 탐색은 시작점, 끝점, 중간점을 이용하여 탐색 범위를 설정함|
시간 복잡도: $O(logN)$
큰 탐색 범위를 보면 가장 먼저 이진 탐색을 떠올려야 함

def binary_search(array, target, start, end):
    if start > end:
        return False
    mid = (start + end) // 2
    
    if array[mid] == target:
        return mid    
    elif array[mid] > target:
        return binary_search(array, target, start, mid - 1)
    else:
        return binary_search(array, target, mid + 1, end)

array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
array.sort()

result = binary_search(array, 6, 0, len(array) - 1)
print(result)

파이썬 이진 탐색 라이브러리(bisect)

bisect_left(a, x): 정렬된 순서를 유지하면서 배열 a에 x를 삽입할 가장 왼쪽 인덱스를 반환
bisect_right(a, x): 정렬된 순서를 유지하면서 배열 a에 x를 삽입할 가장 오른쪽 인덱스를 반환
참고 : 값이 특정 범위에 속하는 데이터 개수 구할 때
- bisect_left결과와 bisect_left결과의 차이를 통해 할 수 있음

from bisect import bisect_left, bisect_right

a = [1, 2, 4, 4, 8]
x = 4

print(a)
print(bisect_left(a, x))  # 인덱스 반환
print(bisect_right(a, x))  # 인덱스 반환

[1, 2, 4, 4, 8]
2
4

파라메트릭 서치(Parametric Search)

파라메트릭 서치란 최적화 문제를 결정 문제(예 혹은 아니오)로 바꾸어 해결하는 기법
- ex) 특정한 조건을 만족하는 가장 알맞은 값을 빠르게 찾는 최적화문제
일반적으로 코딩 테스트에서 파라메트릭 서치 문제는 이진 탐색을 통해 해결할 수 있음.
큰 탐색 범위를 보면 가장 먼저 이진 탐색을 떠올려야 함

다이나믹 프로그래밍(동적 계획법)

다이나믹 프로그래밍은 메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상시키는 방법
- 이미 계산된 결과(작은 문제)는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 한다.
다이나믹 프로그래밍의 구현은 일반적으로 두 가지 방식(탑 다운과 바텀 업)으로 구성됨
다이나믹 프로그래밍의 조건
1. 최적 부분 구조(optimal substructure)
  - 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있다.
2. 중복되는 부분 문제(overlapping subproblem)(여러 번 등장)
  - 동일한 작은 문제를 반복적으로 해결해야 한다
시간 복잡도
- 메모이제이션을 이용하는 경우: $O(N)$

피보나치 수열

특정 k번째 피보나치 수는 앞 두 개의 피보나치 수를 더한 값임(1, 1, 2, 3, 5, 8, 13, 21, 34, ..., inf)
점화식이란 인접한 항들 사이의 관계식을 의미함
- 피보나치 수열의 점화식 : an = an-1 + an-2 |||| a1 = 1, a2 = 1

피보나치 - 단순 재귀

# 피보나치 - 단순 재귀
def fibo(x):
    if x == 1 or x == 2 : 
        return 1
    return fibo(x - 1) + fibo(x - 2)

fibo(10)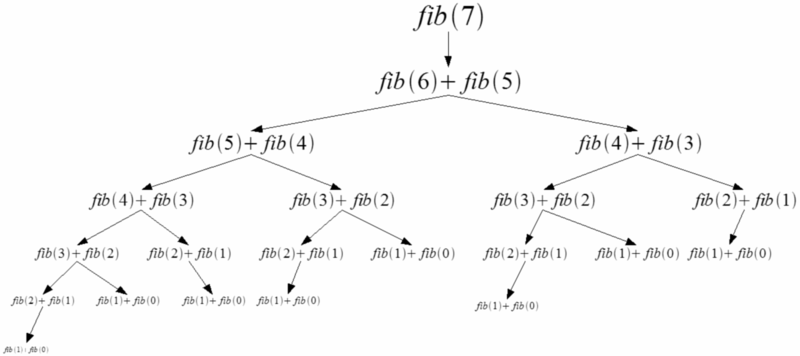

재귀함수 피보나치의 비효율성
- 위 그림을 보면, 3번째 피보나치 수를 구하는 fibo(3)가 4번 발생한 것을 볼 수 있음
- 시간 복잡도: O(2^N)
- 빅오 표기법을 기준으로 fibo(30)을 계산하기 위해선 약 10억 가량의 연산을 수행해야 함

피보나치의 효율적인 해법 : 다이나믹 프로그래밍

다이나믹 프로그래밍의 사용 조건을 만족하는지 확인
1. 최적 부분 구조: 큰 문제를 작은 문제로 나눌 수 있다.
  - fibo(4)를 구하려면 fibo(3)과 fibo(2)로 해결할 수 있음
2. 중복되는 부분문제: 동일한 작은 문제를 반복적으로 해결한다.
  - 같은 fibo(n)이 여러번 사용됨

피보나치는 다이나믹 프로그래밍의 사용 조건을 만족함

메모이제이션(하향식, 탑다운)
- 한 번 계산한 결과를 메모리 공간에 메모하는 기법
  - 같은 문제를 다시 호출하면 메모했던 결과를 그대로 가져옴
  - 값을 기록해 놓는다는 점에서 캐싱(caching)이라고도 함

탑다운(하향식) vs 바텀업(상향식)

다이나믹 프로그래밍의 전형적인 형태는 바텀업 방식임(반복문)
- (결과 저장용 리스트는 DP테이블이라고 부름)
엄밀히 말하면 메모이제이션은 이전에 계산된 결과를 일시적으로 기록해놓는 넓은 개념을 의미
- 따라서 메모이제이션은 다이나믹 프로그래밍에 국한된 개념은 아님
- 한 번 계산된 결과를 담아 놓기만 하고 다이나믹 프로그래밍을 위해 활용하지 않을 수도 있음

# 피보나치 - 탑다운 다이나믹 프로그래밍(재귀)

# 한 번 계산된 결과를 메모이제이션 하기 위한 리스트 초기화 0 ~ 99
d = [0] * 100

# 피보나치 함수를 재귀함수로 구현(탑다운 다이나믹 프로그래밍)
def fibo(x):
    if x == 1 or x == 2:
        return 1
    
    # 이미 계산한 적 있는 문제라면 그대로 반환(메모이제이션)
    if d[x] != 0:
        return d[x]
    
    # 계산하지 않은 문제는 점화식에 따라 피보나치 결과 반환
    d[x] = fibo(x - 1) + fibo(x - 2)
    return d[x]

print(fibo(99))

218922995834555169026

# 피보나치 - 바텀업 다이나믹 프로그래밍(반복문)

d = [0] * 100

# 첫 번째 피보나치 수와 두 번쨰 피보나치 수는 1
d[1], d[2] = 1, 1

n = 99
# 피보나치 함수 반복문으로 구현(바텀업 다이나믹 프로그래밍)
for i in range(3, n + 1):
    d[i] = d[i - 1] + d[i - 2]

print(d[n])

218922995834555169026

다이나믹 프로그래밍 VS 분할 정복

분할 정복
- 문제를 나눌 수 없을 때까지 나누어서 각각을 풀면서 다시 합병하여 문제의 답을 얻는 알고리즘
- 하향식 접근법으로, 상위의 해답을 구하기 위해, 아래로 내려가면서 하위의 해답을 구하는 방식
  - 일반적으로 재귀 함수로 구현
- 문제를 잘게 쪼갤 때, 부분 문제는 서로 중복되지 않음
  - ex) 병합 정렬, 퀵 정렬 등
다이나믹 프로그래밍과 분할 정복은 모두 최적 부분 구조를 가질 떄 사용할 수 있다.
- 큰 문제를 작은 무제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있는 상황
다이나믹 프로그래밍과 분할 정복의 차이점은 부분 문제의 중복이다.
- 다이나믹 프로그래밍 문제에서는 각 부분 문제제들이 서로 영향을 미치며 부분 문제가 종복된다.
- 분할 정복 문제에서는 동일한 부분 문제가 반복적으로 계산되지 않는다

다이나믹 프로그래밍 문제에 접근하는 방법

주어진 문제가 다이나믹 프로그래밍 유형임을 파악하는 것이 중요
가장 먼저 그리디, 구현, 완전 탐색 등의 아이디어로 문제를 해결할 수 있는지 검토
- 다른 알고리즘으로 풀이 방법이 떠오르지 않으면 다이나믹 프로그래밍을 고려
일단 재귀 함수로 비효율적인 완전 탐색 프로그램을 작성한 뒤에(탑다운) 작은 문제에서 구한 답이 큰 문제에서 그대로 사용될 수 있으면, 코드를 개선하는 방법을 사용
일반적인 코딩 테스트 수준에서는 기본 유형의 다이나믹 프로그래밍 문제가 출제되는 경우가 많음

백트래킹(Back-Tracking)

[백준] N과 M(기본)

# 백트래킹 사용
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
 
sup = []
 
def dfs():
    if len(sup)==m:
        print(' '.join(map(str, sup)))
        return
    
    for i in range(1,n+1):
        if i not in sup:
            sup.append(i)
            dfs()
            sup.pop()
 
dfs()

[백준] N-Queen

def check(x):
    for r in range(x):
        # 같은 열  or  대각(열-열 == 행-행)
        if row[x] == row[r] or abs(row[x] - row[r]) == abs(x - r):
            return False

    return True


def dfs(x):
    global result
    if x == n:
        result += 1
        return

    else:
        for col in range(n):  # col
            # [x, col]: queen
            row[x] = col  # [0,0] -> [1,0]
            if check(x):
                dfs(x + 1)


n = int(input())
row = [0 for _ in range(n)]
result = 0

dfs(0)
print(result)

whatSup CheatSheet

AI Engineer : Lv 0

다음 포스트

기초 알고리즘 정리

자주 사용되는 표준 라이브러리

자주 사용되는 내장함수 & 알고리즘

itertools

collectios.Counter

최대 공약수와 최소 공배수

heapq(우선순위 큐)

리스트

세트

딕셔너리

할당

얕은 복사와 깊은 복사

문자열

대/소문자 변환

문자열 탐색

문자열 구성

공백제거, 대체

쪼개기, 합치기

포맷팅

정규표현식

정규표현식에서 사용되는 메타 문자들

파이썬 re 모듈

파이썬 컴프리핸션

chr

파이썬 Nonlocal, global

time.timedelta

그리디(greedy) 알고리즘

구현(Implementation)

그래프 탐색 알고리즘: DFS/BFS

스택과 큐

스택

큐

재귀함수

DFS(깊이 우선 탐색)

BFS(너비 우선 탐색)

주의

정렬 알고리즘

선택(Selection) 정렬

삽입(Insert) 정렬

퀵(Quick) 정렬

계수 정렬

이진 탐색 알고리즘

파이썬 이진 탐색 라이브러리(bisect)

파라메트릭 서치(Parametric Search)

다이나믹 프로그래밍(동적 계획법)

피보나치 수열

피보나치 - 단순 재귀

피보나치의 효율적인 해법 : 다이나믹 프로그래밍

탑다운(하향식) vs 바텀업(상향식)

다이나믹 프로그래밍 VS 분할 정복

다이나믹 프로그래밍 문제에 접근하는 방법

백트래킹(Back-Tracking)

[백준] N과 M(기본)

[백준] N-Queen

기초 알고리즘 정리

0개의 댓글

관련 채용 정보