이진 탐색 알고리즘이란?

이진 탐색 알고리즘 (Binary Search)

• 순차 탐색의 시간복잡도가 크기 때문에 정렬되어 있는 리스트에서 탐색 범위를 좁혀가며 데이터를 탐색하는 방법이다.
• 순차 탐색의 시간 복잡도를 $log$ 만큼 줄일 수 있다.
• n이 엄청 큰 경우, 시간복잡도를 $O(log N)$으로 처리해야겠다라고 생각이 드는 경우 시도해볼법한 알고리즘이다.

N 이 1,000,000(백만) 일 때, log N = 19.93 이 된다.

이진 탐색 동작 방법

• [step 1] 시작점, 끝 점, 중간점 설정
• [step 2] 중간점의 값과 찾고자하는 값 비교
  • [step 2-1] 비교 후 중간점의 값이 내가 찾고자하는 값이라면 중간점 반환
  • [step 2-2] 비교 후 중간점의 값이 내가 찾고자하는 값보다 크다면
    • 끝 점의 인덱스를 중간점으로 이동하여 다음번 탐색 범위를 반으로 줄인다.
      (이미 정렬되어 있는 배열을 이용하므로 0번 인덱스 ~ 중간 까지의 값들은
      찾고자하는 값보다 더 작으므로 탐색할 필요가 없다.)
  • [step 2-3] 비교 후 중간점의 값이 내가 찾고자하는 값보다 작다면
    • 시작점의 인덱스를 중간점으로 이동하여 다음번 탐색 범위를 반으로 줄인다.

구현 방법

재귀함수를 이용한 구현

def binary_search(array, start, end, target):
    """
    Args 
        array   (list)  : 이진탐색을 진행할 정렬이 되어 있는 값이 저장되어있는 리스트
        start   (int)   : 탐색을 시작할 인덱스
        end     (int)   : 탐색을 끝낼 인덱스
        target  (int)   : 찾고자하는 값
    """
    if start > end:
        return None

    # 구간 설정 (이진 탐색을 진행하기 위해 첫 인덱스와 끝 인덱스를 더하여 반으로 나눔.)
    mid = (start + end) // 2
    
    # 찾은 경우 인덱스를 반환
    if array[mid] == target:
        return mid
        
    # 중간값이 target보다 작다면 중간값 + 1 부터 끝인덱스까지 재귀적으로 탐색
    elif array[mid] <= target:
        return binary_search(array, mid + 1, end, target)
        
    # 중간값이 target보다 크다면 첫 인덱스부터 중간값 - 1 까지 재귀적으로 탐색
    else:
        return binary_search(array, start, mid - 1, target)

반복문을 이용한 구현

def binary_search(array, start, end, target):
    while start <= end:
        mid = (start + end) // 2

        if array[mid] == target:
        	return mid
        elif array[mid] < target:
        	start = mid + 1
        else:
            end = mid -1
        
    return None

시간 복잡도

단계마다 탐색 범위를 2로 나누는 것과 동일하므로 $O(log N)$ 이다.

파이썬 이진 탐색 라이브러리

bisect_left(arr, x)

정렬된 순서를 유지하면서 배열 a에 x를 삽입할 가장 왼쪽 인덱스를 반환
lower bound의 개념이다.

bisect_right(arr, x)

정렬된 순서를 유지하면서 배열 a에 x를 삽입할 가장 오른쪽 인덱스를 반환
upper bound의 개념이다.

from bisect import bisect_left, bisect_right

a = [1, 2, 3, 4]
x = 4

print(bisect_left(a, x))    # 2
print(bisect_right(a, x))   # 4

bisect를 이용하여 특정 범위에 있는 데이터의 개수 구하기

from bisect import bisect_left, bisect_right

a = [1, 2, 3, 4]
x = 4

print(bisect_left(a, x))    # 2
print(bisect_right(a, x))   # 4

값이 특정 범위에 속하는 데이터 개수 구하기

from bisect import bisect_left, bisect_right

# 값이 [left_value, right_value]인 데이터의 개수를 반환하는 함수
def count_by_range(a, left_value, right_value):
    right_index = bisect_right(a, right_value)
    left_index = bisect_left(a, left_value)
    return right_index - left_index

# 배열 선언
a = [1, 2, 3, 3, 3, 3, 4, 4, 8, 9]

# 값이 4인 데이터 개수 출력
print(count_by_range(a, 4, 4))

# 값이 [2, 5] 범위에 있는 데이터 개수 출력
print(count_by_range(a, 2, 5))

lower bound와 upper bound가 필요한 이유

그림과 같이 정렬된 리스트 array에서 target이 추가된다고 할 때
어느 자리(인덱스)에 넣어야 리스트의 정렬을 유지할 수 있을까?

일반적인 binary search는 찾고자 하는 숫자를 찾아주지만
찾고자하는 숫자가 array리스트에 여러 개가 있다면
nums 배열의 길이에 따라 어떤 인덱스가 반환될지 모른다. (일관성이 없다.)

예 ) array 리스트에서 2를 찾고 싶을 때 일반적인 binary search 를 이용하면
리스트의 길이에 따라 끝 점과 중간점의 값이 변하므로,
1, 2, 3, 4 중에 반환되는 값이 달라질 수 있다.

- lower bound의 경우

• 찾고자하는 수를 만났을 때, 그 수가 찾고자 하는 수 중에서 가장 작은 인덱스가 아닐 수 있기 때문에 탐색 범위를 좁혀서 더 탐색을 진행한다.

• lower bound 파이썬 코드

def lowerbound(target, lst):
	low, high = 0, len(lst)
    while low < high:
    	mid = (low + high) // 2
        if target <= lst[mid]:
        	high = mid
        else:
        	low = mid + 1
   return low

- upper bound의 경우

• 찾고자하는 값을 만났을 경우 탐색 범위를 아래 절반이 아닌 위 절반으로 설정하여 찾고자 하는 수가 또 있는지 탐색한다.

• upper bound 파이썬 코드

def upperbound(target, lst):
	low, high = 0, len(lst)
    while low < high:
    	mid = (low + high) // 2
        if target < lst[mid]:
        	high = mid
        else:
        	low = mid + 1
   return low

lower bound와 upper bound의 코드는 거의 비슷하기 때문에 이런식으로 합쳐서 작성할 수 도 있다.

def bound_search(target, lst, compare):
	low, high = 0, len(lst)
    while low < high:
    	mid = (low + start) // 2
        if compare(x, list[mid])
        	high = mid
       	else:
        	low = mid + 1
   return low
   
lower = lambda x, elem: x <= elem
upper = lambda x, elem: x < elem

Lower Bound의 과정

다음과 같이 2를 array list에 넣으면서 정렬을 유지하려고 할 때
들어갈 수 있는 인덱스 중의 가장 작은 값을 반환하고자 할 때 사용한다.

따라서 중간점의 값이 찾고자하는 target보다 크거나 같다면
탐색 종료 인덱스를 중간점의 인덱스로 옮겨서
중간점보다 인덱스가 작으면서 target보다 크거나 같은 인덱스가 있는지 확인한다.

찾고자하는 값 : 2
원하는 결과 값(lower bound) : 인덱스 1

(1) low = 0, high = 8, mid = 4

(2) array[mid] 의 값과 찾고자하는 target 값과 비교

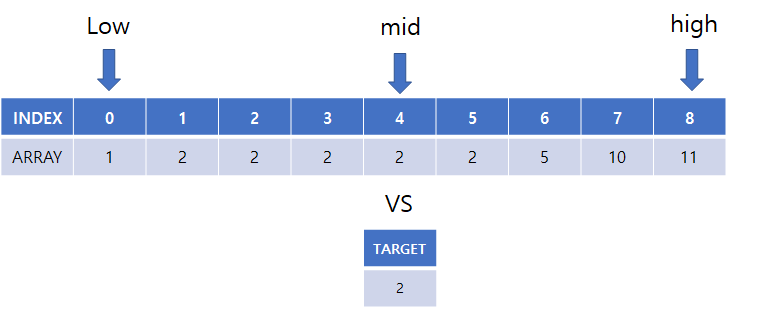
(3) high = mid 로 탐색 종료 위치 변경

(4) 다시 low = 0, high = 4, mid = 2 로 시작, 중간, 끝 점 설정 후
array[mid] 의 값과 찾고자하는 target 값과 비교

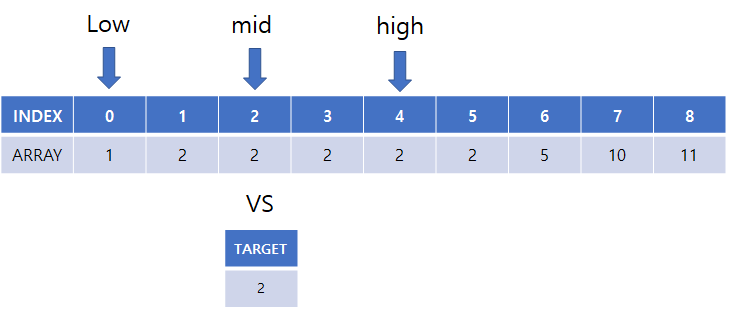
(5) high = mid 로 탐색 종료 위치 변경

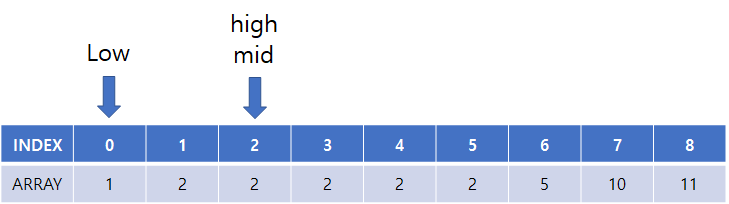
(6) 시작, 중간, 끝 점 설정 후 target과 비교

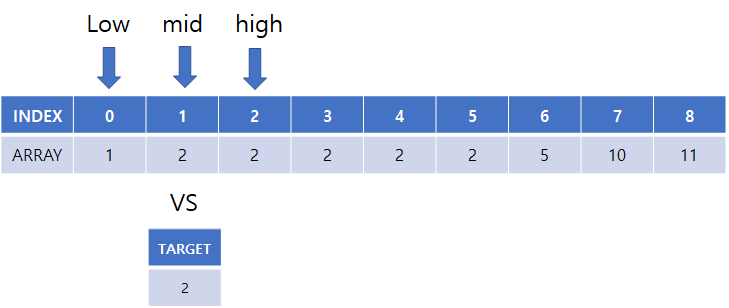
(7) high = mid 로 탐색 종료 위치 변경

(8) 시작, 중간, 끝 점 설정 후 target과 비교

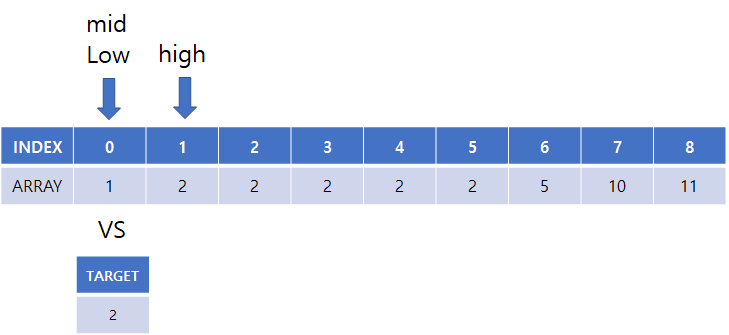
(9) low의 위치를 mid + 1로 설정

(10) 반복문 탈출하여 인덱스 반환

---

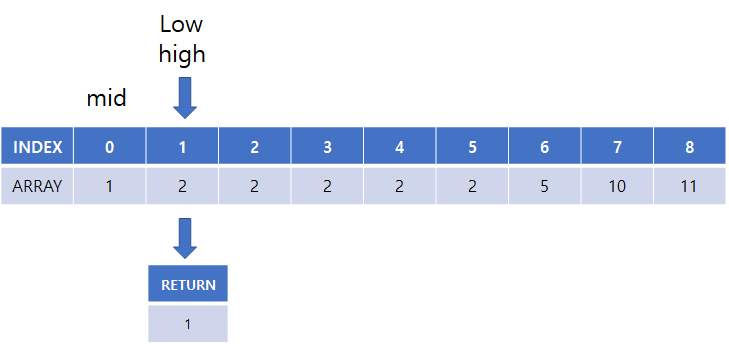
• 단순 이진 탐색의 구현은 괜찮은데, 이진 탐색을 이용하여 결과가 YES or NO로 이뤄진 결정 문제를 최적화 알고리즘으로 바꾸어 해결하는 파라메트릭 서치의 구현이 아직 서툴다.
• 이진 탐색의 경계값 설정과 결정 문제의 조건을 이용하여 이진 탐색의 범위를 좁혀가면서 탐색하는 코드를 구현하는 능력이 부족하다.
• lower bound와 upper bound의 경계값 설정이 헷갈린다.

---

참고 자료

• Lower bound & upper bound binary search (Youtube)
• 이분 탐색(Binary Search) 헷갈리지 않게 구현하기 (BOJ 블로그)

---