백준 1707 | 이분 그래프 (DFS&BFS)

문제 출처 : https://www.acmicpc.net/problem/1707

문제

그래프의 정점의 집합을 둘로 분할할 때, 모든 인접한 노드끼리의 집합이 서로 다른 그래프를 이분 그래프라고 한다.
그래프의 정점의 개수와 간선 정보가 주어질 때
이 그래프가 이분 그래프인가? 아닌가? 를 출력하는 문제이다.

입력

k : 테스트 케이스 개수 ( 1 <= k <= 5 )
v : 정점의 개수 ( 1 <= v <= 20,000 )
e : 간선의 개수 (두 정점의 번호, 1 <= e <= 200,000 )

문제 접근 방법

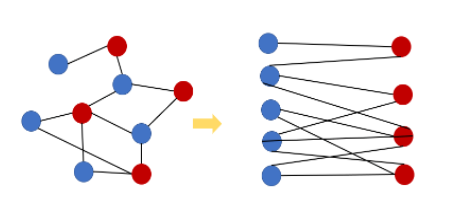
처음에는 문제에서 설명하는 이분 그래프가 뭔지 몰라서 위키 백과를 참조했다.
위 그림 처럼 집합 정보를 색으로 표현하는 것이 이해하기 더 쉬운것 같다.

BFS를 이용한 구현 과정

1. 집합 정보(코드에서는 상태 status 로 표현함)를 저장할 리스트를 선언한다
   (0 : 아직 그룹화 안함, 1 : 파랑, 2 : 빨강 )

2. 시작노드부터 BFS를 돌면서 부모노드와 자식노드의 status를 확인한다.
   1) 자식 노드의 상태가 없다면 부모 노드의 상태와 반대로 저장한다.
   status[child] = -status[parent]
   2) 자식 노드의 상태가 있는데 부모 노드와 상태가 같다면, 이분 그래프가 아니므로 False를 반환한다.

3. 모든 노드가 연결되어 있지 않을 수 있으므로 모든 노드들에 대해 아직 상태 status 가 없다면 해당 노드를 시작노드로 BFS를 진행한다.

포인트

• 집합 정보status 를 확인하기 위해서는
  다른 DFS & BFS 문제와 다르게 이미 방문 노드에 대해서도 집합 정보status 를 확인해야한다.
  ( visited 배열 필요 없음 )

• 모든 노드가 연결되어 있지 않을 수 있기 때문에
  각 노드에 대해서 상태 status 가 0 일 때, BFS를 실행하여 노드를 그룹화해야한다.

BFS 코드

import sys
from collections import deque

def bfs(x):

    # 탐색 시작 노드를 큐에 넣고 초기 상태를 1로 설정한다.
    queue = deque()
    queue.append(x)

    status[x] = 1

    while queue:
        v = queue.popleft()

        for i in graph[v]:
            # 아직 상태가 없을 경우 부모 노드와 반대로 설정한다.
            if status[i] == 0:
                status[i] = -status[v]
                queue.append(i)
            else:
                # 이전에 상태를 이미 지정해줬는데 
                # 부모노드와 자식노드의 상태가 같다면 
                # 이분 그래프가 아니므로 False를 반환한다.
                if status[i] == status[v]:
                    return False

    return True
            

k = int(sys.stdin.readline())

for _ in range(k):
    # v : 정점의 개수, e : 간선의 개수
    v, e = map(int, sys.stdin.readline().split())
    
    # graph : 인접 노드 정보, visited : 방문 정보, status : 집합 정보 
    graph = [[] for _ in range(v + 1)]
    status = [0] * (v + 1)

    # 간선의 정보 입력 받음
    for _ in range(e):
        a, b = map(int, sys.stdin.readline().split())
        graph[a].append(b)
        graph[b].append(a)

    """
    (주의) 모든 노드가 연결되어 있지 않고 떨어져 있을 때를 생각해야한다.
    (입력 예시) 
        1 (테스트 케이스 개수)
        2 (간선 개수)
        1 3 (긴선 정보, 1과 3이 연결되어 있다)
        4 5 (긴선 정보, 4와 5가 연결되어 있다)
    이렇게 떨어져 있는 그래프 일 수 있으므로 각 노드 별로 
    인접 노드중에 같은 집합이 있는지를 bfs를 통해 확인한다.
    """
    flag = True
    
    for i in range(1, v + 1):
        if status[i] == 0:
            if not bfs(i):
                flag = False
    
    if flag:
        print('YES')
    else:
        print('NO')

아예 떨어진 그래프일 수 있다는 생각을 하기 어려웠던것 같다. 문제를 더 많이 풀어보자.