백준 6549 | 히스토그램에서 가장 큰 직사각형 (분할정복)

문제 출처 : https://www.acmicpc.net/problem/6549

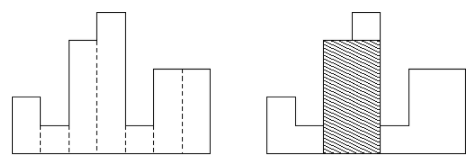
이 문제는 푸는 방법에는 여러방법이 있을 수 있지만 알아본 결과 대표적으로 3가지 방법이 있다.

풀이방법 1 : 각 직사각형의 인덱스를 이용한 분할 정복

인덱스를 기준으로 인덱스 왼쪽 구간, 가운데 구간, 인덱스 오른쪽 구간으로 분할하여 각 구간에서 나온 값의 최댓값을 리턴한다.
가운데 구간에서 어떻게 직사각형 넓이의 최댓값을 찾을 것 인지가 관건이다.

풀이방법 2 : 세그먼트 트리를 이용한 분할정복

매 구간의 높이가 가장 낮은 직사각형을 찾고 그 직사각형을 기준으로 하여 왼쪽 구간, 오른쪽 구간, 가운데 구간으로 나눠서 분할 정복을 한다.

매 구간에서 가장 높이가 낮은 직사각형을 찾는 것이 어렵지만 찾기만 하면 1번에 비해 가운데 부분의 직사각형의 넓이를 구하기 쉽다.

가운데 구간의 가장 큰 직사각형 넓이 = 높이가 제일 작은 직사각형의 높이 x 밑변의 길이 (분할하기 전의 총 밑변의 길이

세그먼트 트리를 이용하면 부분 합, 최솟값 구간의 최솟값 등을 $O(log N)$ 으로 구할 수 있다.
이 문제도 세그먼트 트리를 이용하여 $O(log n)$ 의 시간복잡도로 높이가 가장 낮은 직사각형을 찾아야 한다.
파이썬으로 세그먼트 트리를 구현하는 방법에 대해서는 더 공부할 예정이다.

풀이방법 3 : 스택을 이용한 방법

풀이방벙 2, 3은 더 공부를 해야한다.
스택을 이용한 풀이의 경우 시간복잡도가 $O(N)$ 에 가깝다고 하니 더 공부할 필요가 있을 것 같다.

문제 접근 방법

1. 기본적으로 분할정복으로 풀기 위하여 어떻게 구간을 나눌 것인지 생각한다.
2. 풀이방법 1 에서는 인덱스를 기준으로 왼쪽, 가운데, 오른쪽으로 구간을 나눴다.
3. 왼쪽, 오른쪽 구간의 경우에는 재귀적으로 가장 넓은 직사각형의 넓이가 반환되도록 divide 함수의 큰 틀을 잡아 놓는다.
4. 더 이상 나눌 수 없을 때까지 분할하였을 때 (이 문제의 경우에는 모든 직사각형이 각각 하나씩 나뉘었을 때) return 한다.
5. 가운데 구간의 직사각형 넓이의 최댓값을 구하는것이 이 문제의 핵심
6. 왼쪽 구간, 오른쪽 구간으로 나눈 경계선(인덱스를 기준으로 하는 선)을 포함하는 왼쪽 직사각형과 오른쪽 직사각형을
   중간 구간의 시작으로 설정한다.
7. 이 두 직사각형으로 최대 직사각형의 넓이를 구하면
   높이 = min(왼쪽 직사각형의 높이, 오른쪽 직사각형의 높이)
   밑변의 길이 = 2 가 되어
   현재까지 중간 구간의 직사각형의 넓이 = min(왼쪽 직사각형의 높이, 오른쪽 직사각형의 높이) * 2 가 된다.
8. 구간의 범위를 벗어나지 않게 left와 right를 각각 -1, +1 하면서 이전까지의 넓이와 비교하여 큰 값을 저장한다.
9. 왼쪽으로 한 칸 갈지 오른쪽으로 한 칸 갈지 결정할때 항상 직사각형의 높이가 큰 방향으로 이동해야한다.
   ( 높이의 경우 항상 min값을 찾기 때문에 한번 높이가 작아지면 다시 커질 수 없다.)

코드

import sys

def divide(histograms):
    if len(histograms) == 1:
        return histograms[0]

    mid = len(histograms) // 2
    left_idx, right_idx = mid - 1, mid

    mid_height = min(histograms[left_idx], histograms[right_idx])
    mid_width = 2
    mid_max = mid_height * mid_width

    left_area = histograms[:mid]
    right_area = histograms[mid:]

    while (left_idx > 0 or right_idx < len(histograms) - 1):
        current_height = 0
        
        if left_idx == 0:
            right_idx += 1
            current_height = histograms[right_idx]

        elif right_idx == len(histograms) - 1:
            left_idx -= 1
            current_height = histograms[left_idx]

        elif histograms[left_idx - 1] > histograms[right_idx + 1]:
            left_idx -= 1
            current_height = histograms[left_idx]

        else:
            right_idx += 1
            current_height = histograms[right_idx]

        mid_height = min(current_height, mid_height)
        mid_width += 1
        mid_max = max(mid_max, mid_height * mid_width)

    return max(divide(left_area), divide(right_area), mid_max)

while True:
    case = list(map(int, sys.stdin.readline().split()))
    flag = case[0]
    histograms = case[1:]

    if not flag:
        break

    print(divide(histograms))

더 공부할 내용

• 히스토그램 문제 스택을 이용한 풀이 방법
• 세그먼트 트리, 세그먼트 트리를 이용한 히스토그램 분할 정복 풀이 방법