DINO의 학습 목표

Self-distillation with no labels 방식, 즉 DINO(DIstillation with NO labels) 프레임워크의 핵심 학습 목표는 레이블 없이 이미지 데이터 그 자체로부터 유용하고 일반화 가능한 시각적 특징(visual features)을 학습하는 것입니다. 이를 달성하기 위해 DINO는 다음과 같은 방식으로 학습이 진행됩니다.

1. 입력 이미지의 다른 "뷰" 생성: 하나의 원본 이미지로부터 다양한 랜덤 변환(augmentation)을 적용하여 여러 개의 다른 모습(view)의 이미지를 만듭니다. 논문에서는 주로 두 개의 글로벌 뷰(large resolution)와 여러 개의 로컬 뷰(small resolution)를 사용합니다.

2. 학생 네트워크와 교사 네트워크: 동일한 구조를 가진 두 개의 네트워크, 학생 네트워크와 교사 네트워크를 사용합니다. 학생 네트워크는 그래디언트 역전파를 통해 직접적으로 학습되고, 교사 네트워크는 학생 네트워크의 가중치를 EMA(지수 이동 평균) 방식으로 천천히 따라가며 업데이트됩니다. 교사 네트워크의 출력에는 추가적으로 중심화(centering) 및 날카롭게 하기(sharpening)가 적용됩니다.

3. 교사 출력을 모방하도록 학생 학습: 학생 네트워크는 변환된 뷰들(예: 로컬 뷰)을 입력받아 나온 자신의 출력 분포가, 교사 네트워크가 다른 뷰(예: 글로벌 뷰)를 입력받아 나온 출력 분포와 최대한 유사해지도록 학습됩니다. 이때 교사 네트워크의 출력에는 Stop-gradient가 적용되어 교사 네트워크 자체는 이 손실로부터 직접적인 그래디언트를 받지 않습니다.

4. 모델 붕괴 방지: 이러한 설정에서 모델이 모든 이미지에 대해 항상 동일한 출력을 내거나, 특정 차원에만 출력이 몰리는 등의 붕괴(collapse)가 발생할 수 있습니다. DINO는 교사 출력에 적용하는 중심화(Centering)와 날카롭게 하기(Sharpening), 그리고 EMA 방식으로 업데이트되는 교사 네트워크를 통해 이를 효과적으로 방지합니다.

이 과정을 통해 DINO 모델은 다음과 같은 특징을 가진 시각적 표현(representation)을 학습하게 됩니다.

• 변환 불변성 학습: 동일한 이미지의 다른 변환된 뷰에 대해 유사한 특징 표현을 생성하도록 학습됩니다. 즉, 이미지의 표면적인 변화(크기, 자르기, 색상 등)에 관계없이 핵심적인 시각적 내용을 파악하는 특징을 학습합니다.

• 의미론적/구조적 정보 포착: 다양한 뷰 간의 일관성을 맞추는 과정에서 이미지 내의 객체, 배경, 그 경계 등 의미론적이고 구조적인 정보를 특징에 담게 됩니다. 논문에서 자기 지도 학습된 ViT의 특징이 객체 분할과 같은 정보를 명시적으로 포함한다는 것이 이를 보여줍니다.

• 고품질 특징 학습: 레이블 정보 없이도 지도 학습에 버금가거나 특정 측면에서는 능가하는 고품질의 특징을 학습하여, 이미지 분류, 검색, 분할 등 다양한 다운스트림 비전 태스크에서 효과적으로 활용될 수 있습니다.

DINO framework

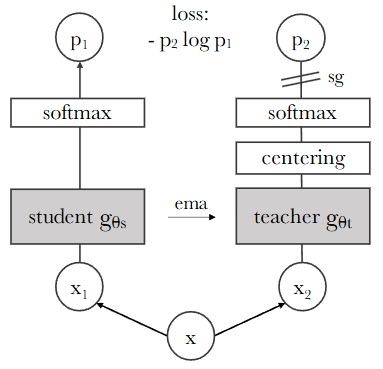
주어진 이미지는 DINO(self-distillation with no labels)라고 불리는 자기 지도 학습(self-supervised learning) 프레임워크의 구조를 보여줍니다. 이 프레임워크는 레이블 없이 학생 네트워크(student network)가 교사 네트워크(teacher network)의 출력을 모방하도록 학습시키는 방식으로 작동합니다.

주요 구성 요소는 다음과 같습니다.

• 원본 이미지 (x): 학습의 시작점인 원본 이미지입니다.

• 랜덤 변환된 뷰 (x1, x2): 원본 이미지 x로부터 두 개의 다른 랜덤 변환(augmentation)을 적용하여 얻은 이미지입니다. 논문에서는 멀티 크롭(multi-crop) 전략을 사용하여 다양한 해상도의 뷰를 생성합니다.

• 학생 네트워크 (student gθs): 학습 가능한 파라미터 θs를 가진 네트워크입니다. 변환된 뷰 x1, x2를 입력받아 출력 s1, s2를 생성합니다.

• 교사 네트워크 (teacher gθt): 파라미터 θt를 가진 네트워크입니다. 학생 네트워크와 동일한 구조를 가지지만, 파라미터는 학생 네트워크의 파라미터를 지수 이동 평균(EMA)하여 업데이트됩니다. 이 네트워크는 일반적으로 더 안정적이고 성능이 좋은 "가상" 교사 역할을 합니다. 논문에서는 일반적으로 글로벌 뷰(예: x1, x2)만 교사 네트워크에 입력으로 사용합니다.

• Centering: 교사 네트워크의 출력에 적용되는 작업으로, 배치(batch)에 대한 평균을 계산하여 출력을 중심화합니다. 이는 모델이 모든 차원에 대해 고르게 예측하도록 유도하여 붕괴(collapse)를 방지하는 데 도움을 줍니다.

• Softmax: 각 네트워크의 출력을 확률 분포 p1 (학생) 및 p2 (교사)로 변환하는 함수입니다. 이때 온도(temperature) 파라미터(τs, τt)를 사용하여 분포의 날카로움(sharpness)을 조절합니다. 교사 네트워크의 출력에는 중심화(centering) 및 날카롭게 하기(sharpening)가 적용된 후 Softmax가 계산됩니다.

• Stop-gradient (sg): 교사 네트워크의 출력 p2에 적용됩니다. 이는 손실 함수로부터 계산된 그래디언트가 교사 네트워크 gθt를 통해 역전파되는 것을 막아, 학생 네트워크 gθs만 직접적으로 업데이트되도록 합니다.

• EMA (Exponential Moving Average): 교사 네트워크의 파라미터 θt는 학생 네트워크의 파라미터 θs의 지수 이동 평균으로 업데이트됩니다. 이는 교사 네트워크가 학생 네트워크의 최근 학습 상태를 부드럽게 따라가도록 하며, 학습의 안정성과 성능 향상에 기여합니다. 업데이트 규칙은 다음과 같습니다: $\theta_t \leftarrow \lambda \theta_t + (1-\lambda)\theta_s$, 여기서 $\lambda$는 모멘텀 비율입니다.

• 손실 함수 (loss: - p2 log p1): 교사 네트워크의 출력 분포 p2와 학생 네트워크의 출력 분포 p1 사이의 유사도를 측정하는 데 사용됩니다. 이 형식은 교차 엔트로피(cross-entropy) 손실을 나타냅니다.

DINO 프레임워크는 변환된 두 뷰(x1, x2)를 각각 학생 네트워크와 교사 네트워크에 통과시킨 후, 교사 네트워크의 출력(p2)을 정답 삼아 학생 네트워크가 이를 예측하도록 학습합니다. stop-gradient 덕분에 학생 네트워크만 그래디언트를 통해 학습되고, 교사 네트워크는 학생 네트워크의 가중치 평균으로 업데이트됩니다. 이는 학생 네트워크가 스스로 생성한 "교사"의 지식을 증류(distillation)하는 과정으로 해석될 수 있으며, 명시적인 레이블 없이 효과적인 특징 학습을 가능하게 합니다. 이미지에서는 하나의 뷰(x1)를 학생과 교사에, 다른 뷰(x2)를 학생과 교사에 각각 입력으로 사용하여 손실을 계산하고 평균합니다. 그림에서는 간략하게 x1을 학생, x2를 교사에 입력하고 손실을 계산하는 경우를 보여줍니다.

손실 함수는 다음과 같이 교차 엔트로피 형태로 표현됩니다.

$H(P_t(x), P_s(x')) = - \sum_{k=1}^K P_t(x)(k) \log P_s(x')(k)$

여기서,

• $H$는 교차 엔트로피를 나타냅니다.
• $P_t(x)(k)$는 교사 네트워크가 입력 $x$에 대해 $k$번째 차원에 대해 예측한 확률입니다.
• $P_s(x')(k)$는 학생 네트워크가 입력 $x'$에 대해 $k$번째 차원에 대해 예측한 확률입니다.
• $K$는 출력 차원의 크기입니다.
• $\log$는 자연로그입니다.

이 손실 함수는 교사 네트워크가 예측한 확률 분포 $P_t(x)$를 학생 네트워크가 예측한 확률 분포 $P_s(x')$가 얼마나 잘 모방하는지를 측정합니다. 손실을 최소화함으로써 학생 네트워크는 교사 네트워크와 유사한 출력을 생성하도록 학습됩니다.

DINO와 Vision Transformer(ViT)를 함께 사용했을 때, 자기 지도 학습된 ViT 특징이 이미지의 의미론적 분할(semantic segmentation) 정보를 명시적으로 포함하고, k-NN 분류기에서 우수한 성능을 보인다는 점이 논문의 주요 발견 중 하나입니다. 이러한 특성은 지도 학습된 ViT나 컨볼루션 신경망(convnets)에서는 명확하게 나타나지 않았습니다. 또한, DINO는 모멘텀 인코더, 멀티 크롭 학습, 작은 패치 크기의 중요성을 강조하며, 이러한 요소들을 결합하여 레이블 없는 자기 증류(self-distillation) 방식으로 해석될 수 있는 DINO 프레임워크를 설계했습니다.

연구의 진전과 관련하여, Bootstrap Your Own Latent: A New Approach to Self-Supervised Learning(BYOL)과 같은 이전 자기 지도 학습 연구들은 모멘텀 인코더를 사용하여 특징을 매칭하는 방식이나, Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results(Mean Teacher)와 같은 자기 학습(self-training) 방법을 사용했습니다. DINO는 BYOL의 아이디어를 계승하지만, 다른 유사도 매칭 손실을 사용하고 학생 및 교사 네트워크에 동일한 구조를 사용하여 레이블 없는 Mean Teacher 자기 증류의 한 형태로 해석될 수 있음을 보여줍니다. 또한, Unsupervised Learning of Visual Features by Contrasting Cluster Assignments(SwAV)에서 사용된 멀티 크롭 전략과 Momentum Contrast for Unsupervised Visual Representation Learning(MoCo)에서 사용된 모멘텀 인코더가 DINO와 ViT의 조합에서 특히 중요한 구성 요소임을 실험적으로 증명했습니다. DINO는 이러한 기존 방법론의 핵심 아이디어를 효과적으로 결합하고 단순화하여 ViT의 잠재력을 자기 지도 학습 환경에서 끌어냈다는 점에서 차별점을 가집니다.

더 깊이 생각해 볼 만한 질문은 다음과 같습니다.

1. 지수 이동 평균(EMA)으로 교사 네트워크 학습 방식

• 개념: EMA는 시계열 데이터에서 최근 값에 더 큰 가중치를 주어 평균을 계산하는 방법입니다. DINO에서는 이 방법을 사용하여 교사 네트워크의 가중치를 학생 네트워크의 가중치로부터 업데이트합니다. 직접적으로 그래디언트 역전파를 통해 학습되는 학생 네트워크와 달리, 교사 네트워크는 학생 네트워크의 가중치 변화를 천천히, 그리고 부드럽게 따라가도록 설계되었습니다.

• 어떻게 작동하나요?

  • 매 학습 스텝마다 학생 네트워크는 이미지 데이터를 통해 학습되어 가중치가 업데이트됩니다.
  • 그런 다음, 교사 네트워크의 새로운 가중치($\theta_t^{\text{new}}$)는 현재 교사 네트워크의 가중치($\theta_t^{\text{old}}$)와 업데이트된 학생 네트워크의 가중치($\theta_s^{\text{new}}$)의 가중 평균으로 계산됩니다.
  • 수식으로는 다음과 같습니다: $\theta_t^{\text{new}} = \lambda \cdot \theta_t^{\text{old}} + (1 - \lambda) \cdot \theta_s^{\text{new}}$
    • 여기서 $\lambda$는 '모멘텀' 하이퍼파라미터이며, 일반적으로 1에 매우 가까운 값(예: 0.996, 0.999 등)을 사용합니다.
  • $\lambda$ 값이 크다는 것은 교사 네트워크가 이전 자신의 가중치에 더 큰 비중을 두고 학생 네트워크의 최신 변화는 적게 반영한다는 의미입니다. 이는 교사 네트워크가 학생 네트워크보다 변화에 덜 민감하고, 더 안정적인 특징을 학습하도록 만듭니다.

• 왜 사용하나요? 논문에서는 EMA를 통해 교사 네트워크가 학습 과정 전반에 걸쳐 학생 네트워크보다 더 나은 성능을 지속적으로 보인다고 언급합니다. 이렇게 "더 나은" 교사가 학생을 가이드함으로써 학생 네트워크의 학습 성능도 향상된다는 것입니다. 이는 Mean Teacher 학습 방식이나 Polyak-Ruppert averaging과 유사하게 모델 앙상블(model ensembling) 효과를 내어 더 견고한 특징을 만드는데 도움을 줍니다. 또한, 교사 네트워크로의 그래디언트 전파를 막는 Stop-gradient와 함께 사용될 때 모델 붕괴를 방지하는 핵심 요소가 됩니다.

2. 배치(batch)에 대한 평균을 계산하여 출력을 중심화(Centering)

• 개념: Centering은 교사 네트워크의 최종 출력(Softmax를 적용하기 전의 값)에서 현재 학습 배치에 포함된 모든 이미지에 대한 교사 네트워크 출력의 평균 벡터를 빼주는 작업입니다. 이는 교사 네트워크의 출력이 특정 몇 개의 차원에만 집중되는 현상(즉, 모델 붕괴의 한 형태)을 방지하는 데 도움을 줍니다.

• 예시:

  • 현재 배치에 2개의 이미지($x_1, x_2$)가 있고, 교사 네트워크의 출력이 3차원 벡터라고 가정해 봅시다.

  • 교사 네트워크가 $x_1$에 대해 출력한 원시 값(logit)이 $[1.0, 2.0, 3.0]$이고, $x_2$에 대해 출력한 원시 값이 $[0.5, 2.5, 3.5]$라고 합시다.

  • 이 배치에 대한 평균 출력 벡터는 각 차원별 평균: $[(1.0+0.5)/2, (2.0+2.5)/2, (3.0+3.5)/2] = [0.75, 2.25, 3.25]$ 입니다. 이 벡터가 Centering을 위한 '센터' 벡터($C$)가 됩니다. 실제 DINO에서는 이 센터 벡터도 EMA 방식으로 업데이트합니다 (Eq 4).

  • 이제 $x_1$에 대한 교사 출력에 Centering을 적용하면: $[1.0, 2.0, 3.0] - [0.75, 2.25, 3.25] = [0.25, -0.25, -0.25]$ 가 됩니다.

  • 마찬가지로 $x_2$에 대한 교사 출력에 Centering을 적용하면: $[0.5, 2.5, 3.5] - [0.75, 2.25, 3.25] = [-0.25, 0.25, 0.25]$ 가 됩니다.

  • Centering 후에는 각 차원 값의 절대적인 크기보다는 해당 차원 값이 배치 평균에서 얼마나 떨어져 있는지가 중요해집니다. 이는 출력이 특정 몇 개의 차원으로 쏠리는 것을 완화하고, 출력이 더 균일하게 분포되도록 만듭니다.

• Centering의 역할: 논문에서는 Centering이 출력이 한 차원에 지배되는 것을 막지만, 역으로 출력이 균일 분포(uniform distribution)로 붕괴되는 것을 유도할 수 있다고 설명합니다. 따라서 다음에 설명할 Sharpening과 함께 사용되어야 붕괴를 효과적으로 방지할 수 있습니다.

3. 온도(temperature) 파라미터(τs, τt)를 사용하여 분포의 날카로움(sharpening) 조절

• 개념: Softmax 함수는 입력 벡터의 각 요소를 확률(총합이 1인 양수)로 변환합니다. 이때 입력 벡터를 온도로 나누어주면 결과 확률 분포의 형태가 달라집니다. 온도가 낮을수록 확률 분포가 날카로워지고(가장 큰 값에 확률이 집중됨), 온도가 높을수록 분포가 부드러워져(값들이 더 고르게 분포됨) 균일 분포에 가까워집니다.

• Softmax 수식 (온도 포함): $P(i) = \frac{\exp(z_i / \tau)}{\sum_k \exp(z_k / \tau)}$

  • $z_i$는 입력 벡터의 $i$번째 값입니다.

  • $\tau$는 온도 파라미터입니다 ($\tau > 0$).

• 예시:

  • Softmax를 적용하기 전의 원시 출력 값이 $[z_1, z_2, z_3] = [1.0, 2.0, 3.0]$ 인 경우를 생각해 봅시다.

  • 온도 $\tau=1$ (기본 Softmax):
    $P(1) = \frac{\exp(1.0/1)}{\exp(1.0/1) + \exp(2.0/1) + \exp(3.0/1)} \approx \frac{2.72}{2.72 + 7.39 + 20.09} \approx 0.09$

    $P(2) = \frac{\exp(2.0/1)}{\exp(1.0/1) + \exp(2.0/1) + \exp(3.0/1)} \approx \frac{7.39}{2.72 + 7.39 + 20.09} \approx 0.24$

    $P(3) = \frac{\exp(3.0/1)}{\exp(1.0/1) + \exp(2.0/1) + \exp(3.0/1)} \approx \frac{20.09}{2.72 + 7.39 + 20.09} \approx 0.67$
    결과 확률 분포: $[0.09, 0.24, 0.67]$

  • 온도 $\tau=0.1$ (낮은 온도, Sharpening):
    $P(1) = \frac{\exp(1.0/0.1)}{\exp(1.0/0.1) + \exp(2.0/0.1) + \exp(3.0/0.1)} = \frac{\exp(10)}{\exp(10) + \exp(20) + \exp(30)} \approx 0$

    $P(2) = \frac{\exp(2.0/0.1)}{\exp(1.0/0.1) + \exp(2.0/0.1) + \exp(3.0/0.1)} = \frac{\exp(20)}{\exp(10) + \exp(20) + \exp(30)} \approx 0$

    $P(3) = \frac{\exp(3.0/0.1)}{\exp(1.0/0.1) + \exp(2.0/0.1) + \exp(3.0/0.1)} = \frac{\exp(30)}{\exp(10) + \exp(20) + \exp(30)} \approx 1$

    결과 확률 분포: $[ \approx 0, \approx 0, \approx 1]$. 가장 큰 값(3.0)에 확률이 매우 집중되어 분포가 날카로워졌습니다.

  • 온도 $\tau=10$ (높은 온도, Smoothing):
    $P(1) = \frac{\exp(1.0/10)}{\exp(1.0/10) + \exp(2.0/10) + \exp(3.0/10)} = \frac{\exp(0.1)}{\exp(0.1) + \exp(0.2) + \exp(0.3)} \approx \frac{1.11}{1.11 + 1.22 + 1.35} \approx 0.29$

    $P(2) = \frac{\exp(2.0/10)}{\exp(1.0/10) + \exp(2.0/10) + \exp(3.0/10)} = \frac{\exp(0.2)}{\exp(0.1) + \exp(0.2) + \exp(0.3)} \approx \frac{1.22}{1.11 + 1.22 + 1.35} \approx 0.32$

    $P(3) = \frac{\exp(3.0/10)}{\exp(1.0/10) + \exp(2.0/10) + \exp(0.3/10)} \approx \frac{1.35}{1.11 + 1.22 + 1.35} \approx 0.36$

    결과 확률 분포: $[0.29, 0.32, 0.36]$. 값들이 비교적 고르게 분포되어 분포가 부드러워졌습니다. 균일 분포 $[1/3, 1/3, 1/3] \approx [0.33, 0.33, 0.33]$에 더 가까워졌습니다.

• DINO에서의 역할: DINO에서는 학생 네트워크의 Softmax에는 $\tau_s$ (예: 0.1)를, 교사 네트워크의 Softmax에는 $\tau_t$ (예: 0.04에서 0.07로 선형 증가)를 사용합니다. 교사 네트워크에 낮은 온도 $\tau_t$를 사용하여 출력을 날카롭게 만드는 것은 Centering이 출력을 균일하게 만들려는 경향을 상쇄하여 모델 붕괴를 막는 데 필수적입니다.

4. 교차 엔트로피(Cross-Entropy) 함수 수식 예시

• 개념: 교차 엔트로피($H$)는 정보 이론에서 두 확률 분포 간의 차이를 측정하는 방법입니다. 머신러닝에서는 주로 분류 문제에서 모델이 예측한 확률 분포가 실제 정답 확률 분포와 얼마나 일치하는지를 나타내는 손실 함수로 사용됩니다.

• 수식: $H(p, q) = - \sum_i p_i \log q_i$

  • $p$는 실제 정답 확률 분포(target distribution)입니다. 각 $p_i$는 $i$번째 클래스에 대한 실제 확률입니다.
  • $q$는 모델이 예측한 확률 분포(predicted distribution)입니다. 각 $q_i$는 $i$번째 클래스에 대한 모델의 예측 확률입니다.
  • $\log$는 자연로그입니다.

• DINO에서의 적용: DINO에서 교차 엔트로피는 교사 네트워크의 출력 확률 분포($P_t$)를 정답 삼아, 학생 네트워크의 출력 확률 분포($P_s$)가 이를 얼마나 잘 모방하는지를 측정하는 데 사용됩니다. 손실 함수는 $H(P_t, P_s)$입니다.

• 예시:

  • 교사 네트워크의 출력 확률 분포 (정답 분포 $p$): $p = [0.1, 0.2, 0.7]$ (총합은 1입니다.)

  • 학생 네트워크의 첫 번째 예측 확률 분포 ($q_1$): $q_1 = [0.05, 0.15, 0.8]$ (교사 출력과 비교적 유사)

  • 학생 네트워크의 두 번째 예측 확률 분포 ($q_2$): $q_2 = [0.5, 0.3, 0.2]$ (교사 출력과 비교적 다름)

  • $p$와 $q_1$ 사이의 교차 엔트로피 계산:

    $H(p, q_1) = - [ p_1 \log q_{1,1} + p_2 \log q_{1,2} + p_3 \log q_{1,3} ]$

    $H(p, q_1) = - [ 0.1 \log(0.05) + 0.2 \log(0.15) + 0.7 \log(0.8) ]$

    $H(p, q_1) \approx - [ 0.1 \cdot (-2.996) + 0.2 \cdot (-1.897) + 0.7 \cdot (-0.223) ]$

    $H(p, q_1) \approx - [ -0.2996 - 0.3794 - 0.1561 ] = - [-0.8351] = 0.8351$

  • $p$와 $q_2$ 사이의 교차 엔트로피 계산:

    $H(p, q_2) = - [ p_1 \log q_{2,1} + p_2 \log q_{2,2} + p_3 \log q_{2,3} ]$

    $H(p, q_2) = - [ 0.1 \log(0.5) + 0.2 \log(0.3) + 0.7 \log(0.2) ]$

    $H(p, q_2) \approx - [ 0.1 \cdot (-0.693) + 0.2 \cdot (-1.204) + 0.7 \cdot (-1.609) ]$

    $H(p, q_2) \approx - [ -0.0693 - 0.2408 - 1.1263 ] = - [-1.4364] = 1.4364$

  • 결론: 첫 번째 예측 ($q_1$)은 교사 출력($p$)과 더 유사했기 때문에 교차 엔트로피 값이 0.8351로 더 낮게 나왔습니다. 두 번째 예측 ($q_2$)은 더 달랐기 때문에 교차 엔트로피 값이 1.4364로 더 높게 나왔습니다. 학습 과정에서는 이 교차 엔트로피 손실을 최소화하여 학생 네트워크의 예측($q$)이 교사 네트워크의 출력($p$)과 최대한 유사해지도록 가중치를 업데이트합니다.