[백준] 10164번: 격자상의 경로 (tbc)

https://www.acmicpc.net/problem/10164

initial

I am really not sure why the first example given in the q the answer is 9. I can only find 3 valid ways

also my initial code is wrong for edge case like 1 1 1, where the correct ans is 1 but mine gives 0. Other test cases I think some are correct

initial backtracking code with dfs

n,m,z = map(int,input().split())
graph = [[0 for _ in range(m+1)] for _ in range(n+1)]
count=1
for i in range(1,n+1):
    for j in range(1,m+1):
        graph[i][j]=count
        count+=1
flag = False
row = z//m +1
col = z%m
if z==0:
    flag=True
ans = 0
dx = [1,0]
dy = [0,1]
visited= [[False for _ in range(m+1)] for _ in range(n+1)]

def dfs(x,y):
    global ans
    global flag
    if x==n and y==m and flag==True:
        ans+=1
        return
    for i in range(2):
        next_x = dx[i]+x
        next_y = dy[i]+y
        if 1<=next_x<=n and 1<=next_y<=m:
            if not visited[next_x][next_y]:
                if graph[next_x][next_y]==z:
                    flag = True
                visited[next_x][next_y]=True
                dfs(next_x,next_y)
                visited[next_x][next_y]=False
                if flag:
                    flag = False
                if z==0:
                    flag=True


visited[1][1]=False
dfs(1,1)
print(ans)

solution

There is a math way to calculate all the valid paths.

https://hongcoding.tistory.com/116

If there is no grid that we have to pass through, the formula is just (n+m)!//(n!*m!). But lets fuck that formula and think in terms of dp and coming from either left or up. We have done those kind of dp questions. The total possibility of paths arriving at that grid is dp[i-1][j] + dp[i][j-1].

But if there is a grid that we have to pass through, we first calculate the total valid paths to that grid that we need to pass through. Then, we calculate the total valid paths from that grid to the end grid. Finally we multiply those 2 values together. (look at that image down)

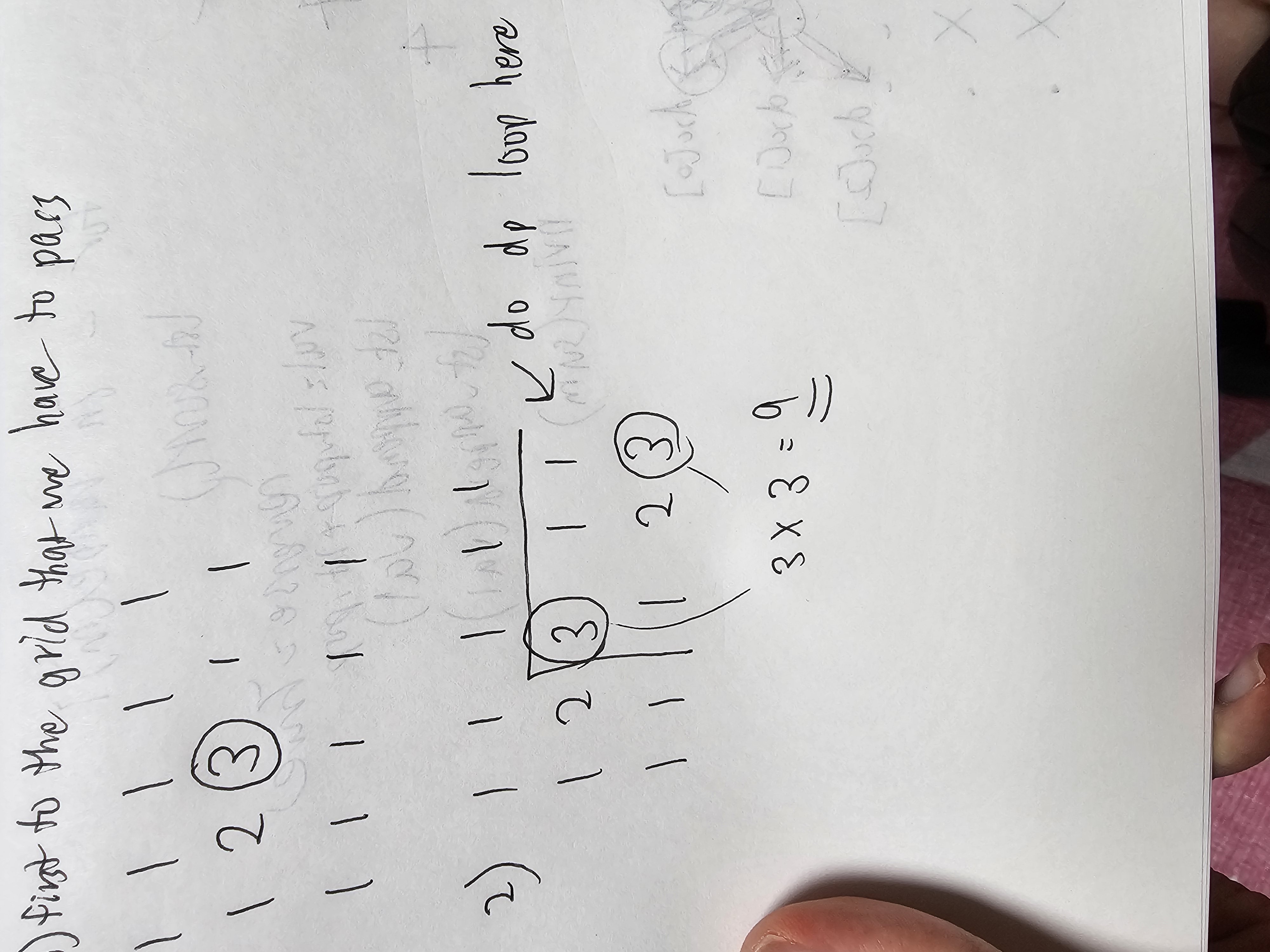
n,m,z = map(int,input().split())
dp=[[0 for _ in range(m)] for _ in range(n)]
if z==0:
    for i in range(n):
        for j in range(m):
            if i==0 or j==0:
                dp[i][j]=1
            else:
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
    print(dp[n-1][m-1])
else:
    x,y = (z-1)//m , (z-1)%m
    for i in range(x+1):
        for j in range(y+1):
            if i==0 or j==0:
                dp[i][j]=1
            else:
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
    for i in range(x,n):
        for j in range(y,m):
            if i==x and j==y:
                continue
            if i==x:
                dp[i][j]=1
            elif j==y:
                dp[i][j]=1
            else:
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
    print(dp[x][y] * dp[n-1][m-1])

complexity

The time complexity of this code is determined by the two loops that fill the dp array.

In the first loop (when z is zero), you have two nested loops over n and m, so the time complexity is O(n * m).

In the second loop (when z is not zero), you have two separate loops: one for the subrectangle defined by (x, y) and another for the remaining part. The first loop (up to (x, y)) is O(x y), and the second loop (from (x, y) to (n, m)) is O((n-x) (m-y)).

Therefore, the overall time complexity is O(n m) in the case when z is zero, and O(x y + (n-x) * (m-y)) when z is not zero.

The space complexity is O(n * m) because you create a 2D dp array of size n x m.