1.1.1 points & lines

Homogeneous representation of lines

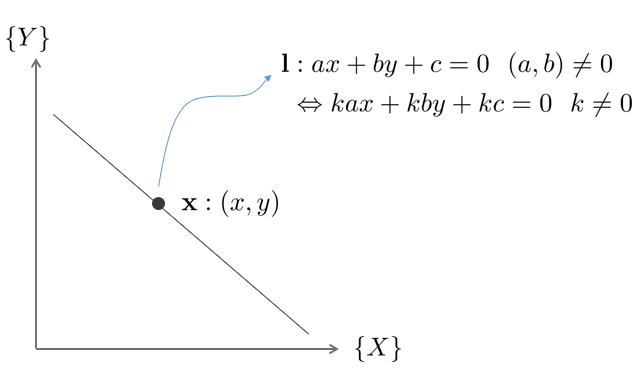
• 평면에 놓여있는 직선을 ax+by+c=0으로 표현가능하며, (a,b,c)값에 따라서 직선이 달리 표현된다.

• 직선의 벡터 (a,b,c)는 scale이 달라진다 해도 동일한 직선을 나타낸다.

• point X=(x,y)가 line $l: ax+by+c=0$에 놓여있다고 가정. 이를 수식적으로 내적을 이용하여 표현할 수 있다. $(x,y,1)(a,b,c)^T=(x,y,1)l=0$

• k(scale)에 대해서 $(kx,ky,k)l=0$을 만족하며 point를 homogenous 좌표로 나타내면 다음과 같다.

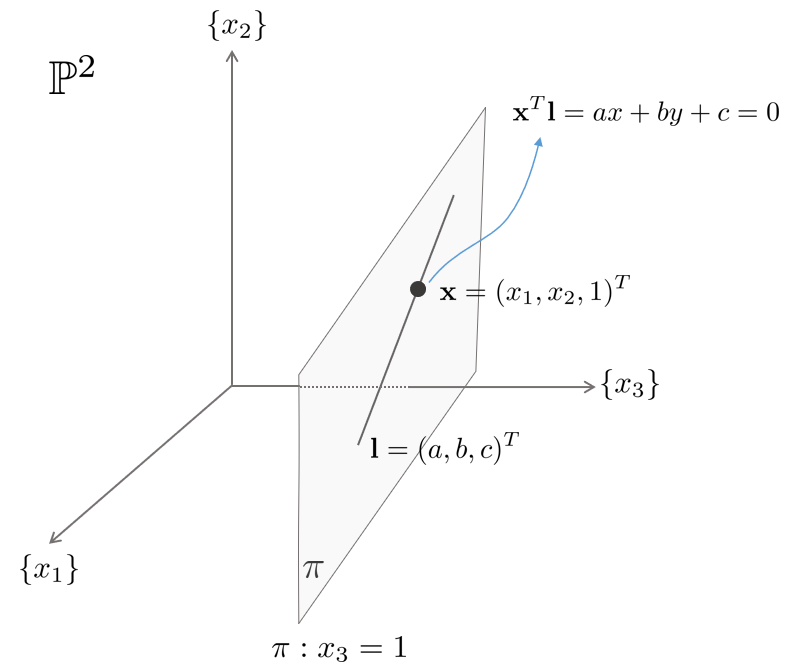
• homogeneous: $X=(x1, x2, x3)^T$ -> $\mathbb{R}^2$에 정의된 (x1/x3, x2/x3) point를 나타낸다

point X가 line $l$을 지나면, $x^Tl=0$을 만족한다

Intersection of lines

• 2개의 line $l=(a,b,c)^T$, $l'=(a',b',c')^T$가 있을 때, 두 직선의 외적의 결과인 vector x와 $l,l'$의 내적값은 수직하므로 0이 된다. $l^Tx=l'^Tx=0$

• 만약 x가 점을 나타낸다고 생각하면, $x$는 두 line의 교점이 된다.

• Ex) 두개의 line이 각각 $x=1, y=1$이라 하면, 이는 각각 $l=(-1,0,1)^T, l'=(0,-1,1)^T$로 나타난다. 교점 X는 두 벡터의 외적으로 나타남
  

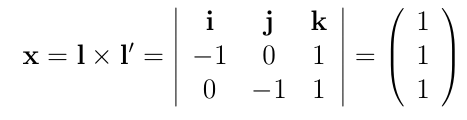
두 직선 $l,l'$의 교점은 x = l x l'으로 나타난다

Line joining points

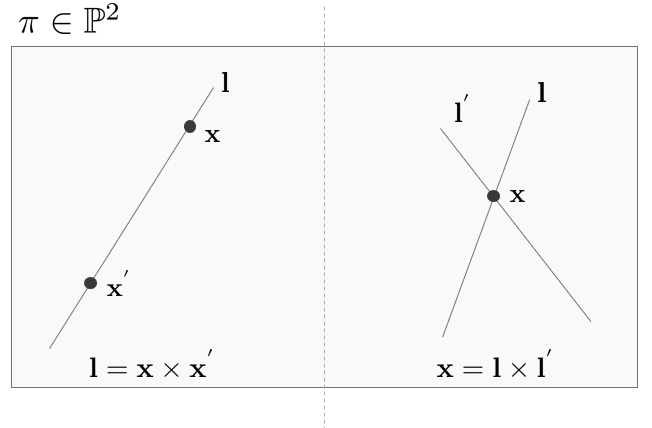
• 두개의 점 x와 x'을 지나는 직선 l은 위의 설명과 동일하게 유도될 수 있다

두 점 x와 x'을 지나는 직선은 $l=x Xx'$으로 나타난다

1.1.2 Ideal points and the line at infinity

Intersection of parallel lines

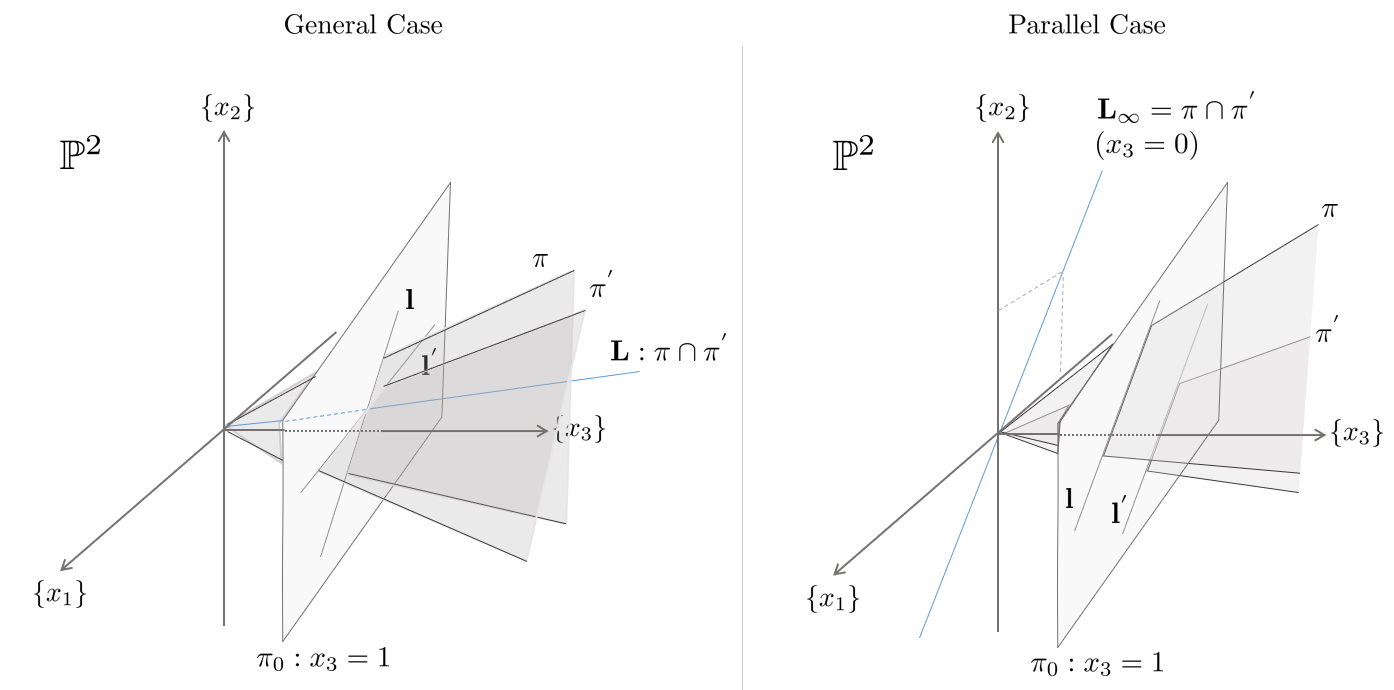
• 평행한 직선은 무한대에서 만난다. 이를 Homogenous 좌표계로 표현하면 $(x,y,0)^T$이다.

• Ex) 두개의 평행한 line $x=1, x=2$가 "무한대"에서 만난다고 가정. 교점 x는 l,l'의 외적값과 같고, 이는 실제로 y축 무한대에서 만난다.

Ideal points and the line at infinity

• Homogenous vectors $x=(x1, x2, x3)^T$ (x3는 0이 아닐때) 는 $\mathbb{R}^2$ 점에 해당된다
• 하지만 x3=0이면 $\mathbb{R}^2$에 대응되지 않고, 사영공간인 $\mathbb{P}^2$에 대응된다. 이는 ideal point라고도 불리며, 무한대 점을 의미한다
• 실제로 ideal points의 집합은 $(x1, x2, 0)^T$로 나타낼 수 있으며, 이 무한대의 점은 무한대의 선($l_{infinity}=(0,0,1)^T)$에 놓여저 있다
• 두 직선 $l=(a,b,c)^T와 l'_{infinity}=(a,b,c')$는 무한대 점 $x=(b,-a,0)^T$에서 교차한다

$\mathbb{R}^2$에서 평행한 두 직선은 $\mathbb{P}^2$공간에서 반드시 한 점에서 교차한다.

A model for the projective plane

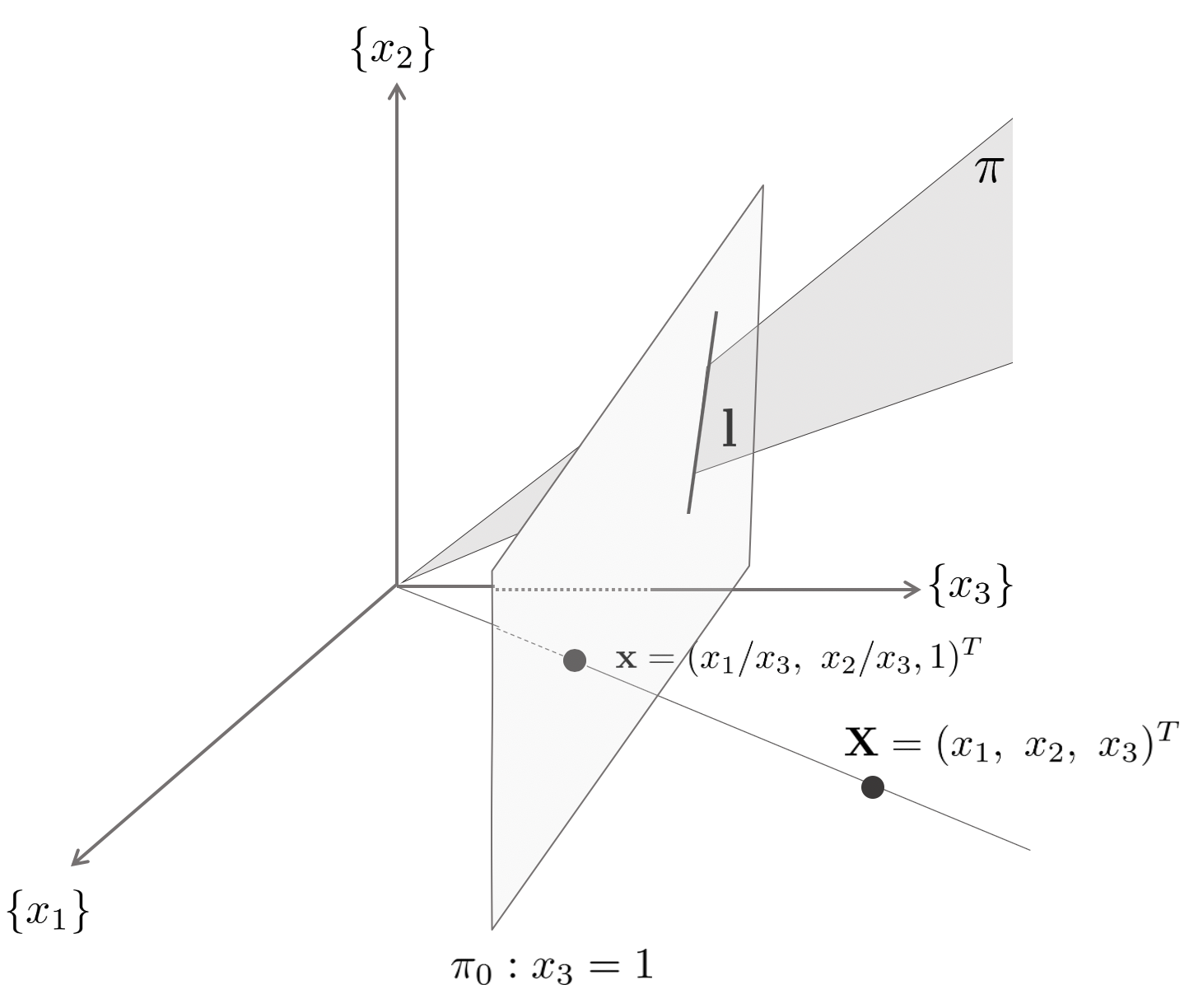
• $\mathbb{R}^2$을 생각하는 방법 중 하나는 $\mathbb{R}^3$의 rays의 set이라 할 수 있다.
• $\mathbb{P}^2$의 직선 l은 $\mathbb{R}^3$ 공간상의 원점을 포함하는 평면 $\pi$에 대응한다.
• $\mathbb{P}^2$의 한 점은 $x_{3}=1$인 평면에서 정의된 (x1/x3, x2/x3, 1)을 대표값으로 이용한다. 이로 인해, $\mathbb{R}^3$에서 정의된 원점을 지나는 직선은 $\mathbb{P}^2$에서 한 점으로 표현된다.

Duality

Reference

• https://edward0im.github.io/mathematics/2020/06/03/multiple-view-geometry1/#org3e4f003