What is Projective Geometry?
실제로 사영변환(projection)을 거치고 나면 몇가지 기하학적 특성이 보존되지 않는 것이 있다. 예를 들면 끝없이 펼쳐진 도로를 찍은 사진이 있다고 하면, 사진에서는 도로의 양끝선들이 끝에서 만나는 것처럼 보이지만 실제로는 만나지 않는다. 유지되지 않는 기하학적 특성들은 다음과 같다
- 원은 타원으로 투영될 수 있다
- 평행선은 무한대의 점에서 만난다
- 직사각형이 평행사변형으로 투영될 수 있다
실제로 angles, distance, ratio of distance는 projection을 거치면 유지되지 않는다고 한다.
반면에 유지되는 특성으로는 직진성(직선은 직선으로 유지)이 있다.
따라서 projective transformation은 straight lines을 유지하는 mapping이라 볼 수 있다.
Homogenous coordinate
- Homogenous 좌표계로 정의된 는 Cartesian coordinate의 에 대응된다.
- (x,y,k) (k=0)은 infinity의 점에 대응된다. 이 무한대를 나타내기 때문이다. 실제, 카르테시안 좌표계로 무한대로 나타내는건 불가능하기 때문.
- 일반적으로 (n차원의 유클리디안 공간)은 (homogenous vectors)로 이뤄진 projective space로 확장될 수 있다
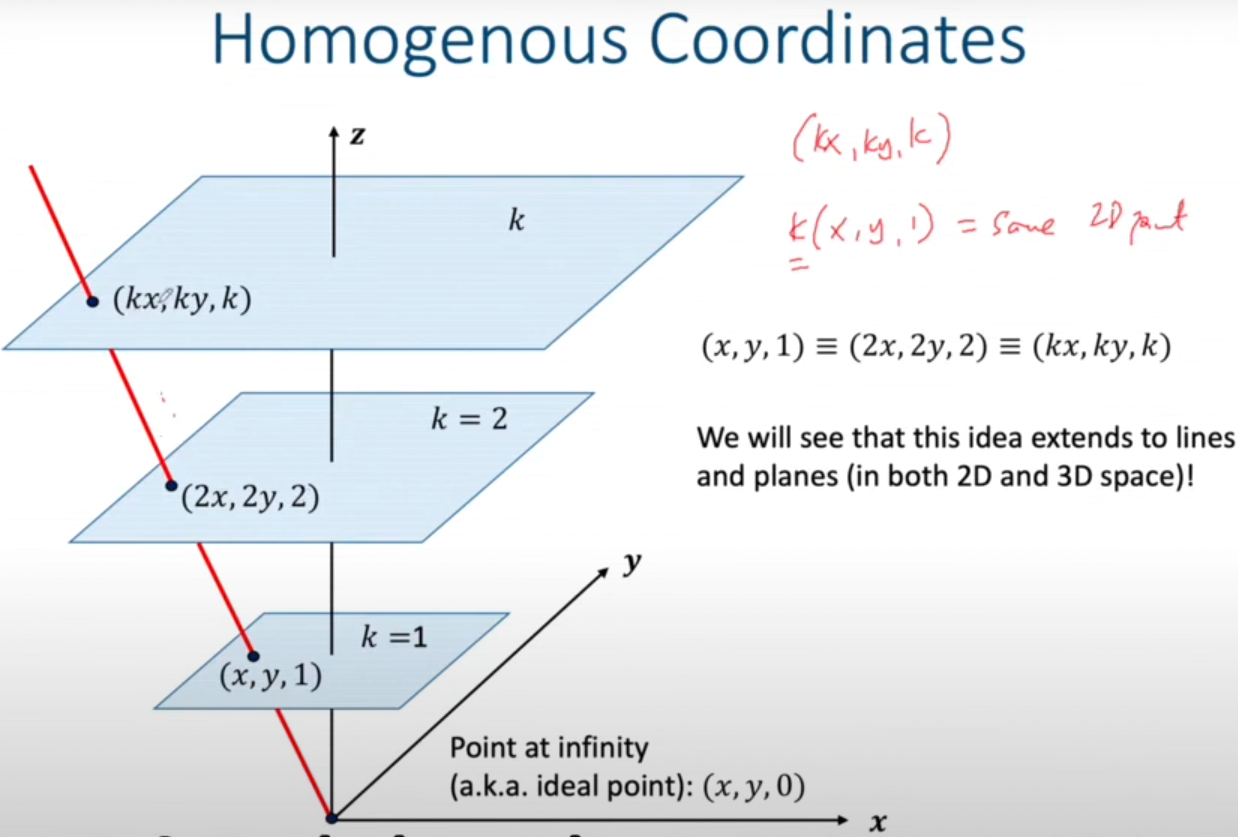
- Homomgenous 좌표계를 사용하면 같은 ray상의 있는 모든 점을 나타낼 수 있다는 장점이 존재한다.
- 카르테시안 좌표계는 일때의 Homogenous의 (x,y,1)으로 나타낼 수 있는 것 같다
The 2D Projective Plane
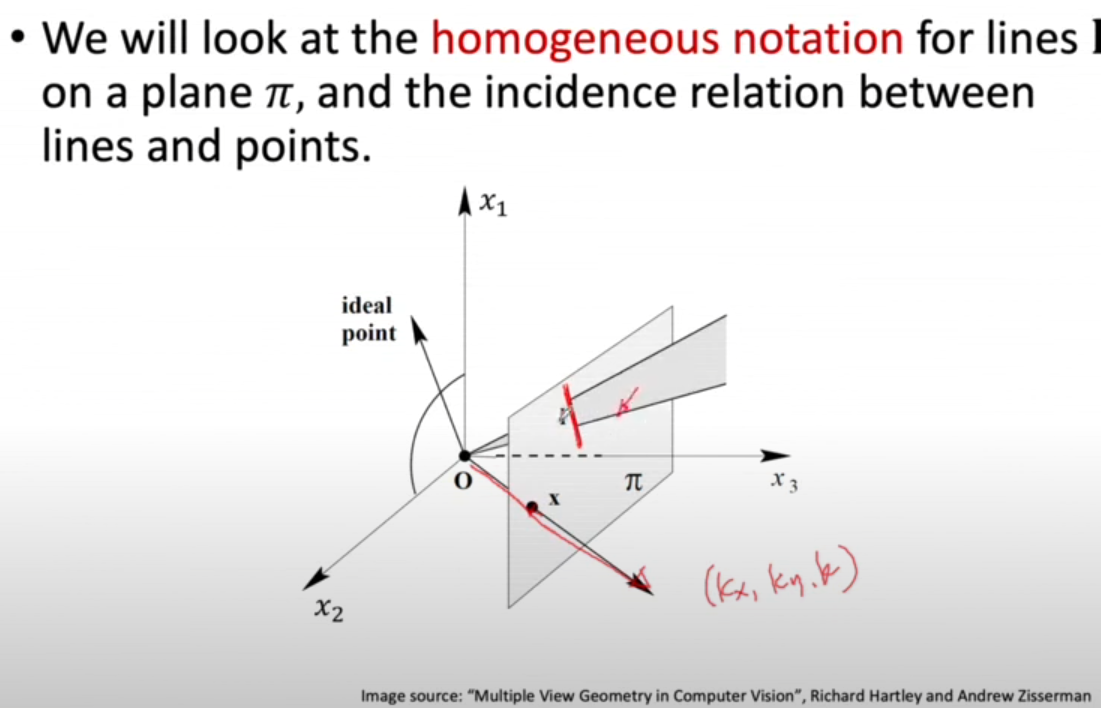
위 그림을 살펴보면, plane 에서 정의된 직선 은 사실 projective space에서는 평면이 된다. 즉, 평면이 plane 에 투영된 것이 직선 이라고 할 수 있다. 또한 plane 위의 점 x는 Projective Space에서는 ray를 의미한다.
Homogenous representation of Lines and Points
평면에 있는 직선은 다음과 같이 표현할 수 있다. . a,b,c 값에 따라 서로 다른 직선이 결정되며, 결국 직선은 vector 로 표현된다.
-
과 은 같은 표현이고, 이는 같은 직선을 나타낸다.
벡터 벡터는 line에 대응되지 않는다. -
직선 에 점 가 지난다고 하면, 을 만족하며 으로, 즉 express할 수 있다
-
유사하게, non-zero k에 대해서 으로 표현된다.
Intersection of Lines
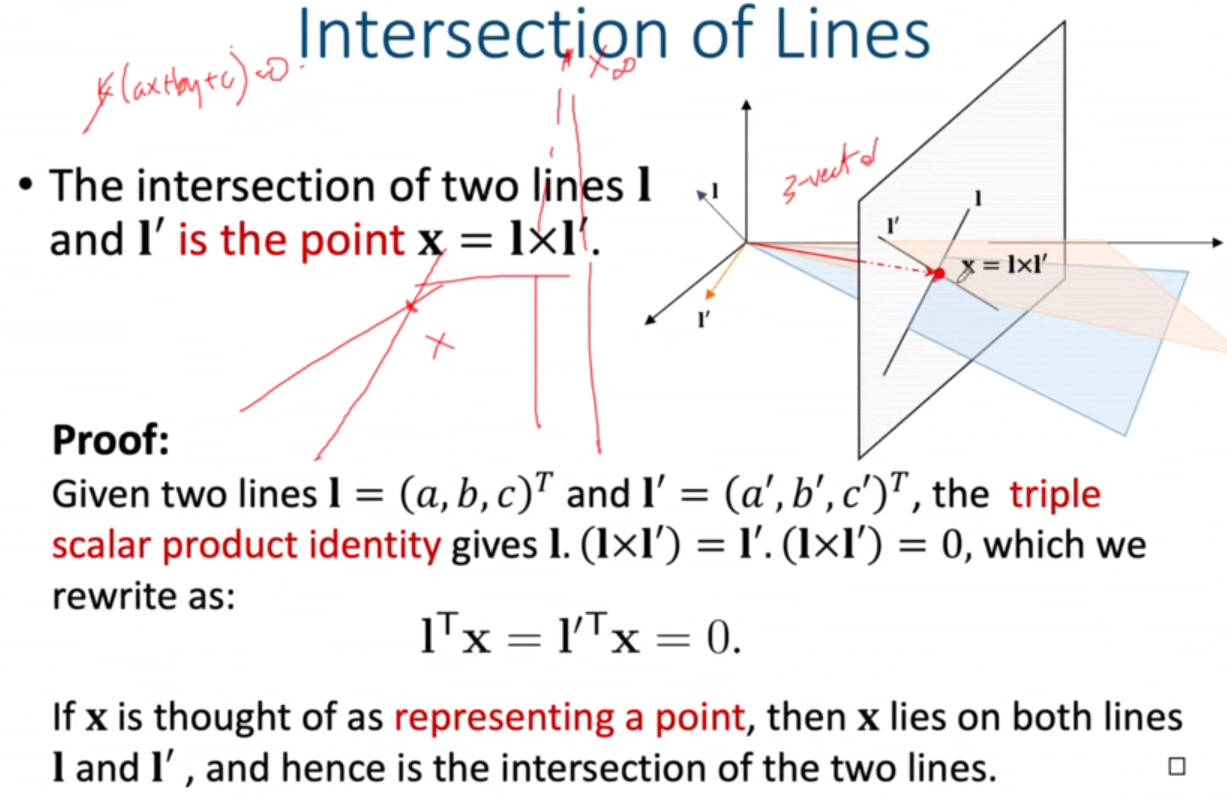
두 직선 이 점 x에서 그림처럼 만난다고 한다. 을 back-projection하면 각각 평면을 나타내게 된다. center에서 x를 있는 ray는 두 평면이 만나는 교선과 같으며, 의 외적값으로 x벡터로 나타낼 수 있다.
-> : vector x와 두 직선 방향벡터는 수직하다!
Line Joining Points
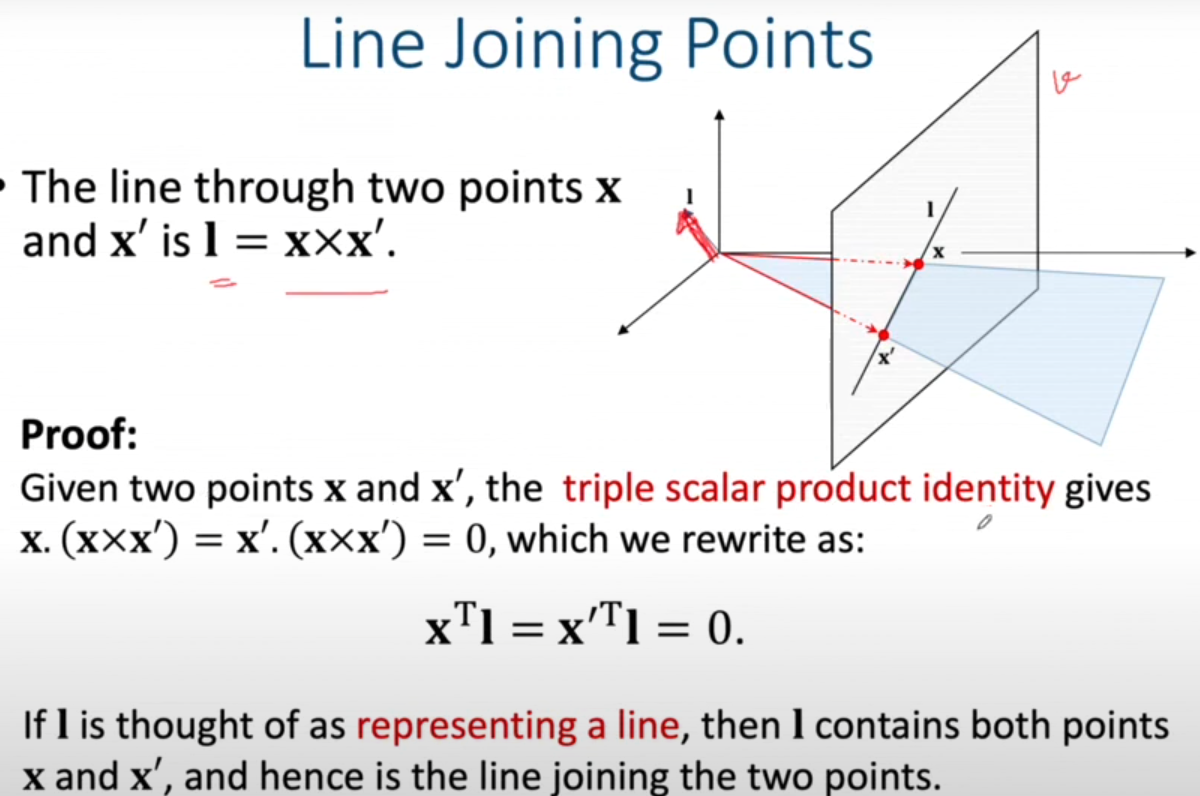
line 이 두점 을 지난다고 할때, 앞서 점이 직선을 지나면 이 유도된다. 따라서 직선 은 벡터 x, x'의 외적으로 나타낼 수 있다.
Intersection of parallel lines
두 개의 평행한 직선 가 있다고 하면, intersection x는 l과 l'의 외적으로 구할 수 있다. 이고, 은 무한대의 점을 가리키고 평행한 선은 무한대에서 만난다.

위의 예시를 살펴보면, x=1과 x=2는 무한대의 점에서 만난다. 실제로 외적값의 결과는 (0,1,0)이며 이는 y축 방향과 같음을 알 수 있다. 즉, y축방향의 infinity에서 두 선이 intersect하는 것을 나타낸다
-
와 는 무한대에 존재하는 ideal point 에서 만난다.
-
inhomogenous notation 는 line과 평행한 방향을 나타내며, (a,b)는 line과 수직한 방향을 나타낸다
Duality Principle
먼저 point와 line의 수식은 다음과 같이 interchange할 수 있다. (점이 선을 지날때), (두 선의 교점) (두 점을 지나는 선). 이와 같이 공간에서는 점과 직선이 동일한 공식에 대해 위치를 바꾸어도 성립하는 대칭성을 가진다. 즉, 두 점을 통과하는 직선의 공식은 두 직선이 교차하는 한 점의 공식과 대칭이다.
Conics and Dual Conics

코닉은 평면에서 이차식으로 정의된 곡선을 의미한다. 종류는 위와 같이 3종류가 있다고 한다. 원뿔과 평면의 intersection이 코닉으로 나타나는 것이다.
코닉의 방정식은(2-degree) 다음과 같이 작성할 수 있다
(non-homogenous)
(homogenous: x->, y->)

점 를 지나는 conic에 의한 conic coefficient는 위와 같다. 5-points에 대해서 stacking하여 식을 얻어 coefficient를 구할 수 있다.

코닉과 점 x에서 접하는 직선 은 이다. 증명은 위의 내용을 참고.
Planar Projective Transformations
2D Projective geometry는 변환 후에도 불변한 성질에 대한 study이다. Projectivity는 -> invertible mapping h을 말한다.
예를 들어 h(x1), h(x2), h(x3)가 동일한 선에 있으면, 점 x1, x2, x3도 동일한 선에 존재한다. projectivity는 colineation이라고도 불리며, projective transformation 혹은 homography라고도 불린다.

x1, x2, x3가 한 직선 l에 있다면, 을 만족하며, H를 non-singular한 3x3 행렬이라 하면, 을 만족한다. 이 식을 통해 point 는 line (inverse mapping)을 지나는 것을 알 수 있다. 따라서 변환하더라도 colinearity가 보존되는 것을 알 수 있다

->이기 떄문에, x'=Hx로 나타낼 수 있으며, H의 특징들로는
1. Non-singular 3x3 matrix(이 존재)
2. matrix element의 ratio가 중요
3. 8-DOF를 가진다.
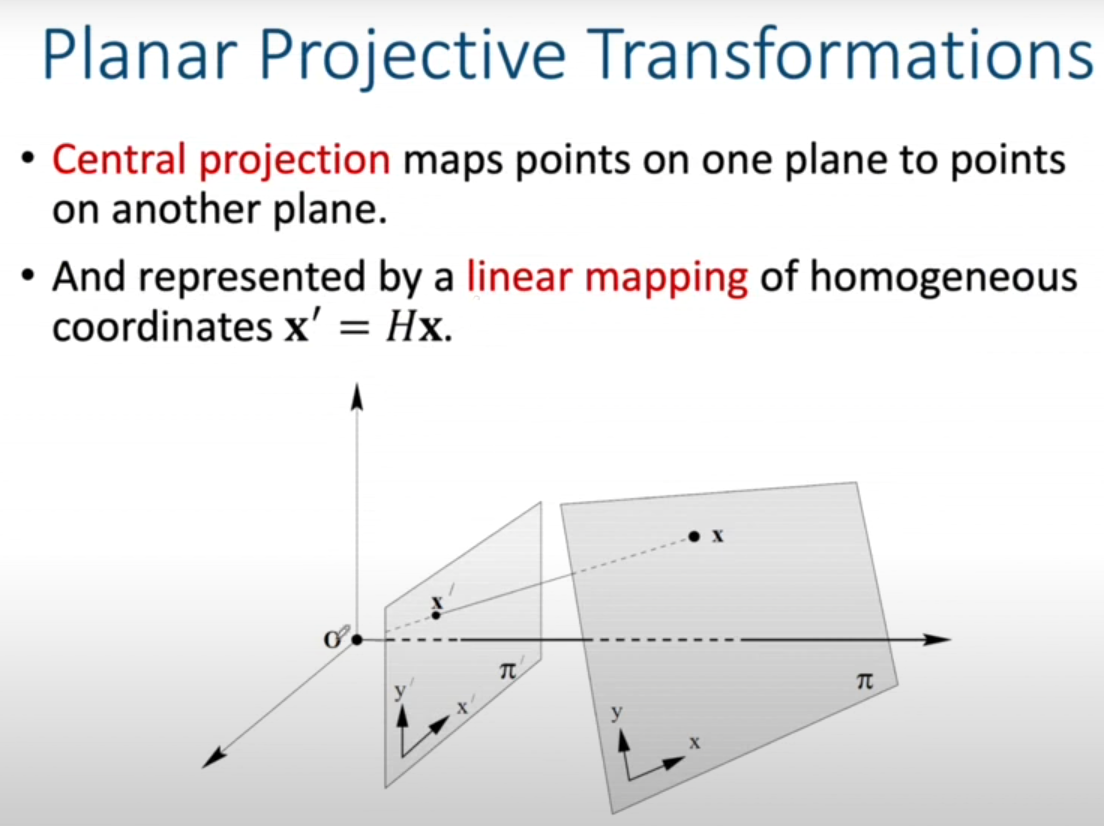
Central projection은 한 평면의 점을 다른 평면의 점으로 mapping하는 것이다. 두 평면의 점 x,x'의 관계는 linear mapping으로 표현할 수 있다
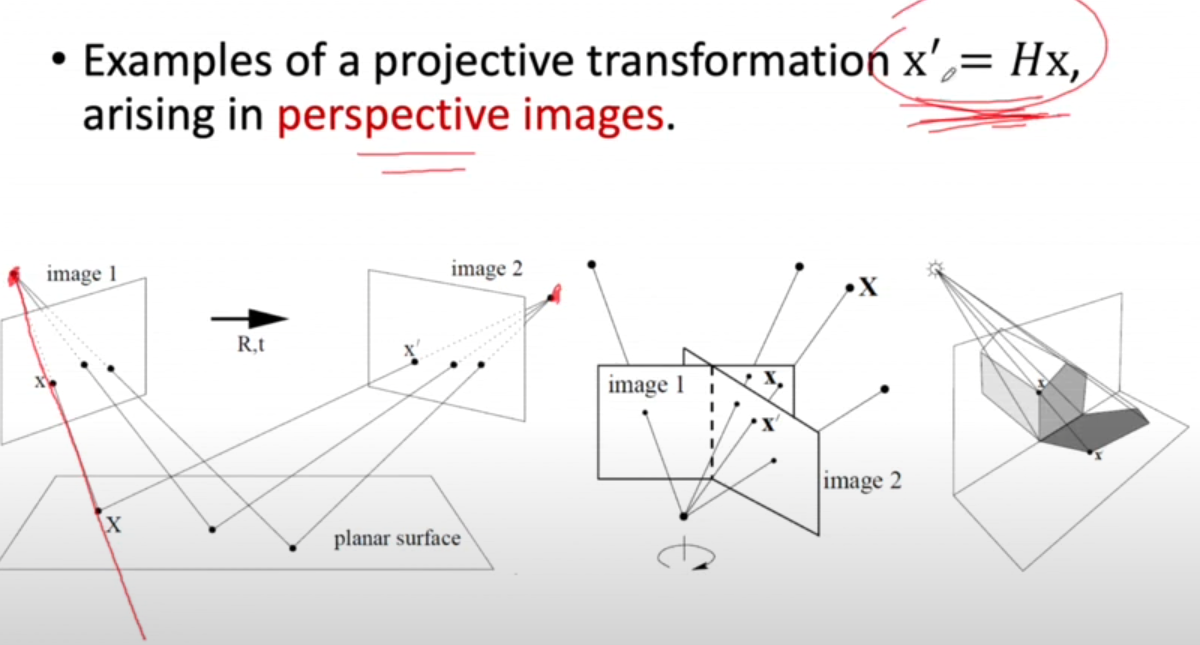
위 그림은 Homography 예시이다. 일단 2가지 전제조건이 있는데 image1의 point가 image2에서도 관찰되어야 한다는 것과, perspective images (rays이 한점에서 모임)다는 전제가 있어야 한다.

점 가 직선 을 지나친다면, 변환된 점 들도 을 지난다. 즉 점위에 직선이 지난다는 것은 변하지 않는다.
이라면, line transformation은 혹은 로 나타난다.
Hierarchy of Transformations: Isometrics
projective 변환은 변환 전과 후 사이에 어떤 성질을 보존하느냐에 따라 여러 종류의 변환 행렬이 존재한다.

Isometries
Isometries 변환은 변환 전후의 Euclidean 거리(물체의 크기)가 보존되는 변환을 말한다.

Similarity
Similarity 변환은 "shape"이 보존되는 변환이다. 는 4자유도(3 isometry + 1 scale)을 가지며, 2점간의 대응관계로부터 계산이 가능하다.
Angles, ratio of two lengths and ratio of areas는 보존된다
Affine
Affine변환은 rotation에 제한이 없어진 isometry 변환이라 할 수 있다. 따라서 roatation 행렬의 자유도가 증가해 총 6-DOF를 가지며, 이로 인해 물체의 크기도 달라질 수 있다.

Affine 변환은 2개의 회전행렬과 skewing 역할을 하는 diagnol matrix의 곱으로 나타낼 수 있다. 아래 그림은 이를 시각적으로 보여준다.
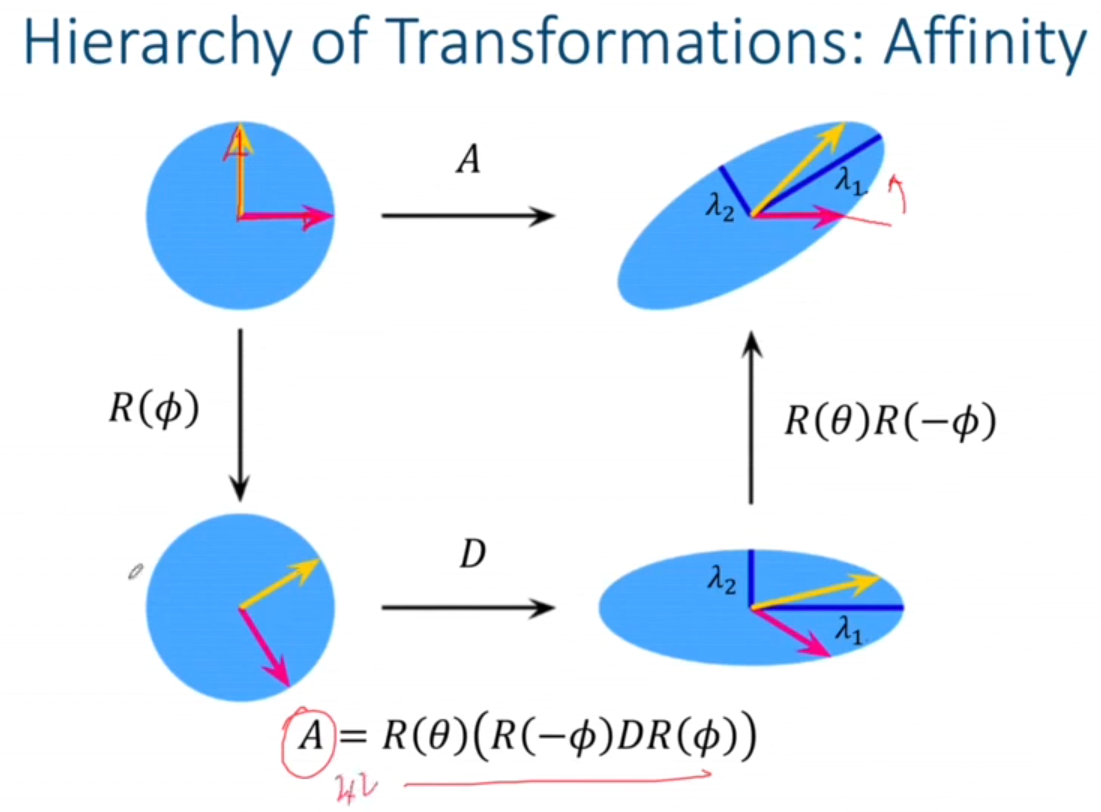
Projective
Projective 변화는 homogenous 좌표계를 변환하는 것으로, 직선을 직선으로 유지한다는 성질을 제외한 모든 것이 유지되지 않는다. 총 9개의 변수가 있지만, ratio가 중요하기 때문에 8-DOF를 가지게 된다.

Decomposition of Projective Transformation
Projective 변환은 앞서 언급된 변환들의 chain으로 정의할 수 있다.
A(어파인 행렬): , K는 det(K)=1로 정규화된 행렬
decomposition은 v가 0이 아닐때 가능하다.
Projective Geometry of 1D line
선 에 있는 점을 homogenous 좌표로 표현하면 이다. 이때, x2=0이면 ideal point를 가리킨다. 행렬은 scale을 고려하지 않으면 3자유도를 가지며, 3점을 통해 계산이 가능하다.

summary
- Euclidean, Projective geometry에 대해 설명
- Homogemous 좌표계를 이용하여 points, lines, conics를 표현
- duality relation을 이용하여 line과 point의 관계를 표현
- hierarachy of transformation을 points, lines에 적용
Reference
- lecutre:
- Image sources: https://edward0im.github.io/mathematics/2020/06/03/multiple-view-geometry1/#org0436097
