[3D Computer Vision, Lecture 2] Rigid body motion and 3D projective geometry
3D Vision Lecture
이번 part 강의의 목표는 다음과 같다
- SE(3) group의 개념과 3차원 공간에서 rigid body transformation의 개념을 알아야한다
- 에서의 평면과 점들을 표현하고, point-plane duality에 대해서 설명한다
- 에서의 선에 대해서 null space와 span matrix 그리고 plucker 좌표계에 대해서 설명한다
- 의 conic을 의 quadratic으로 확장한다
Three-Dimensional Euclidean Space

는 우리에게 친숙한 유클리디안 space로 3차원을 의미하며, 유클리디언 공간에 있는 점은 3개의 카르테시안 좌표계로 나타날 수 있다.
유클리디언 공간에서 벡터()를 정의하자면, point(p,q) pair에 의해 결정되며, 이다. Base vector라는 것도 존재하는데, base 점이 없이 정의되는 경우다.
Coordinate Frames
World Frame(Reference frame)을 기준으로 우리는 rigid-body의 motion(relative pose)를 알 수 있다.

위의 예시처럼 월드 좌표계를 기준으로 rigid body의 중심을 R, T vector로 표현할 수 있다.
Rigid-body motion

Rigid-body motion이란 변환 이후에도 물체(강체)의 변형이 일어나지 않는 것으로, 변환 이후에도 물체의 모양이나 길이는 유지된다.

Rigid-body transformation을 g라고 생각. 임의의 두점 사이의 거리(벡터의 크기)는 rigid-body transformation 이후에도 유지되어야 한다. distance는 유지되지만 방향은 유지되지 않는다
Special Euclidean Transformation
- 변환 후에도 vector의 norm을 유지함과 동시에 cross product의 성질도 유지해야 한다. 이 의미를 살펴보면 거리는 유지되면서도, 외적의 성질이 계속 유지되어야 3축으로 정의하는 것이 여전히 가능해서 그런 것 같다.

Angle이 유지되는 것도 norm이 유지되는 성질로 아래와 같이 살펴볼 수 있다.

Volume 역시 유지되는데, 이는 triple product를 통해 보일 수 있다

Orthogonal Matrix Representation of Rotations
고정된 원점 O에 대해서 rigid object의 회전을 정의핸다고 한다. 즉 물체의 orientation frame을 solid frame에 대해서 나타낼 수 있다고 하자. 아래 그림처럼 g에 의해서 world frame basis vector e1, e2, e3가 각각 r1, r2, r3로 변환된다.

r1, r2, r3는 의 3축에 존재하는 단위벡터이며, orthonormal frame이라 할 수 있다.
Euler Angles to Rotation Matrix
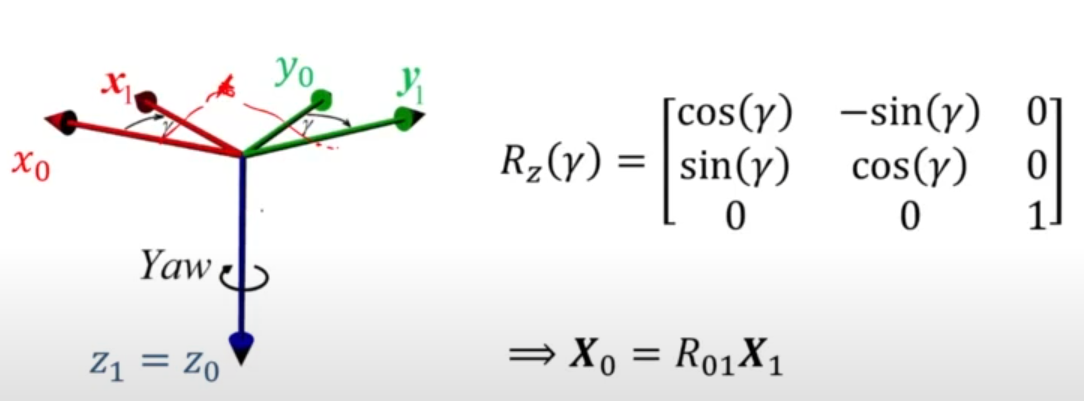
위의 경우는 z축을 따라 yaw angle 회전하는 것이며, 변환 행렬은 위와 같이 정의할 수 있다
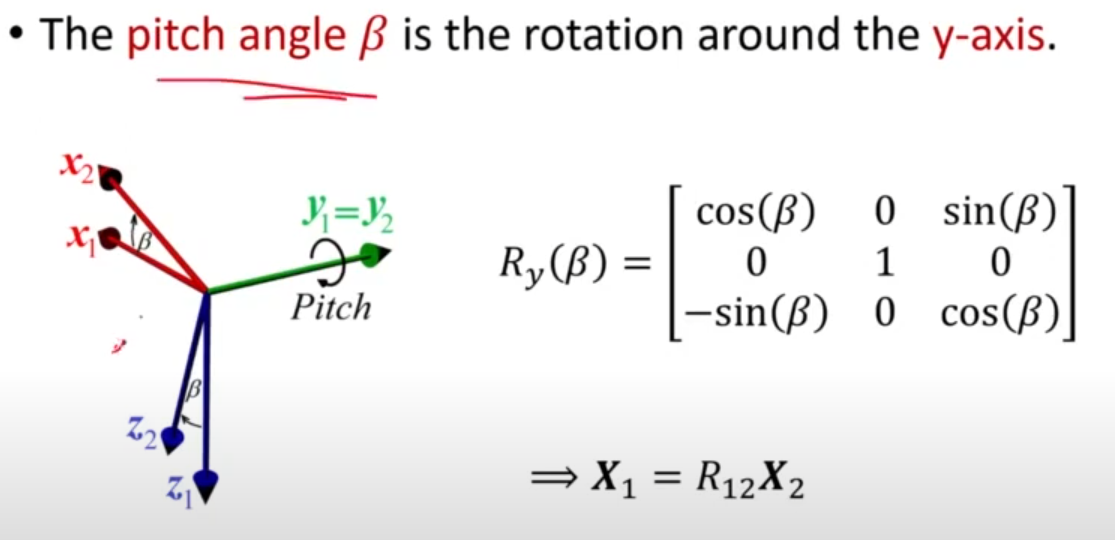
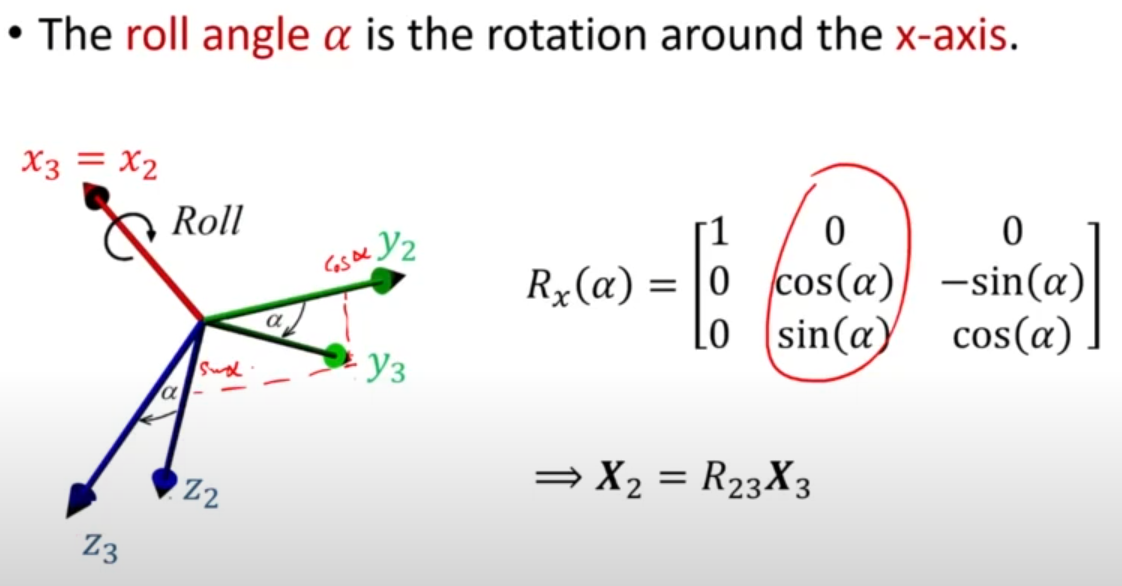
마찬가지로 Pitch와 Roll에 대해서도 변환 행렬을 표기할 수 있다. 이를 종합하여 z-axis, y-axis, x-axis의 결합으로 회전 변환을 나타내면 아래 그림과 같다
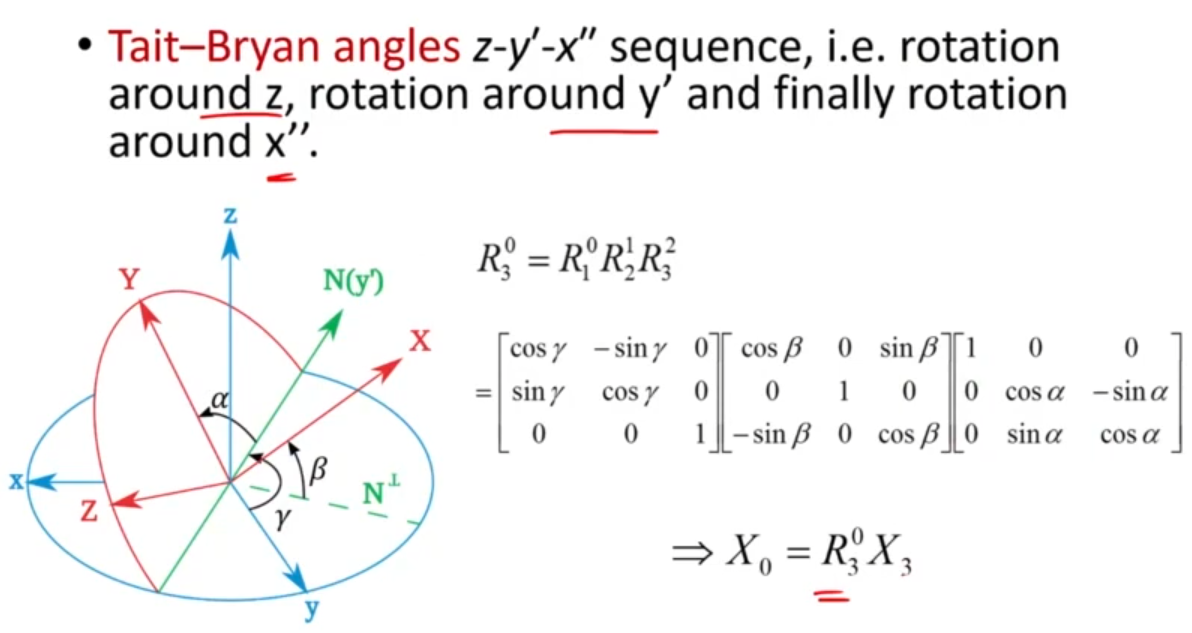
Rigid-body transfomration에서 Camera frame의 축들을 만큼 회전시킨 후에 만큼 이동시켜서 world frame으로 보낼 수 있다. 결국 로 표기 가능하다.

g의 homogenous representation을 이용하면 special Euclidean transformations로 나타난다. 
Composition of Rigid-body Motions
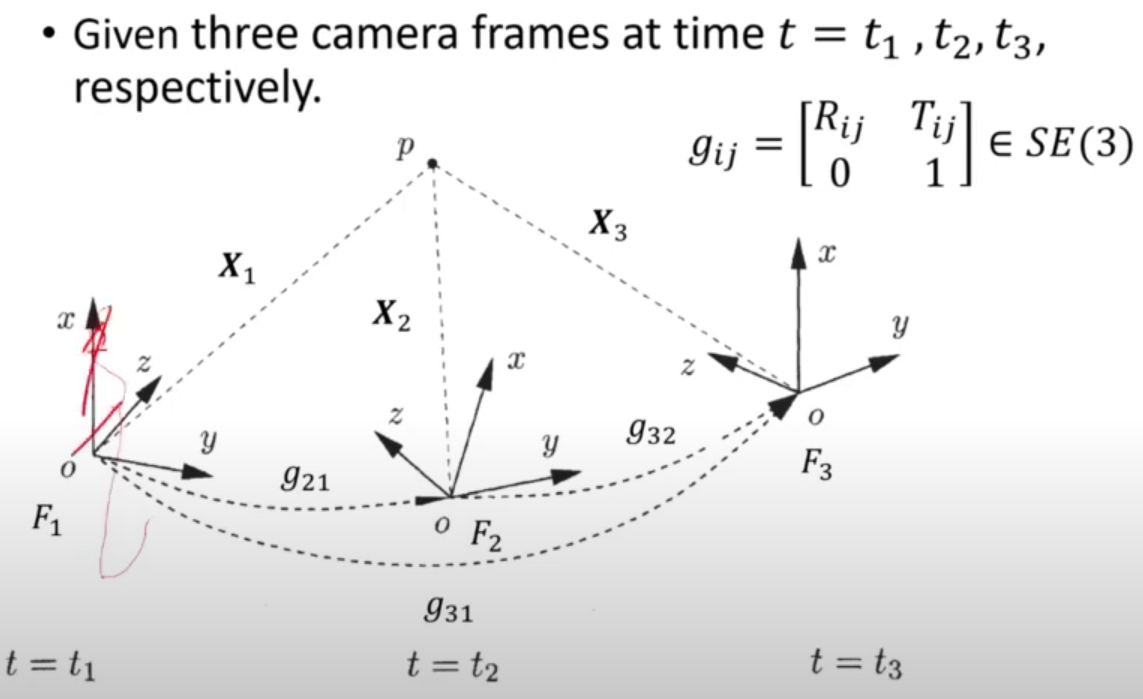
서로 다른 세 시점 t1, t2, t3에서의 카메라 frame을 각각 F1, F2, F3라 한다. 은 F1에서 F2로, 은 F1에서 F3로 transfomration을 해줍니다.
-> F1 Frame에 대해 정의된 좌표를 g21에 의해 F2 Frame으로 나타낼 수 있다
-> F1 Frame에 대해 정의된 좌표를 g31에 의해 F3 Frame으로 나타낼 수 있다

(Composition rule)이 성립한다. 또한 Inverse rule역시 성립하여 를 만족하며, 를 만족한다.
Projective Geometry and Transformations of 3D
의 많은 특성들은 의 straightforward generalization이다. 의 점 는 의 점 로 augment 할 수 있다.
Points in

3차원의 점 X는 와 마찬가지로 homogenous 좌표계로 표현가능하며, 성질 역시 동일하다. 또한 에서의 linear transformation(H)역시 와 동일하게 아래와 같이 표현할 수 있다.

Planes in
3차원 공간에서의 평면은 다음과 같이 서술할 수 있다. . 이를 다시 Homogenizing하여 표현할 수 있다.

의 독립된 비율이 중요하다. 는 특히 plane normal vector를 나타낸다.


3개의 점 가 plane 에 놓여있다고 하면, 평면의 방정식은 을 만족한다. 각 점에 대해 stacking을 하여 3x4 행렬로 표현이 가능하며, 는 점이 서로 다른 위치에 있으면 rank 3를 가지며, linear independent이다.
Lines in
Line은 2개의 점들의 join 혹은 두 평면의 교선으로 이뤄질 수 있다. 3차원 공간에서 Lines은 4자유도를 가지고 있다. 3차원 line의 homogenous 5-vector로 표현하는 것이 어색하지만, 2개의 alternative한 표현방법을 먼저 소개한다

만나지 않는 3차원의 점 A,B가 있다고 한다. A, B 벡터의 span 이용하여 직선을 표현할 수 있을 것이다.


P,Q를 각각 null-space에 대한 기저 벡터라 하면, WP=0을 만족하고, 을 만족하기에, P는 점 A와 B를 포함한다고 할 수 있다. 이는 Q에 대해서도 마찬가지다. A,B는 평면 P,Q에 모두 있기에 W에 의해 정의된 line은 두 평면의 교선이라 할 수 있다.
따라서 두 평면의 교선은 P, Q의 span으로 나타낼 수 있다
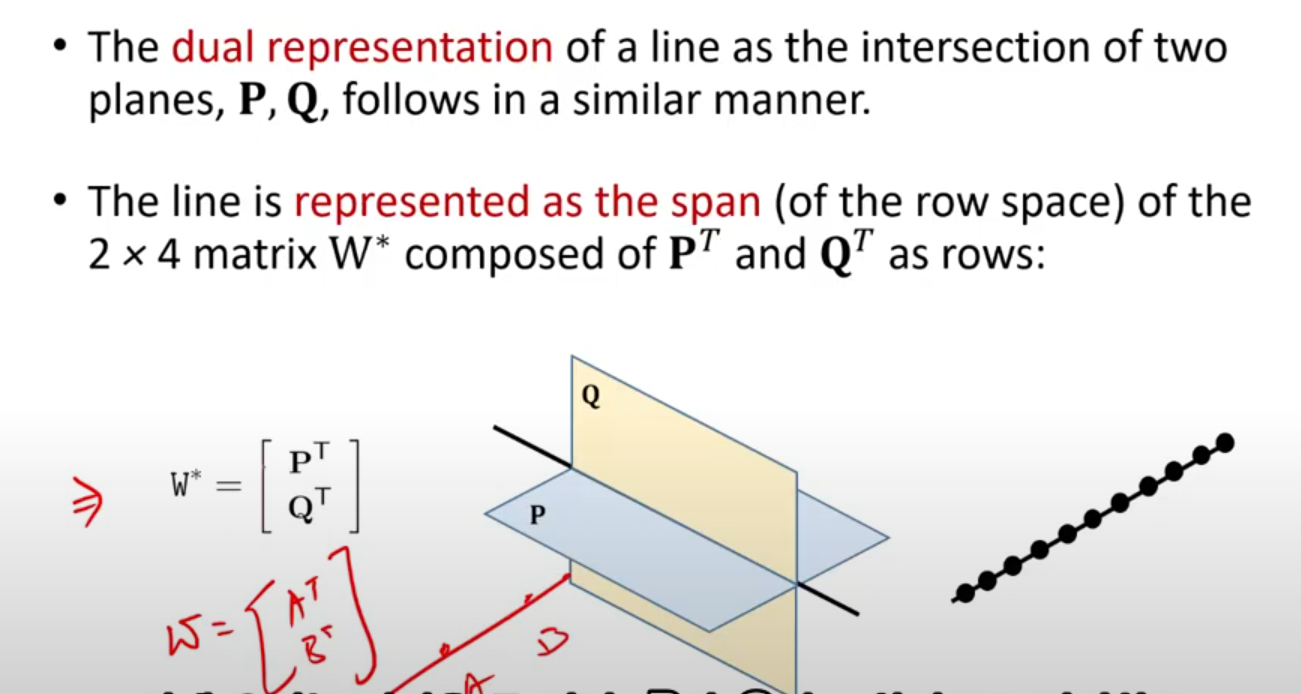
이러한 line의 dual한 표현 방법은 점 A, B를 지나는 직선(span of ) 혹은 평면 P, Q의 교선(span of ) 로 나타낼 수 있다.

평면 위의 점 X와 점A,B를 지나는 선 W가 있다고 하면, 행렬 M을 위와 같이 표현 가능하며 을 만족한다.
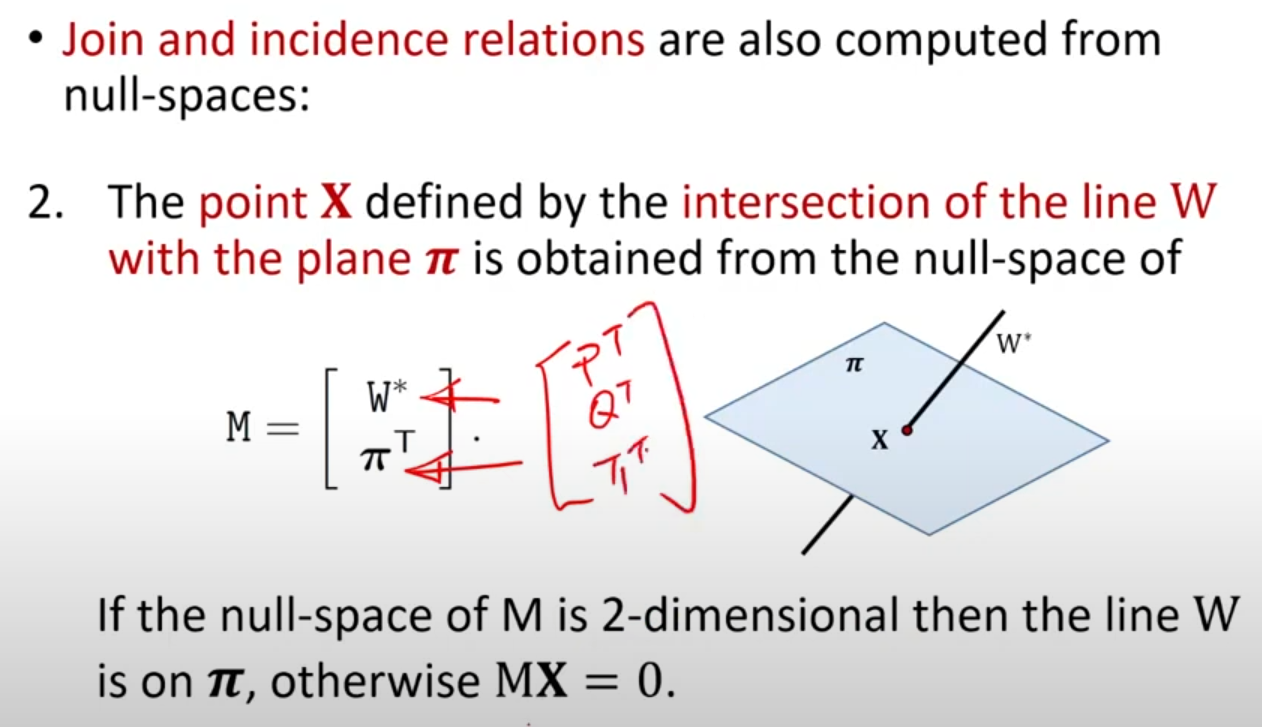
두 평면 P,Q의 교선인 line W와 점 X에 의해 행렬 M이 정의된 경우도 있다.
Plucker Line coordinates

플루커 벡터를 이용하여 직선을 표현할 수 있다. 앞의 3개는 직선의 방향을, 뒤의 3개는 A, B 벡터의 외적을 나타낸 것이다.

평면 P,Q의 교선을 L, 의 교선을 이라 하면, 두 선이 만날 때 위의 식을 만족한다.
