What is camera?
: 카메라란 3D world와 2D image를 mapping하는 과정이다. 이를 projection이라 한다.

Camera models

• 이번 강의에서는 central projection 모델을 탐구한다.

Basic Pinhole Model

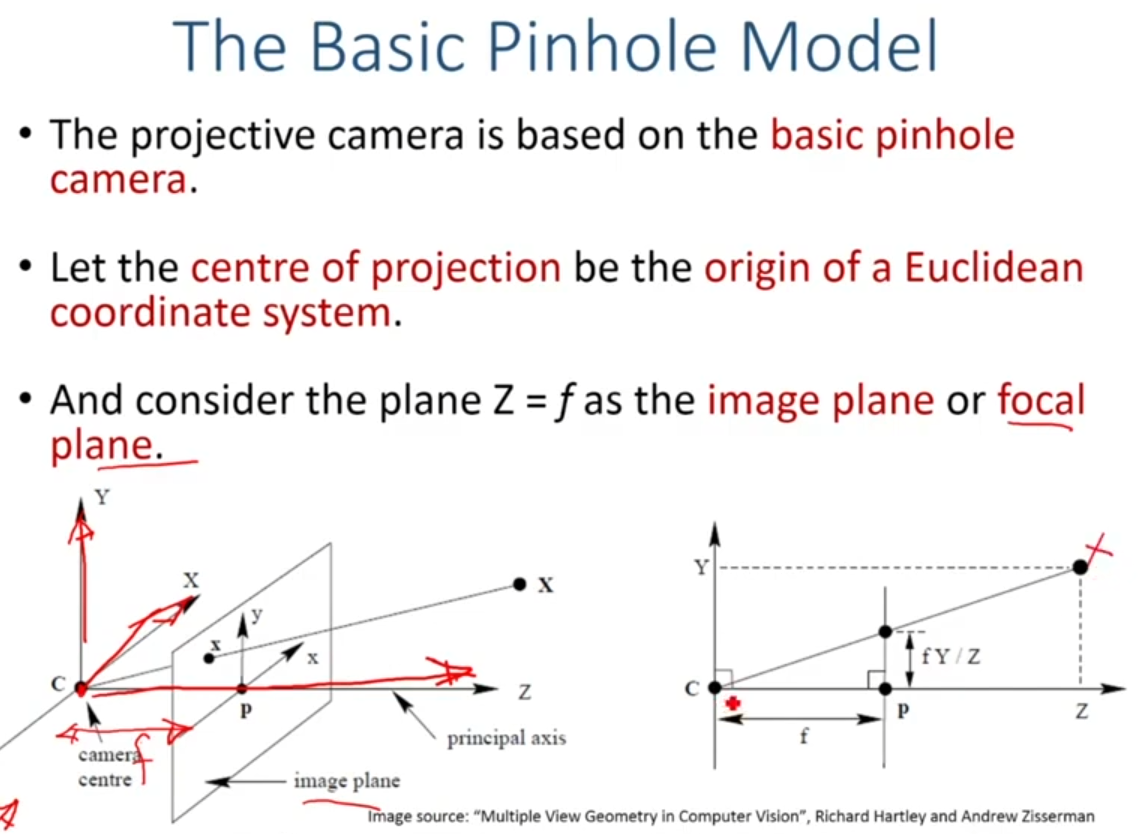
focal length만큼 떨어저 있는 평면을 이미지 평면이라 한다. 닮음 관계를 이용하여 우리는 central projection mapping (3D -> 2D)를 얻을 수 있다.

$(X,Y,Z)^T -> (fX/Z, fY/Z)^T$

Central Projection using homogenous coordinates

focal length만큼 떨어진 점의 X, Y 좌표는 Central projection matrix에 의해 표현될 수 있다.

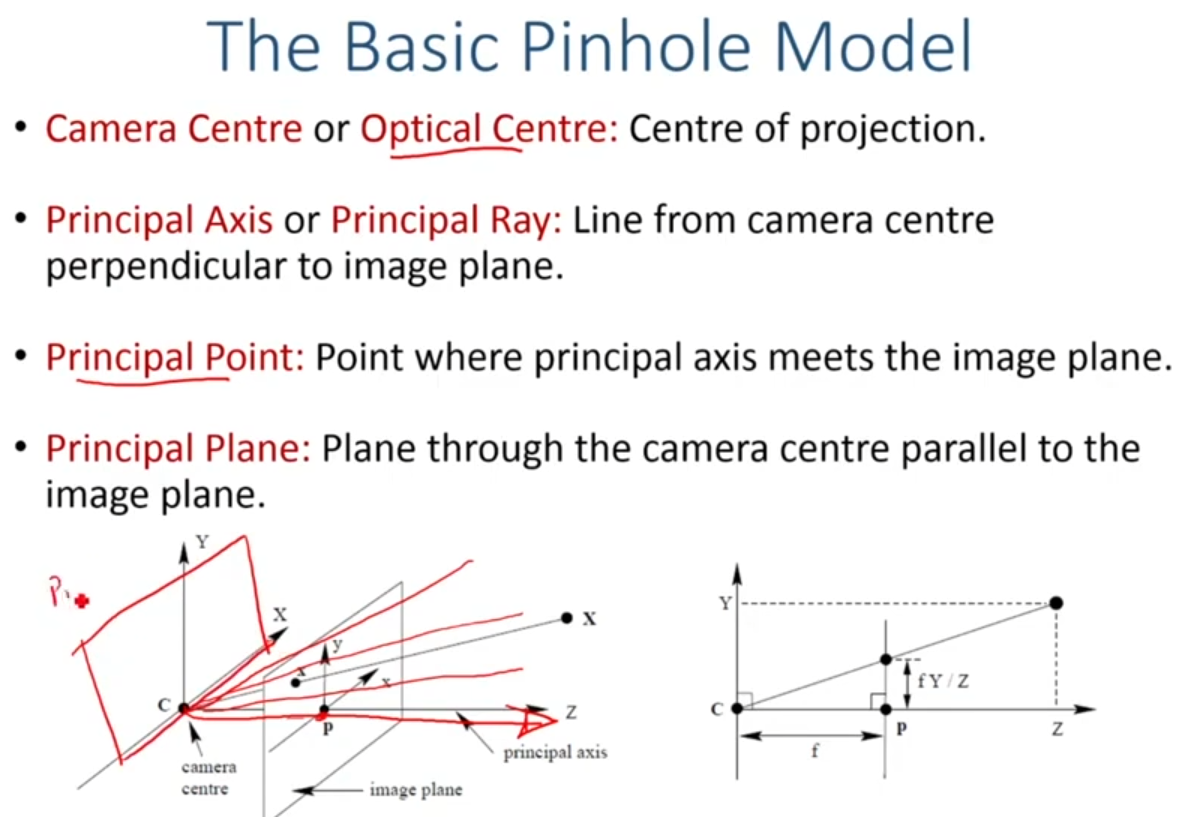
Principal point가 Image plane과 만나는 점이 principal point이고, 이를 offset으로 주어서 표현하면 fX + Zpx, fY + Zpy가 된다.

Projection과 Offset을 한번에 camera calibration matrix K로 나타낼 수 있으며, 0인 성분을 제외하고 3x3 matrix꼴로 나타난다.

World coordinate를 Camera coordinate로 변환하는 것은 Rigid Transformation(R,t)를 통해 가능하다. 이를 Extrinsic Calibration이라고도 한다.

Rotation matrix

X, Y, Z 축 각각에 대한 rotation을 Roll, Pitch, Yaw 방향으로 회전한다고 한다.

Rotation matrix는 2x2 or 3x3 squrae matrix로 표현이 가능하다. matrix의 determinant 크기는 1로 유지되며, 3번째 column의 벡터는 다른 2개 벡터의 외적과 같다.

The basic pinhole Model

P(projection matrix)는 총 9개의 자유도를 가지며, 3개는 K(intrinsic parameter), 3개는 rotation, 3개는 transition이다. 또한 extrinsic을 R,t의 관점으로 쓰는 것이 더 편리하다.

$P = K[R|t], t=-R\hat{C}$

Non-Square and Skewed Pixels

• x, y direction으로 같은 focal length f를 가지는 것을 가정(square pixel assumption)

하지만 실제로 pixel은 non-square하며 real camera에서 skewed 될 수 있다. 따라서 더 정확히 표현하기 위해서는 $f_x, f_y$처럼 각각의 방향마다 다른 focal lengths를 가지며, skew parameter가 있어야 한다.

Intrinsic, Extrinsic 정리

Finite Projective Cameras

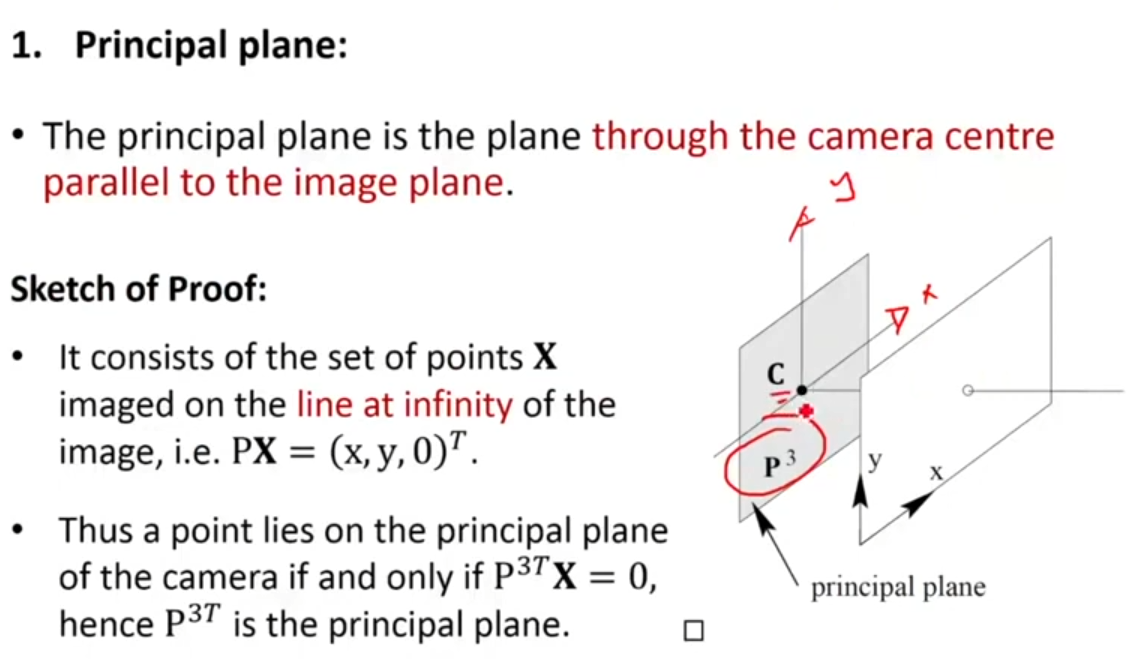
Principal plane이란 이미지 평면과 평행하면서 camera center를 포함하는 평면이다.

Summary of the properties P

Projective Camera on Points

Forward Projection

• 일반적인 projective camera는 space point X를 image point x에 mapping하는 것이다. $x=PX$
• 평면상에서 무한대에 있는 점 $D=(d^T, 0)^T$는 소실점을 의미하며, 이는 아래와 같이 매핑될 수 있다
  $x=PD=[M|p_4]D=Md$
• 따라서 오직 M에 의해서만 영향받게 된다.

Back-projection of points to rays

Ray는 선으로 표현 가능하다. $X(\lambda)=P^+X + \lambda C$.

Ray는 다음의 2가지 점으로 형성된다.
1) Camera center C (PC=0)
2) point $P^+X, P^+=P^T(PP^T)^{-1}$는 P의 pseudo-inverse를 나타낸다.

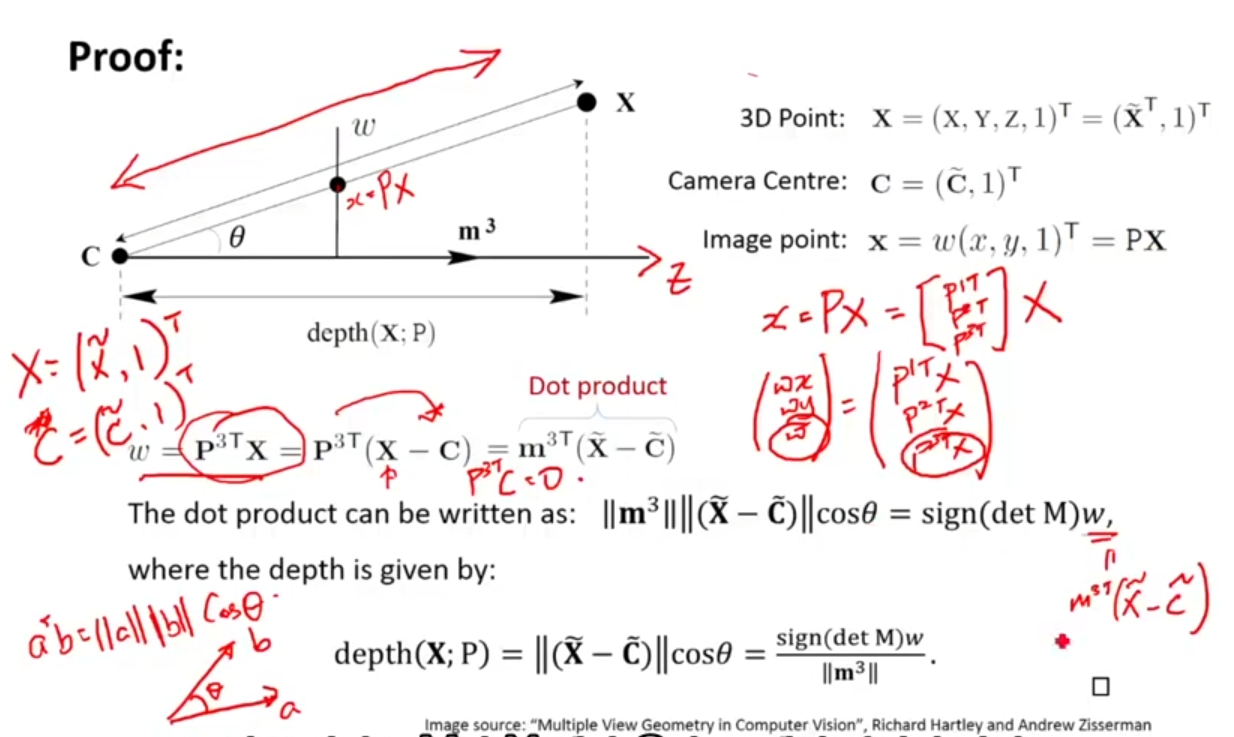
Depth of points

$X=(X,Y,Z,T)^T$가 3D point를 나타내고, P = [M|p4]가 finite camera의 projection matrix라 한다.

$P(X,Y,Z,T)^T=w(x,y,1)^T$라고 가정하면,

$depth(X; P)$ = $sign(det M)w \over{T||m^3||}$

Decomposition of the Camera Matrix

• Given: The camera matrix P
• Find: The camera centre, the orientation of the camera and the internal parameters of the camera

Finding the Camera centre:

matrix M은 KR과 같으며, RQ 분해를 이용하여 KR을 구할 수 있다. 이 떄, K가 positive한 diagnol 값들을 가진다는 제약조건이 있으면, ambiguity는 사라진다.

Intrinsic parameter K의 각각의 성분은 위와 같다.

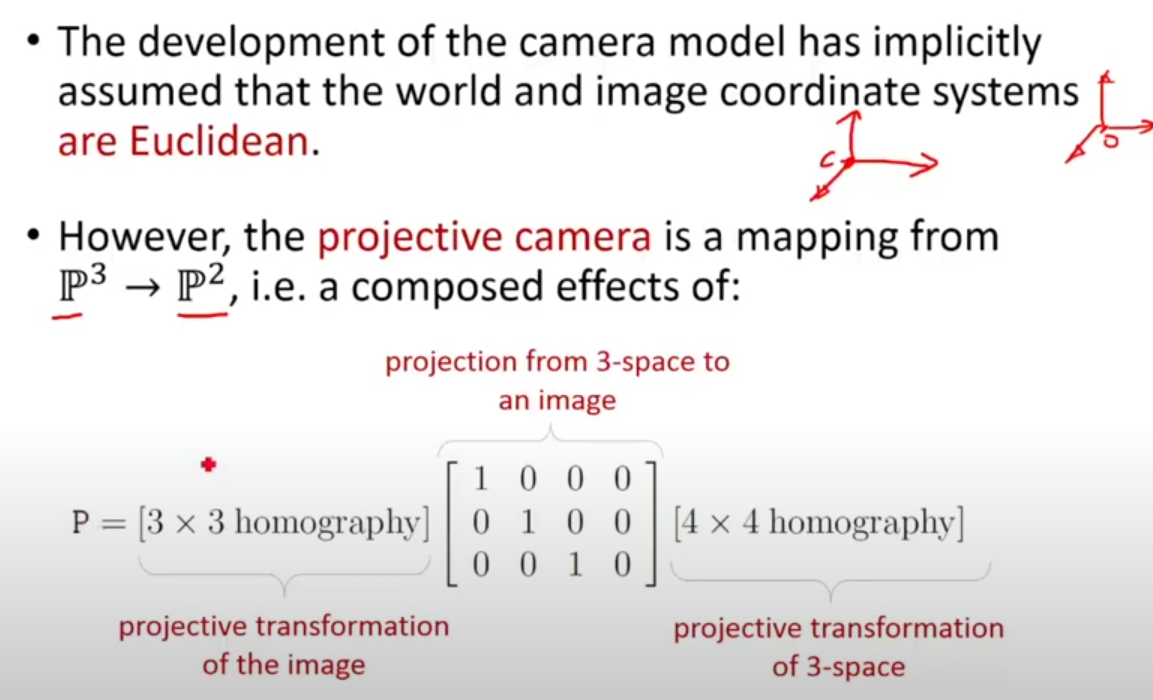
카메라 모델은 기본적으로 world, image 좌표계를 유클리디언 공간에서 정의한다. 하지만, projective camera는 $P^3 -> P^2$로 매핑하는 과정이며, 구성요소는 위와 같다.

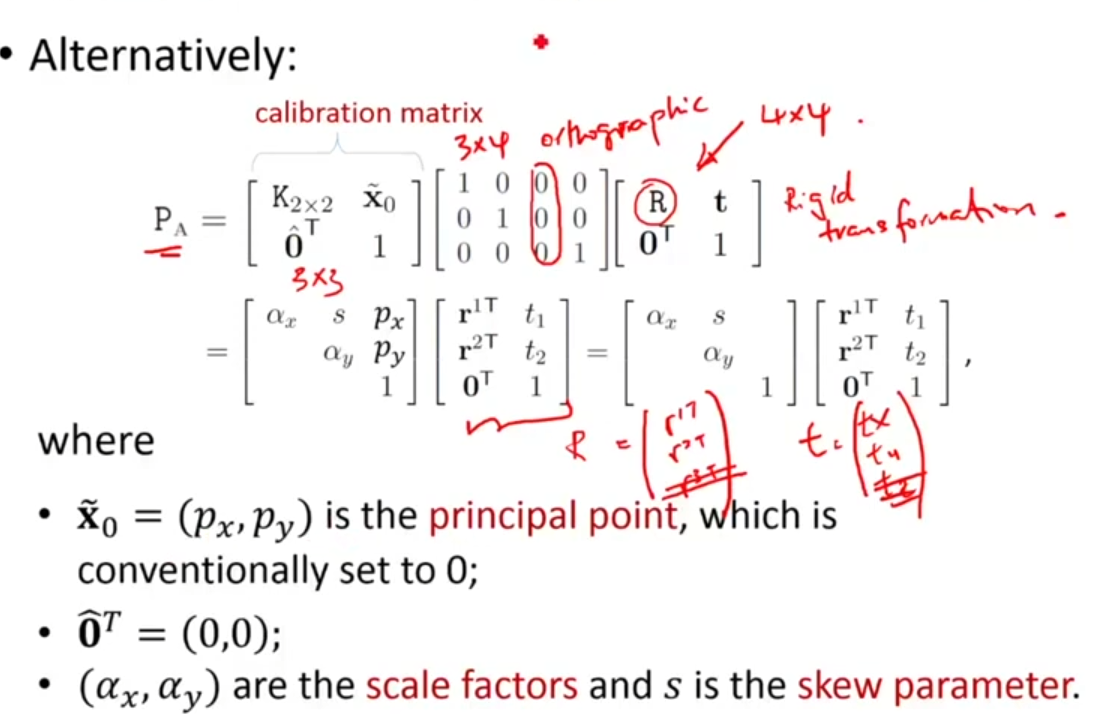
affine camera의 matrix는 위와 같은 form을 가진다.
1) Camera center는 idea point로서, $M_{2\times3}d=0$을 만족
2) $P^{3T}=(0,0,0,1)$은 principal plane으로서, infinity plane위에 놓여야 한다.

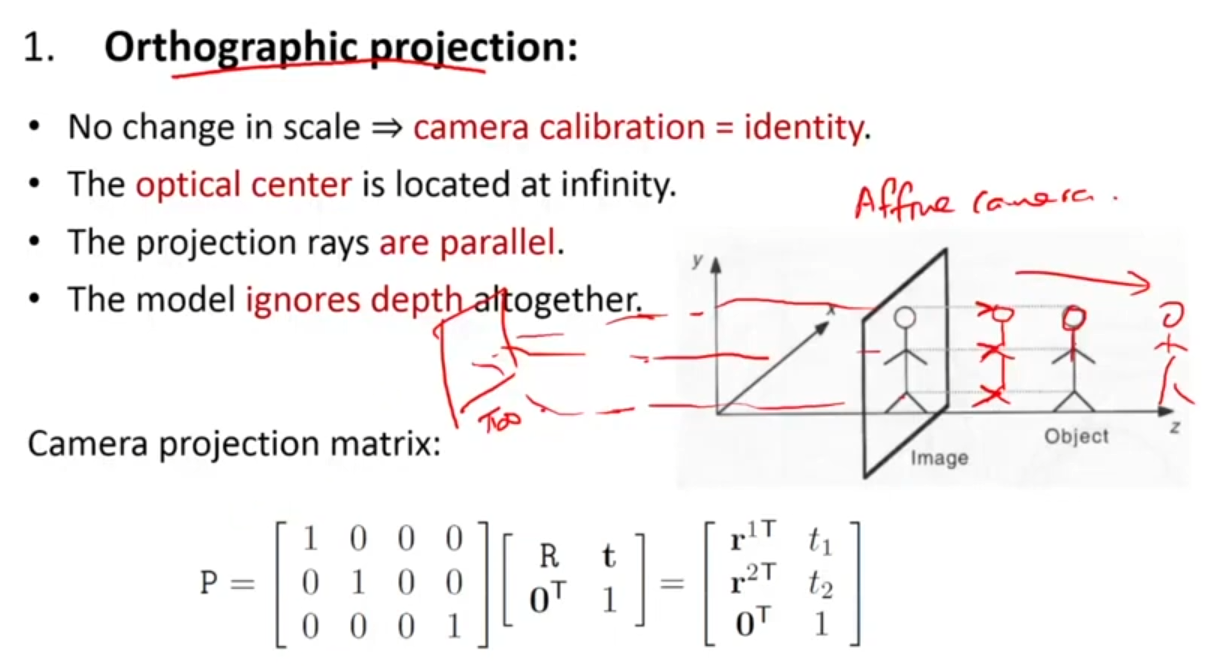
Orthographic Projection

ray가 infinity에 있어서, optical center가 무한대에 존재하고, projection rays이 평행하며, dpeth도 거의 무시하게 된다.

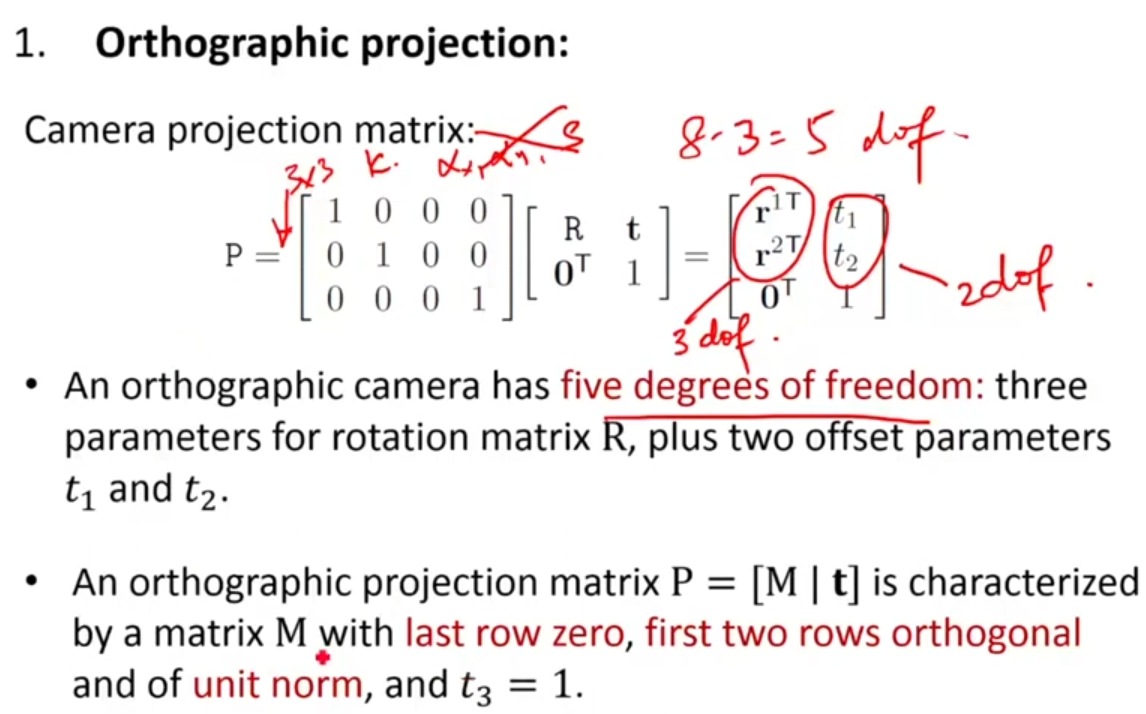
Orthographic camera matrix는 총 5자유도를 가지는데, 3개는 rotations을 2개는 transition을 가진다.

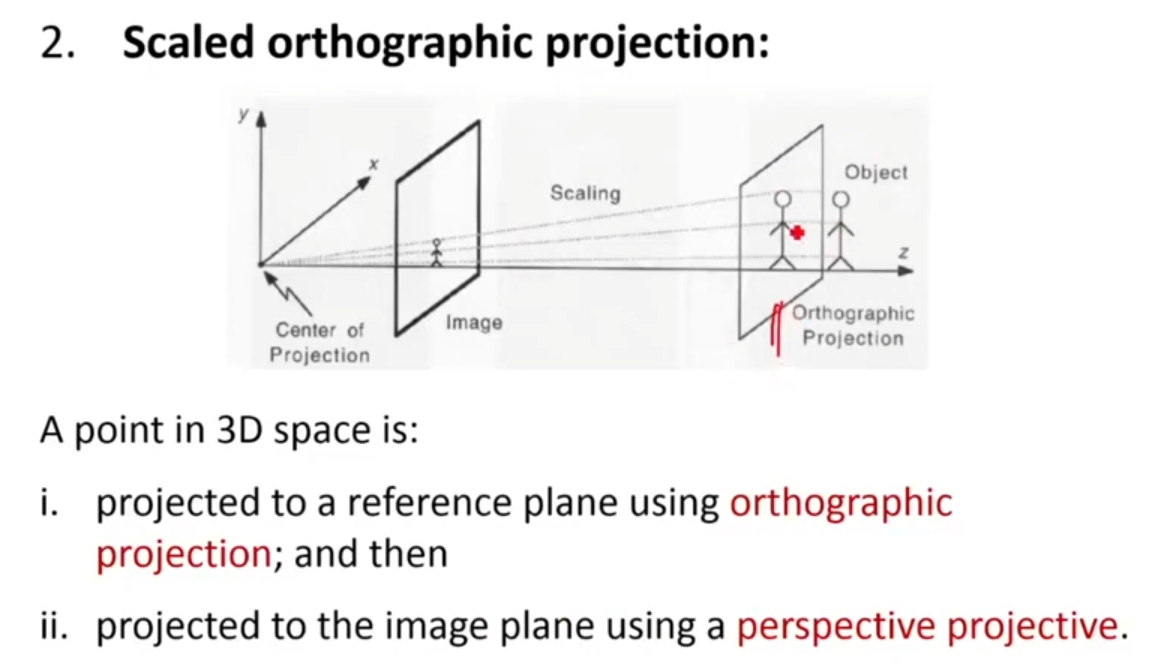
Scaled orthographic projection은 orthographic projection과 perspective projection을 모두 사용한다.