3D Computer Vision Lecture 12 (part1) Generalized Cameras

본 포스트는 NUS대학의 3D Computer Vision 강의 (prof. Gim-Hee LEE)의 강의와 lecture slides의 내용을 인용하였습니다

• 기존의 pinhole camera 모델은 한 점에서 rays가 모임
• 반면에 generalized(non-central) camera는 rays이 모이지 않음
• Generalized camera의 예로는 multiple camera system이 있음

Multi-camera system

• 장점
  1) 가격이 싸고, 유지보수가 쉬움
  2) Field of view가 maxmize됨
  3) Epipolar geometry를 이용하여 Absolute scale을 이용할 수 있음
  
• 한계
  1) 시스템 속 카메라 각각의 카메라를 이용해 독립적으로 계산하여 통합하는 것은 비효율적

Plucker Vectors

• Generalized camera는 모이는 점(refernce point)가 없기 떄문에, 공간에서 임의의 점에 대한 새로운 표현 방법이 필요함.

• line에 대한 플루커 벡터는 3-vectors의 pair로 되어있음. Direction vector $q$(방향)와 moment vector $q'$로 구성

• q벡터는 선의 방향을, q' 벡터는 선에 있는 임의의 점 P와 임의로 정한 reference frame 간의 벡터를 의미. 이는 q와 P의 외적을 통해 구함. 따라서 qTq' = 0(q와 q`은 수직이기 떄문)

• 플루커 벡터를 사용하면, 선에 있는 모든 점들을 위의 수식으로 표현할 수 있음
• 방향벡터(q)는 주로 단위 벡터를 사용하며, 이 경우 qxq`은 선위의 점중에서 origin과 가장 가까운 점이다.

• 다중 카메라 시스템의 경우를 예를 들면, $C_{i}$를 하나의 핀홀 카메라의 origin이라 하면, 이를 플루커 벡터로 표현하면 2번쨰 expression과 같다. 이 때, 방향을 나타내는 벡터 q는 calibartion K의 Inverse로 나타낼 수 있다

• 또한 모멘텀 벡터 q`는 q와 P의 외적으로 구하는데, P를 origin으로 삼으면 결과는 [0,0,0]이 된다

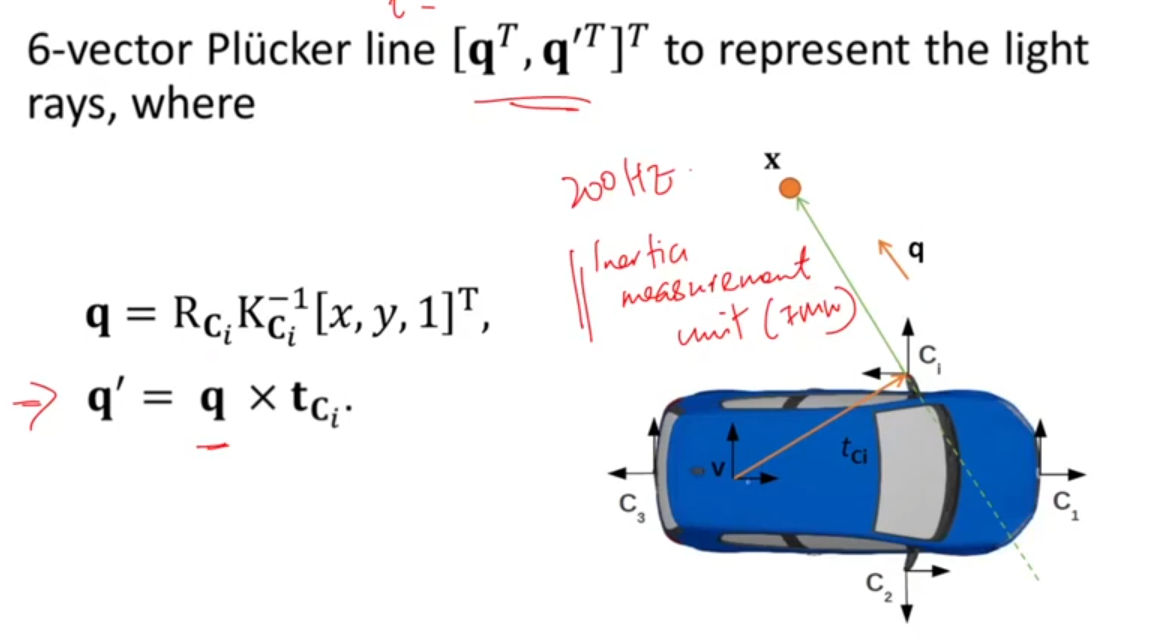
카메라 센터 $C_{i}$가 origin에 있지 않은 경우, 각 카메라에 대한 calibration $K_{Ci}$, origin에서 카메라 센터로 rotation $R_{ci}$, translation $t_{ci}$라 함.

• 다음 경우, $C_{i}$ ray에 있는 특정 pixel의 방향과 모멘텀 벡터를 나타내면 3번째 표현과 같다. momentum 벡터를 $q X t_{ci}$로 나타낸 것은 center를 $t_{Ci}$로 나타낼 수 있기 때문이다.

• 자율주행차의 경우 Inertial measurement unit(IMU)을 origin으로 삼는 경우가 많음.

• 각각의 카메라들의 중심은 IMU로보터 $R_{Ci}, t_{Ci}$만큼 떨어져 있음.

• 각 카메라에 대해 플루커 벡터는 위와 같이 표현될 수 있음

2시점에 대한 Geometry에서 플루커 벡터로 나타내면, 2개의 카메라에서 대응되는 픽셀간의 관계를 안다고 가정.

• 슬라이드의 필기처럼 2개의 ray(플루커벡터)는 공간의 점 (X)에서 만나야 한다

• 카메라간의 relatvie pose(R, t)가 존재

• 첫번째 뷰에서 나타난 $l_{1}$을 두번쨰 뷰의 프레임으로 나타내는 경우, 두 카메라 center의 rigid transformation을 이용하여 위와 같이 $l_{1}$([q1, q1'])을 변환하여 표현할 수 있다

같은 프레임에 있는 2개의 플루커 벡터 line은 한 점에서 교차해야하고, 이는 위와 같은 식을 만족해야 한다.

• 앞서 두식을 연립하여 하나의 식으로 나타내면 위와 같이 되고, matrix form으로 정리할 수 있다.

• 이는 Epipolar Geometry와 유사. 이것을 Generalized Epipolar Geometry라 부른다.
• 총 18개의 변수가 generalized essential matrix에 있음

• 위의 슬라이드 수식(matrix form)을 벡터로 풀어서 식을 정리하면 위와 같이 $a^Tg=0$이 된다

• a는 플루커 벡터로 알려진 elements이고, g는 E와 R에 있는 unknown vector를 가리킨다

• 이를 알기 위해서는 최소 17개의 point correspondence를 알아야하고, 이를 stack하여 $a^Tg=0$ form을 $Ag=0$로 표현 가능

  

• SVD를 통해서 g를 구할 수 있음

Generalized Point Reconstruction

• Triangulation에도 적용할 수 있음.
• 카메라 transformation와 대응점들이 주어진 경우, 점의 3차원 좌표를 구할 수 있다

• 좌변은 $l_{1}$을 R,t를 이용하여 변환한 것
• 우변은 플루커 line($l_{2}$)의 모든 점들을 나타냄
• 3차원 점 P에서 교차하기 때문에, 위의 식이 성립하는 것
• 위의 식은 보통 over-determinate한 linear equation으로 풀 수 있기 때문에, $\alpha_{1}, \alpha_{2}$는 쉽게 풀린다

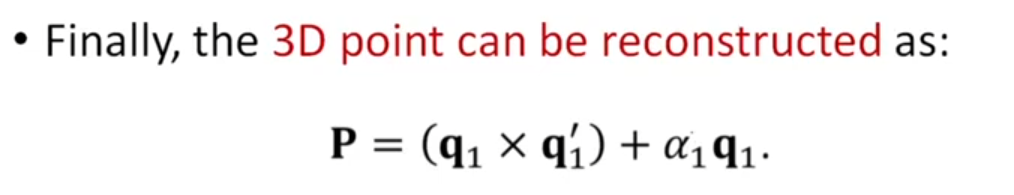
• 3차원 점 P를 1st view 프레임의 플루커 벡터로 나타내면 위와 같이 표현할 수 있다