
CNN
CNN은 초기 신경망의 단점을 해결하기 위해여 도입되었습니다
기존의 Fully-connected-layer 1) 매개변수의 폭발적인 증가 2) 공간 추론의 부족이라는 문제점이 있습니다.
매개변수의 폭발적인 증가
이미지는 엄청난 갯수의 숫자로 구성된 복합적인 구조라 할 수 있습니다(이미지의 높이 X 넓이 X 깊이 (= 채널수, RGB경우에는 3))
앞서 예재로 사용하였던 28 X 28 이미지도 사실 28 X 28 X 1(Grayscale) = 784개의 값으로 이루어진 입력 벡터로 표현할 수 있습니다
또한 네트워크가 깊어질수록 매개변수의 갯수는 매우 증가합니다
공간 추론의 부족
기존의 Fully-connected-layer는 이전 계층의 모든 값을 받기 떄문에 모든 pixel이 원래 위치와 상관없이 결합되므로, 픽셀 사이의 근접성 개념이 손실됩니다
CNN의 도입
CNN은 다차원의 데이터를 처리할 수 있습니다
뉴런이 이전 계층의 모든 요소와 연결된 Fully-connected-layer와 달리,
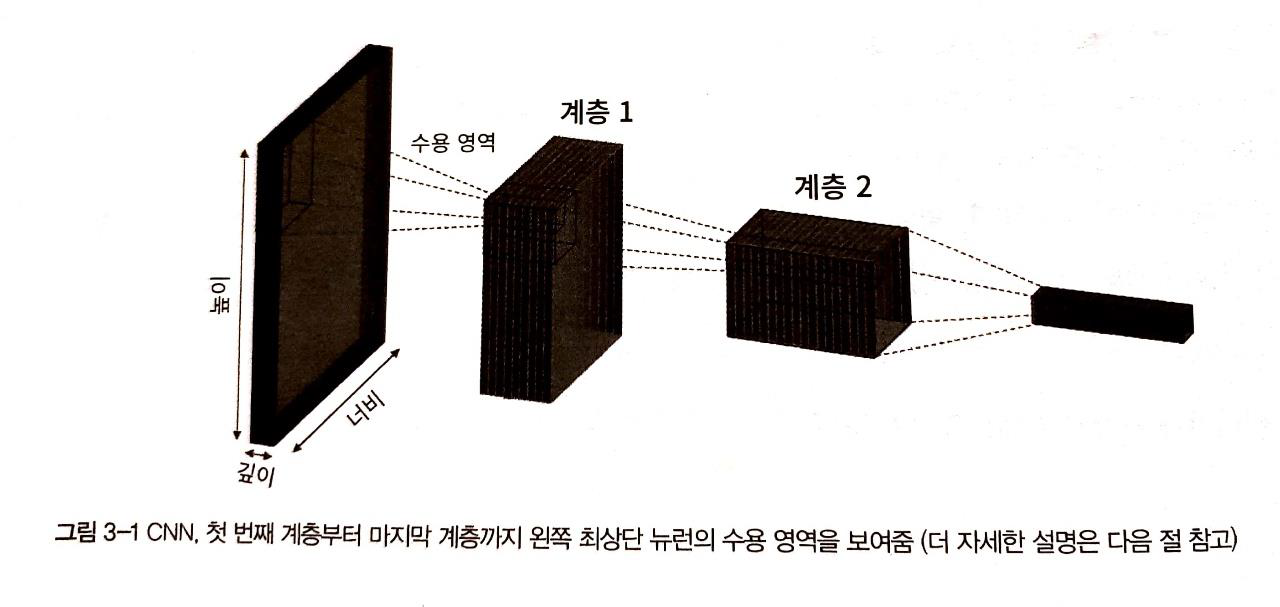
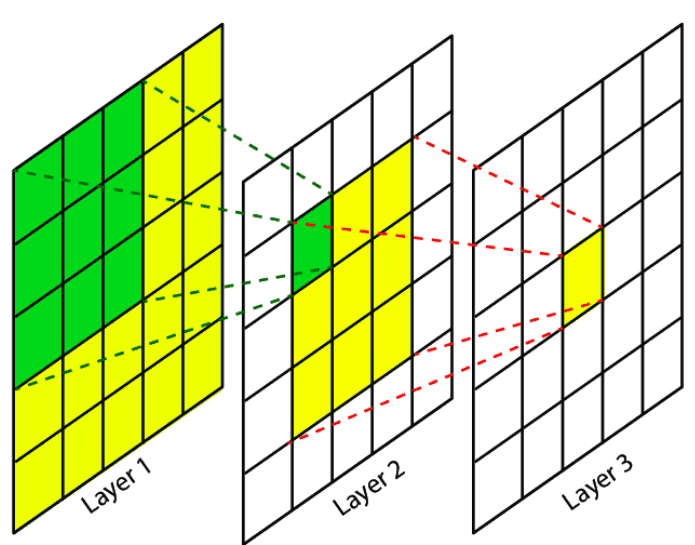
CNN은 이전 계층에서 일부 영역(receptive field라 부릅니다)에만 연결되었다는 특징이 있습니다
아래 그림에서 보다 명확하게 이해할 수 있을 것 같습니다
Convolution과 Cross-relation
: 먼저 Convolution 연산과 Cross-relation 연산을 소개하겠습니다
Convolution과 Cross-relation의 정의는 아래와 같습니다
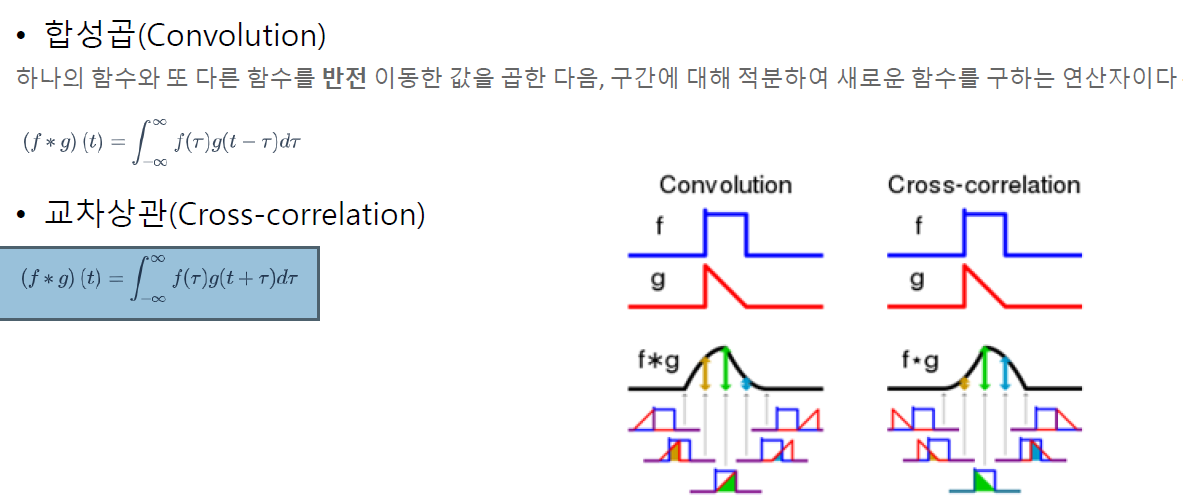
둘의 차이점은 연산 시, filter(위의 그림에서는 함수 g)의 fliping 여부입니다
여기서 우리가 주의해야 할 부분이 있습니다!
머신러닝, 딥러닝에서는 실제로는 cross-relation연산을 실행하지만, convolution 연산이라고 보편적으로 부릅니다. 반드시 알아두세요!
그럼 영상은 2차원이니, 2차원 convolution 연산도 가능할까요?
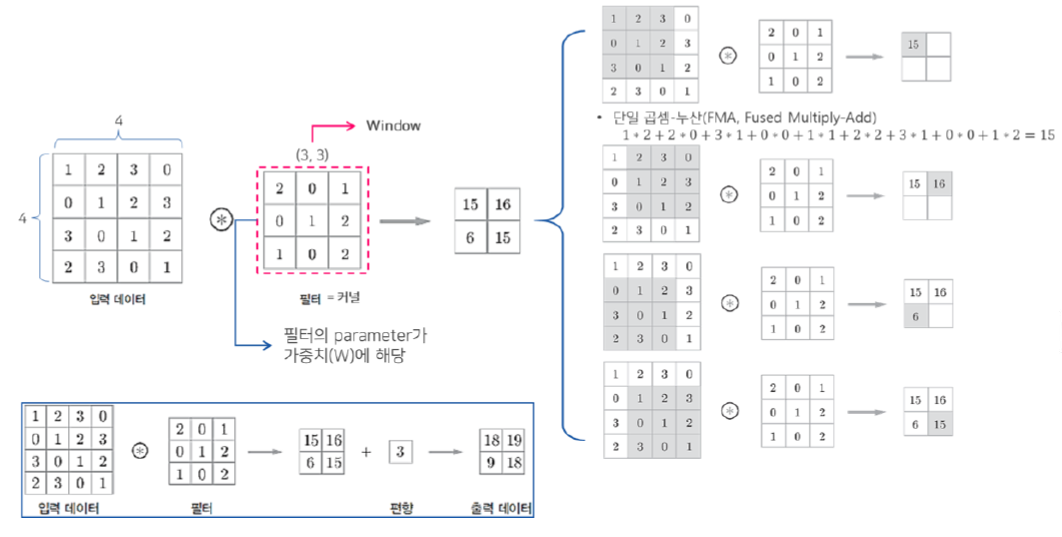
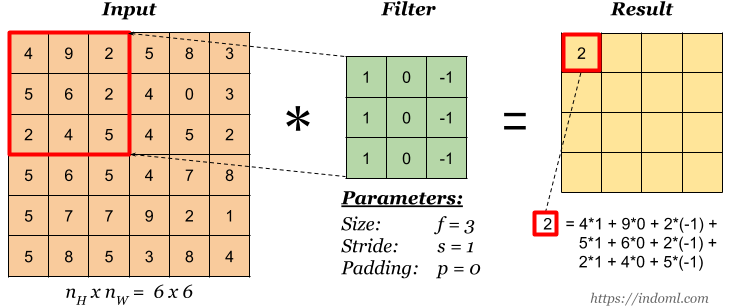
당연합니다. 2차원 convolution의 방법은 아래와 같이 filter(kernel)을 움직이면서 input과 kernel의 공통 부분의 원소들을 곱하여 sum을 구하는 것입니다. 아래 그림을 참고하면 더 이해가 쉬울 것 같네요!
CNN의 구성
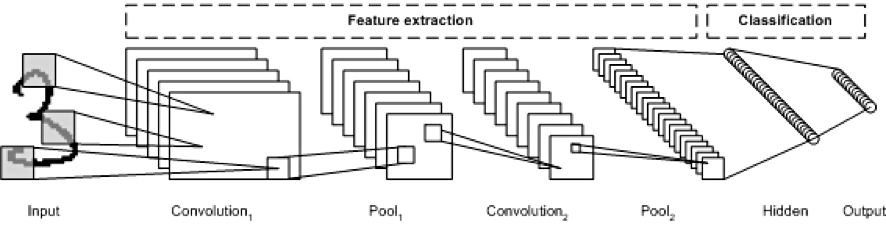
CNN은 다음과 같이 구성됩니다
- 입력 레이어 : 입력 image가 들어오는 layer
- Convolution layer : 입력 이미지의 receptive field에 대하여 convolution 연산을 수행
- Activation layer : Activation 함수를 통과시킵니다 (일반적으로 ReLU함수를 사용합니다)
- Pooling layer : Width와 Height에 대해 downsampling을 수행합니다
- FC layer : 네트워크의 마지막 부분에서 class classfication을 수행합니다
주요 개념 정리
Channel(depth)
이미지 데이터는 주로 R,G,B 3개의 채널로 이루어졌습니다.
Grayscale 이미지 역시 이 R,G,B 값을 이용하여 얻을 수 있으며, 흑백영상은 1채널을 가집니다.
Stride
Stride는 Kernel(filter)가 움직이는 보폭이라고 생각하면 됩니다
stride = 1인 경우 Kernel은 1 pixel씩 움직일 것입니다
stride 값에 따라, convolution 연산의 결과인 Feature map의 크기도 달라집니다
아래 그림은 stride가 1인 경우와 2인 경우일 때입니다. 각각의 output은 4X4, 2X2인 것을 확인할 수 있습니다
Padding
CNN에서는 Kernel 연산과 stride의 영향으로 연산을 하면 할 수록 output의 크기는 작아질 것입니다
이는 Feature의 손실로 이어질 수 있으므로, 부정적인 결과를 초래합니다
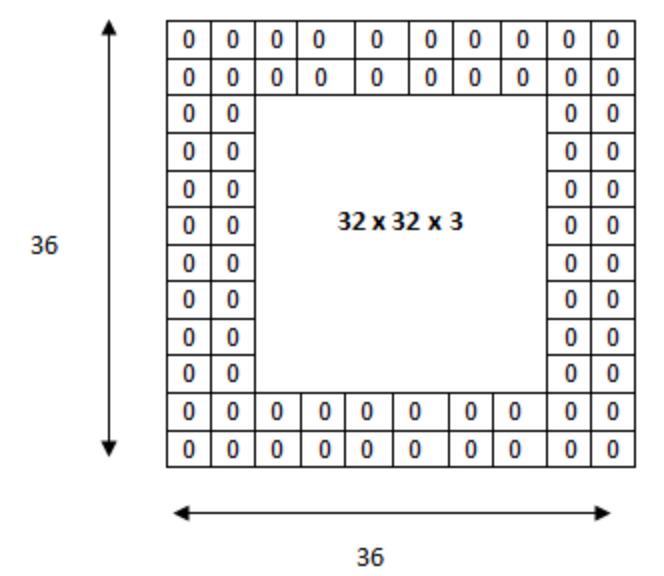
padding은 이를 방지하고자 특정값으로 input의 주변을 채워 넣는 것입니다.
이를 통해서 input과 output의 크기가 같아집니다.
보통 0을 이용하여 input 주변의 값을 채웁니다
Convolution layer
Convolution연산을 통해 결국에 우리는 2차원의 pixel data로부터 Feature(특징) map을 얻을 수 있습니다
그럼 CNN은 이러한 Feature map을 이용하여 결국에 무엇을 학습할까요?
결론부터 말하자면, Kernel의 성분값을 학습하는 것이라고 할 수 있습니다
CNN은 kernel연산을 통해 특징을 추출하므로,
결국에 우리가 어떤 것을 detect하기 위해서는 잘 detect 할 수 있는 Kernel(filter)를 알아야 하겠죠??
Convolution layer에서는 kernel과의 convolution 결과인 Feature map을 반환합니다.
이때, 사용한 kernel의 갯수가 Feature map의 channel(depth)가 됩니다
각 kernel에 대한 결과값(2D)가 kernel의 갯수만큼 있을테니 그렇겠죠?
convolution layer를 통과한 이후에는 Activation layer를 지나면서 activation function을 지난 값이 저장될 것입니다
import tensorflow as tf
class SimpleConvolutionLayer(tf.keras.layers.Layer):
def __init__(self, num_kernels = 32, kernel_size=(3,3), stride = 1):
''' 계층의 초기화
num_kernels : kernel의 갯수
kernel_size : kernel의 크기 (Heigth X Width)
stride : 보폭
'''
super().__init__()
self.num_kernels = num_kernels
self.kernel_size = kernel_size
self.stride = stride
def build(self, input_shape):
'''
input_shape : 계층의 입력 형상(shape). 예를 들어 B X Height X Width X Channel
'''
# input_shape를 BHWC 포맷이라 가정합니다
num_input_channel = input_shape[-1]
kernel_shape = (*self.kernel.size, num_input_channel, self.num_kernels) # 실제 커널 1개의 shape는 (kernel.size X input shape)(3D)이며 이러한 커널이 num_kernels만큼 존재한다
glorot_init = tf.initializers.GlorotUniform() # 필터값을 Glorot 분포를 따르는 값으로 초기화
self.kernels = self.add_weight(name='kernels', shape=kernel_shape, initializer=glorot_init,trainable=True) # 변수를 계층에 추가하기 위한 method
self.bias = self.add_weight(name='bias', shape=(self.num_kernels,), initializer='random_normal',trainable=True) # 편향값 변수에도 동일하게 적용
def call(self, inputs):
'''계층을 호출, 해당 계층의 연산을 입력 텐서에 적용'''
return conv_layer(inputs, self.kernels, self.bias, self.stride)위와 같이 직접 구현할 수도 있지만, Keras API를 이용하여 간단히 model을 instance화 시킬 수 있습니다.
conv = tf.keras.layers.Conv2D(filters=32, kernel_size=(3,3), strides=1, padding='valid', activation='relu')Pooling layer
Pooling layer는 Convolution layer의 출력 데이터 (Activation Map or Feature Map)를 downsampling (크기를 줄이거나 특정 데이터를 강조)하는 역할을 합니다
Pooling의 방법으로는 Max Pooling, Average Pooling, Min Pooling을 주로 이용합니다.
아래 그림처럼 Max pooling은 pool size에서 최댓값을 이용하여 downsampling 하고 있으며, Average Pooling은 평균값을 이용하여 downsampling하고 있습니다

Keras API를 이용하여 인스턴스를 좀 더 간결하게 만들 수 있습니다
avg_pool = tf.keras.layers.AvgPool2D(pool_size=2, strides=2)
max_pool = tf.keras.layers.MaxPool2D(pool_size=2, strides=2)FC layer(Dense layer)
FC layer는 conv-pooling layer의 결과를 이용하여 class를 분류하는 역할을 합니다
먼저 Flatten layer을 통하여 2D image를 1D vector로 만듭니다
이후에 softmax layer를 이용하여 class를 분류합니다

LeNet-5
LeNet은 Yann Lecun이라는 사람이 제시한 초기의 CNN 모델입니다
Input -> Conv1 -> Avg.pooling1 -> Conv2 -> Avg.pooling2 -> Conv3 -> FC1 -> FC2 순서로 모델이 구성됩니다. Architecture detail은 아래와 같습니다.
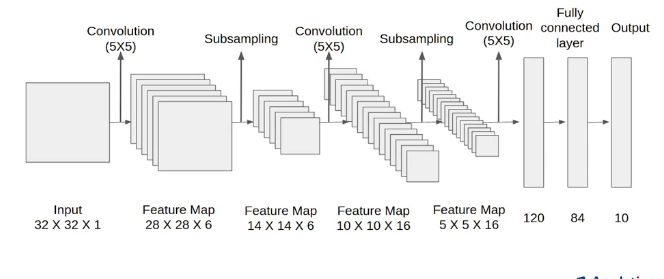
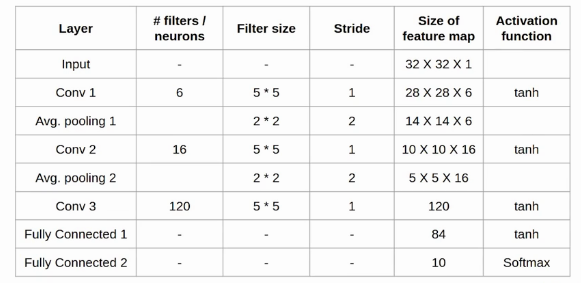
그럼 이제 keras를 이용하여 직접 LeNet-5를 구현해보겠습니다
from tensorflow.keras.models import Model, Sequential
from tensorflow.keras.layers import Conv2D, AveragePooling2D, Flatten, Dense
img_height = 28
img_width = 28
img_channels = 1
input_shape = (img_height, img_width, img_channels)
num_classes = 10 # 0 ~ 9
model = Sequential()
# 1st Block(Conv2D + Avg_pooling)
model.add(Conv2D(6, kernel_size=(5,5), padding='same',
activation='relu',
input_shape=(img_height, img_width, img_channels)))
model.add(AveragePooling2D(pool_size=(2,2)))
# 2nd Block(Conv2D + Avg_pooling)
model.add(Conv2D(6, kernel_size=(5,5), padding='same',
activation='relu',
input_shape=(img_height, img_width, img_channels)))
model.add(AveragePooling2D(pool_size=(2,2)))
# FC layer
model.add(Flatten()) # 2D -> 1D vectors
model.add(Dense(120, activation='relu'))
model.add(Dense(84, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))이제 LeNet-5를 이용하여 MNIST 숫자 데이터를 분류해보겠습니다!
# load data
import tensorflow as tf
import numpy as np
from tensorflow.keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train, X_test = X_train/255.0, X_test/255.0
X_train, X_test = X_train.reshape(-1,*input_shape), X_test.reshape(-1, *input_shape)
# build model
model.compile(optimizer='sgd',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# Callbacks for monitoring
Callbacks = [
# 3 epoch가 지나도 'val_loss'가 개선되지 않으면 훈련을 중단한다
tf.keras.callbacks.EarlyStopping(patience=3, monitor='val_loss')]
# Train
model.fit(X_train, y_train, batch_size=32, epochs=10, validation_data=(X_test,y_test), callbacks=Callbacks)< 실행결과 >
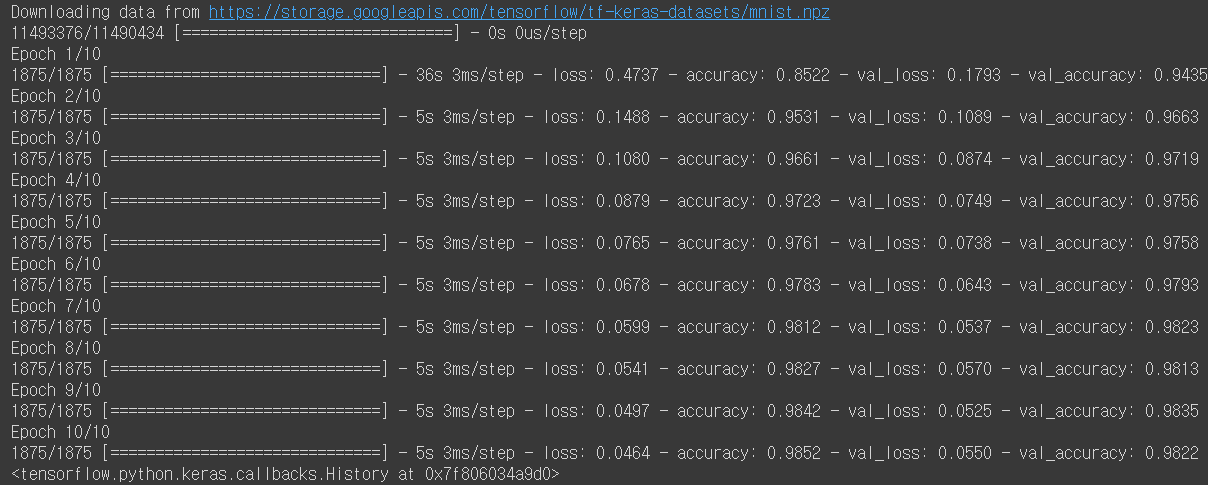
정확도가 chatper1, 2에서 구현했던 것보다 엄청 향상된 것을 볼 수 있습니다!
훈련 프로세스 개선
optimizer
Gradient Descent
GD방법은 앞서 설명하였듯이, 훈련하는 동안 손실 L을 최소화하기 위하여 Gradient값을 backpropagation하여 반복적으로 업데이트 하는 방법입니다.

이 때, learning rate 값을 적절히 설정해 주어야 학습이 잘 될 것입니다.
아래에는 이러한 Gradient Descent 방법의 까다로운 점을 소개하겠습니다.
1) 훈련 속도와 trade-off
만약에 학습률이 너무 높으면 신경망이 빠르게 학습하겠지만, 적절한 최소 Loss값을 찾지 못할 수 있습니다 아래 그림의 (B)를 보면은 update가 좌우로 왔다갔다 하면서 결국 최솟값에는 도달하지 못하고 있습니다
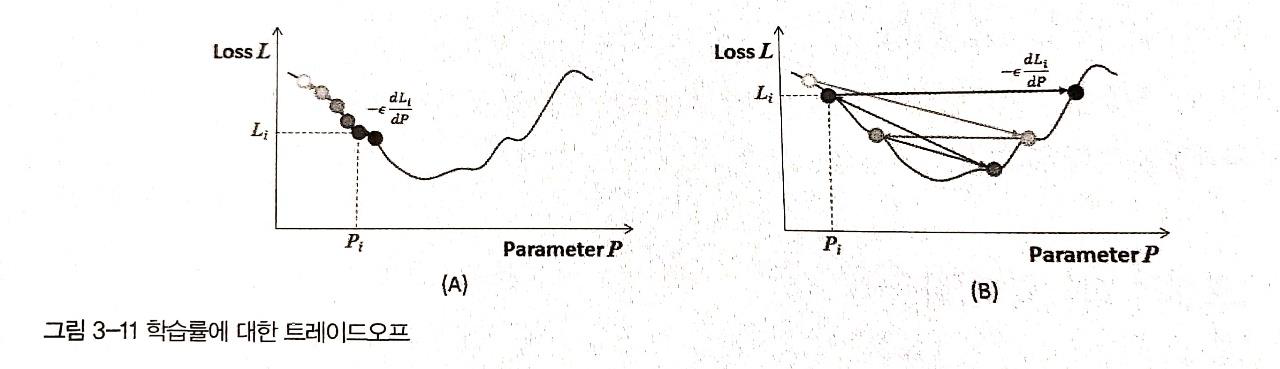
반면에 학습률을 과도하게 낮게 잡으면 수렴하는데 시간이 오래걸린다는 단점이 존재합니다
적절한 학습률을 구하기 위해서 시행착오를 거쳐서 구하는 방법도 있겠지만, 잘 알려진 방법으로는 학습률 감소(learning rate decay)가 있습니다. 이 방법은 epoch가 넘어갈때마다 학습률을 감소시켜서, 처음에는 빨리 학습하지만 점점 속도가 느려지면서, 최솟값을 지나가는 것을 방지하는 효과가 있습니다
2) 준최적 극솟값(Suboptimal local minimum)
이 역시 앞서서 설명드린 개념입니다
non-convex한 loss-function을 이용하면 local minimun에 빠지게 되어 global minimum에 도달하지 못한다는 문제가 발생합니다
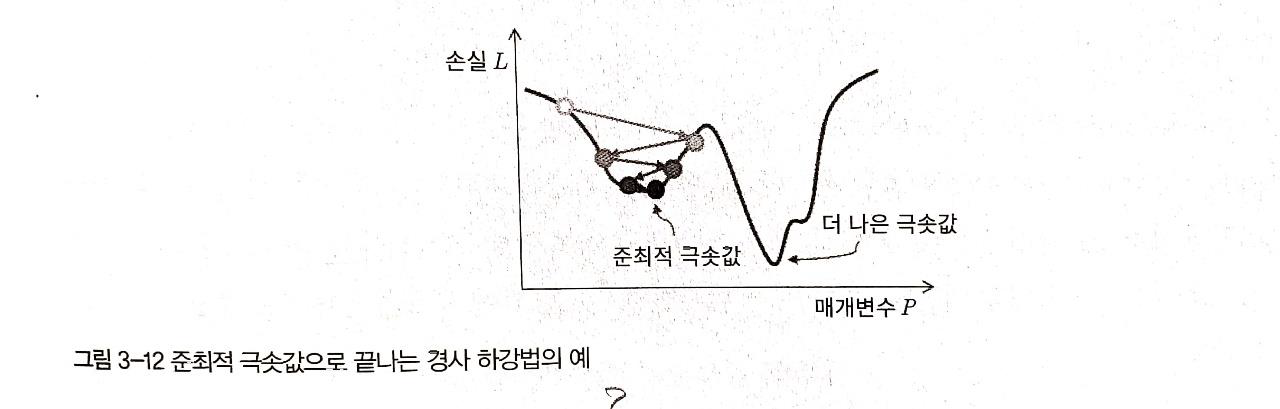
3) 동일한 learning-rate의 적용
전통적인 Gradient Descent 방법에서는 동일한 학습률이 네트워크의 모든 매개변수를 업데이트 하는데 사용됩니다.이러한 방법은 모든 변수가 동일한 민감도를 갖지 않는다는 문제점이 있습니다.
오히려 결정적인 매개변수를 좀 더 신중하게 update하고, 기여도가 떨어지는 매개변수들은 과감하게 update하는 것이 이로울 수 있습니다
고급 최적화 기법
지금부터는 단순한 Gradient Descent 방법을 뛰어넘는, SGD 방법 기반의 고급 최적화 알고리즘들을 소개하겠습니다
Momentum
Momentum(관성)이란 물리학에서 운동상태를 계속 유지하려고자 하는 성질을 뜻합니다.
모멘텀 알고리즘에서는 새로운 변수인 v를 도입하여 update하는데 적용합니다.
v는 방향과 속도를 갖는다고 생각하면 됩니다.
아래 공식에서 보듯이 v는 previous한 v값을 고려하면서, 현재의 gradient 값도 동시에 고려하고 있습니다.
만약에 이전의 v와 현재의 단계가 같은 방향을 나타내면 모멘텀을 더해서 SGD를 그 방향으로 가속화 시킵니다. 반대로 방향이 다르다면 모멘텀은 이전의 v에 방향에 현재의 graident방향을 더한 방향이 됩니다.
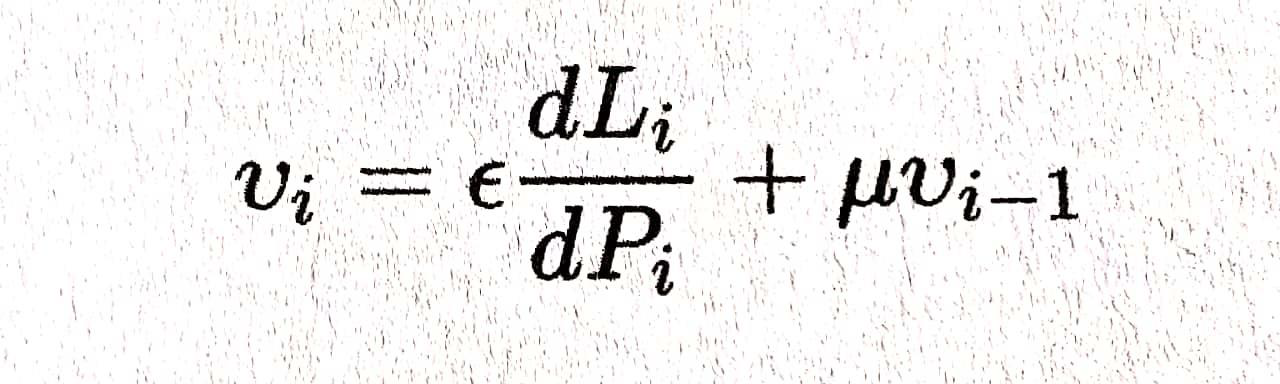
 Keras에서 모멘텀 알고리즘은 optimizer에서 사용할 수 있습니다
Keras에서 모멘텀 알고리즘은 optimizer에서 사용할 수 있습니다
optimizer = tf.optimizers.SGD(learning_rate=0.01, momentum=0.9, decay=0.0, nesterov=False) Nesterov Momentum
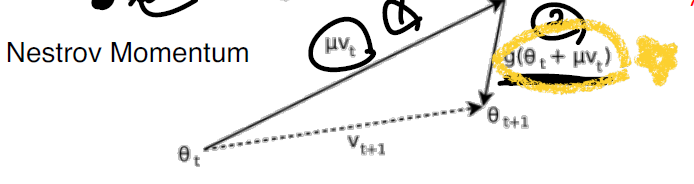
Nesterov 모멘텀은 기존의 모멘텀 방식을 바탕으로 합니다.
기존의 방법과의 차이점으로는
1) 먼저 기존의 v벡터 만큼 먼저 이동한 후,
2) 이동한 곳에서 gradient 벡터값을 계산하고 그만큼 다시 이동합니다.
즉 기존의 방법은 현재 지점에서 기존의 v벡터와 gradient벡터의 합을 구해서 그 합벡터만큼 이동하는 반면에, Nesterov는 먼저 v만큼 이동하고 거기서 grdient벡터를 구해 다시 이동하는 것입니다
Nesterov 방법은 아래와 같이 사용할 수 있습니다
optimizer = tf.optimizers.SGD(learning_rate=0.01, momentum=0.9, decay=0.0, nesterov=True) AdaGrad
AdaGrad 방법은 SGD에서 update를 할 크기(step size)를 정하는 방법입니다
Variable들을 업데이트 할 때, 이전에 많이 움직이지 않았던 변수들을 large step size를 가지는 반면,
이전에 많이 움직였던 변수들은 small step size를 가지게 합니다.
이 방법은 이전에 움직였던 방향으로는 적게, 안움직인 방향으로는 많이 움직이는 방법이 핵심입니다.
Accumulated gradient를 통해 기존까지 움직인 방향을 알 수 있으며, 아래 공식처럼 그것과 역수인 방향으로 update가 일어납니다

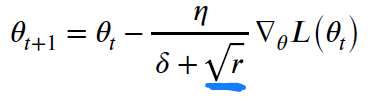
RMSProp
AdaGrad loss function이 convex할 때 잘 작동합니다
하지만 AdaGrad의 문제점으로는 어떤 방향에 대해 large gradient가 있다면은, 이제 그 방향으로는 다시는 update가 되지 않는다는 문제가 발생합니다. 즉 나중에 optimize를 위해 다시 그 방향으로 가야 하는데, 기존에 large gradient가 있었으므로 그 방향으로 갈 수 없다는 문제인 것입니다
RMSProp은 이러한 문제를 해결하고자 exponential moving average를 도입합니다
r(𝑡)= 𝛼(𝑟𝑡−1) + (1 − 𝛼)(∇𝜃𝐿(𝜃𝑡))2
RMSProp의 update 공식은 위와 같습니다. 즉 기존의 r(accumulated gradient)에 𝛼를 곱하고 현재의 gradient제곱에 (1 − 𝛼)를 곱하면서, 점점 update가 되면서 초기에 있던 r값이 가면 갈 수록 줄어들어서, 결국에는 나중에 다시 초기에 있던 방향으로 update가 가능하게 되는 것입니다
Adam
Adam 방법은 실제로 가장 많이 사용하는 방법입니다
이 방법은 Nesetrov Momentum과 RMSProp 방식을 모두 사용합니다
즉 update하는 방향(Nesetrov Momentum)과 update 크기(RMSProp)를 모두 고려하는 방법이라 할 수 있겠습니다

Adam 방법은 bias correction을 같이 해주어야 하는데, 그 이유로는 위의 공식에서 보듯이 초기에 s(1)과 r(1)값이 0으로 빠진다는 문제가 발생하기 때문입니다

Overfitting 피하기
신경망을 효율적으로 가르쳐서 loss를 최소화하는 것으로만은 충분하지 않습니다
신경망은 새로운 이미지에 대해서도 잘 수행할 수 있어야 하는데요, 이를 위해서는 overfitting이 일어나면은 안됩니다
overfitting을 피하기 위한 여러가지 방법에 대해 알아보겠습니다!
조기 중단
overfitting은 작은 훈련 집합에 대해 여러번 반복하면 발생합니다
이를 방지하려면 적절한 훈련 반복 횟수를 알면 될 것입니다
적절한 횟수를 알기 위해서는, 교차 검증(cross-validation)이라는 방법을 사용합니다
즉, 각 epoch이후, 검증 데이터(validation data)를 이용하여 모델의 성능을 측정할 수 있습니다.
이 검증을 통하여, 훈련을 계속해야할지(검증 정확도는 낮지만 증가하는 양상을 보일때), 아니면 훈련을 중단해야할지(검증 정확도가 계속 낮아지는 양상)를 알 수 있습니다. 이 떄, 후자의 경우를 조기 중단이라 부릅니다
L1, L2 규제
overfitting을 방지하는 또 다른 방법으로는 loss-function을 수정하는 방법이 있습니다
가중치에 일정한 규제를 주어서 매개변수의 폭팔적인 증가를 막을 수 있습니다
규제의 방법으로는 L1 norm과 L2 norm를 사용하는 방법이 있습니다.
먼저 L2 norm을 사용하는 Ridge regularization은 신경망의 매개변수의 값의 제곱의 합을 최소화하도록 만듭니다.이를 통해서 매개변수들이 값을 낮게 유지하면서 더 균일하게 분산되는 효과를 볼 수 있습니다
반면에 L1 norm을 사용하는 Lasso regularization은 신경망의 덜 중요한 매개변수를 0으로 축소한다는 효과가 있습니다. 이를 통해 신경망이 노이즈 같은 것을 무시하고 학습한다는 장점이 있습니다
하지만 규제를 과도하게 해버리면 오히려 loss값이 증가합니다.
따라서 적절한 규제를 하는 것이 중요하다고 할 수 있습니다
Keras에서 규제는 아래와 같이 사용할 수 있습니다
# Lasso regularization
l1_reg = tf.keras.regularizers.l1(0.01)
# Ridge regularization
l2_reg = tf.keras.regularizers.l2(0.01)
# 실제 모델에 적용
model = Sequential()
model.add(Conv2D(6, kernel_size=(5,5), padding='same', activation='relu', input_shape=(277,277,3), kernel_regularizer=l1_reg)) Dropout
Dropout은 훈련이 반복될 때마다 타깃 계층의 일부 뉴런들의 연결을 임의로 끊어버리는 방식입니다
따라서 이 방식은 hyperparameter로 끊을 비율( 보통 0.1~0.5 )사이의 값을 취합니다.
dropout을 통하여서 신경망을 임의로 훼손시키면서 견고한 공동의 특징을 학습하게 해주는 모델을 만들 수 있습니다.
예를 들면, dropout을 통해 핵심 특징을 담당하던 뉴런과의 연결이 끊어진 경우, 신경망은 다른 중요한 특징을 알아내려 할 것입니다
Keras에서 예측은 다음과 같이 사용할 수 있습니다
model = Sequential( ..., Dropout(0.2))Batch Normalization
배치 정규화는 이전 계층의 배치 결과를 정규화(평균을 뺀 후 표준편차로 나눔)를 하는 연산입니다
이를 통해 각 매개변수들의 range를 유사화하면서, 기여도를 어느 정도 동일하게 맞출 수 있습니다.
Keras에서는 아래와 같이 사용할 수 있습니다
model.add(Batch_Noramlization())Reference
- 실전! 텐서플로 2를 활용한 딥러닝 컴퓨터비전 chapter03
- 경희대학교 소프트웨어융합학과 로봇센서데이터처리 과목 Lecture slide 16
- http://taewan.kim/post/cnn/
- https://ndb796.tistory.com/477
- https://statinknu.tistory.com/25
