Logistic Regression Classifier 를 공부하기 위해 참고자료를 활용해 작성하였습니다.
데이터 셋 링크: Rain in Australia
참고자료: Logistic Regression Classifier Tutorial
목차
- 로지스틱 회귀 소개
- 로지스틱 회귀 직관
- 로지스틱 회귀의 가정
- 로지스틱 회귀의 유형
- 라이브러리 가져오기
- 데이터셋 가져오기
- 탐색적 데이터 분석
- 특징 벡터 및 대상 변수 선언
- 데이터를 별도의 교육 및 테스트 세트로 분할
- 특성 공학
- 기능 스케일링
- 모델 트레이닝
- 결과 예측
- 정확도 점수 확인
- Confusion matrix
- 분류 지표
- 한계 레벨 조정하기
- ROC - AUC
- k-Fold Cross Validation
- 그리드서치 CV를 이용한 하이퍼파라미터 최적화
- 결과 및 결론
- 참고문헌
1. 로지스틱 회귀 분석 소개
데이터 과학자가 새로운 분류 문제를 접할 때 가장 먼저 떠오르는 알고리즘이 로지스틱 회귀입니다. 로지스틱 회귀는 지도 학습 분류 알고리즘으로, 관측값을 불연속적인 클래스 집합으로 예측하는 데 사용됩니다. 실제로는 관측값을 여러 범주로 분류하는 데 사용됩니다. 따라서 그 출력은 본질적으로 불연속적입니다. 로지스틱 회귀는 로지트 회귀라고도 합니다.(Logistic Regression is also called Logit Regression.) 분류 문제를 해결하는 데 사용되는 가장 간단하고 간단하며 다재다능한 분류 알고리즘 중 하나입니다.
2. Logistic Regression intuition(로지스틱 회귀 직관)
통계학에서 로지스틱 회귀 모델(Logistic Regression model)은 주로 분류 목적으로 널리 사용되는 통계 모델입니다. 즉, 일련의 관측값이 주어지면 로지스틱 회귀 알고리즘을 사용하여 이러한 관측값을 두 개 이상의 불연속적인 클래스로 분류하는 데 도움이 됩니다. 따라서 대상 변수는 본질적으로 이산형입니다.
로지스틱 회귀 알고리즘은 다음과 같이 작동합니다.
Implement linear equation(선형 방정식 구현)
로지스틱 회귀 알고리즘은 독립 변수 또는 설명 변수로 선형 방정식을 구현하여 응답 값을 예측하는 방식으로 작동합니다. 예를 들어, 공부한 시간과 시험 합격 확률을 예로 들어 보겠습니다. 여기서 공부한 시간은 설명 변수이며 x1로 표시됩니다. 시험에 합격할 확률은 응답 또는 목표 변수이며 z로 표시됩니다.
설명 변수(x1)가 하나이고 반응 변수(z)가 하나라면 선형 방정식은 수학적으로 다음과 같은 방정식으로 주어집니다.
z = β0 + β1x1여기서 계수 β0과 β1은 모델의 매개변수입니다.
설명 변수가 여러 개 있는 경우 위의 방정식을 다음과 같이 확장할 수 있습니다.
z = β0 + β1x1 + β2x2 +........ + βnxn여기서 계수 β0, β1, β2 및 βn은 모델의 매개 변수입니다.
따라서 예측된 응답 값은 위의 방정식에 의해 주어지며 z로 표시됩니다.
Sigmoid Function(시그모이드 함수)
z로 표시되는 이 예측된 응답 값은 0과 1 사이의 확률 값으로 변환됩니다. 예측된 값을 확률 값에 매핑하기 위해 시그모이드 함수를 사용합니다. 그런 다음 이 시그모이드 함수는 모든 실제 값을 0과 1 사이의 확률 값으로 매핑합니다.
머신 러닝에서 시그모이드 함수는 예측을 확률에 매핑하는 데 사용됩니다. 시그모이드 함수는 S자 모양의 곡선을 가지고 있습니다. 시그모이드 곡선이라고도 합니다.
시그모이드 함수는 로지스틱 함수의 특수한 경우입니다. 다음 수학 공식으로 표현됩니다.
그래픽으로는 다음 그래프로 시그모이드 함수를 나타낼 수 있습니다.
Sigmoid Function

Decision boundary(결정 경계)
시그모이드 함수는 0과 1 사이의 확률 값을 반환합니다. 이 확률 값은 "0" 또는 "1"인 불연속형 클래스에 매핑됩니다. 이 확률 값을 불연속형 클래스(합격/불합격, 예/아니오, 참/거짓)에 매핑하기 위해 임계값을 선택합니다. 이 임계값(threshold value)을 결정 경계(Decision boundary)라고 합니다. 이 임계값을 초과하면 확률 값을 클래스 1에 매핑하고 그 이하이면 값을 클래스 0에 매핑합니다.
수학적으로 다음과 같이 표현할 수 있습니다.
p ≥ 0.5 => 클래스 = 1
p < 0.5 => 클래스 = 0
일반적으로 의사 결정 경계는 0.5로 설정됩니다. 따라서 확률 값이 0.8(> 0.5)이면 이 관측값을 클래스 1에 매핑합니다. 마찬가지로 확률 값이 0.2(<0.5)인 경우, 이 관측값을 클래스 0에 매핑합니다.
이는 아래 그래프에 표시됩니다.
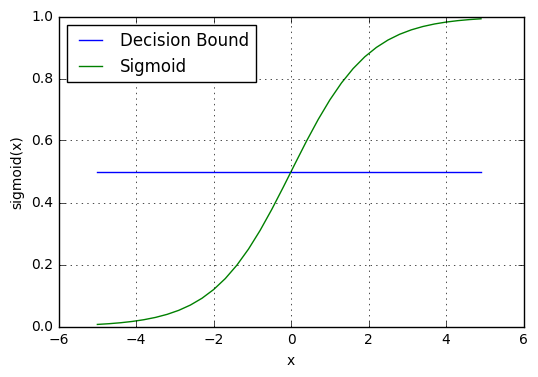
Making predictions(예측하기)
이제 로지스틱 회귀에서 시그모이드 함수와 결정 경계에 대해 알게 되었습니다. 시그모이드 함수와 결정 경계에 대한 지식을 사용하여 예측 함수를 작성할 수 있습니다. 로지스틱 회귀의 예측 함수는 관측값이 양수일 확률, 즉 예 또는 참을 반환합니다. 이를 클래스 1이라고 부르며 P(class = 1)로 표시됩니다. 확률이 1에 가까워지면 관찰이 클래스 1에 속하고, 그렇지 않으면 클래스 0에 속한다고 모델에 대해 더 확신할 수 있습니다.
3. Assumptions of Logistic Regression(로지스틱 회귀의 가정)
로지스틱 회귀 모델에는 몇 가지 주요 가정이 필요합니다. 이러한 가정은 다음과 같습니다.
1. 로지스틱 회귀 모델은 종속 변수가 이진, 다항식 또는 서수여야 합니다.
2. 관측값이 서로 독립적이어야 합니다. 따라서 관측값이 반복된 측정값에서 나온 것이 아니어야 합니다.
3. 로지스틱 회귀 알고리즘은 독립 변수 간에 다중공선성(multicollinearity)이 거의 또는 전혀 필요하지 않습니다. 이는 독립 변수가 서로 너무 높은 상관관계가 없어야 함을 의미합니다.
4. 로지스틱 회귀 모델은 독립 변수의 선형성과 로그 확률을 가정합니다.
5. 로지스틱 회귀 모형의 성공 여부는 표본 크기에 따라 달라집니다. 일반적으로 높은 정확도를 달성하기 위해서는 큰 표본 크기가 필요합니다.4. Types of Logistic Regression(로지스틱 회귀의 유형)
로지스틱 회귀 모델은 대상 변수 범주에 따라 세 가지 그룹으로 분류할 수 있습니다. 이 세 그룹은 다음과 같이 설명됩니다.
1. Binary Logistic Regression(이원 로지스틱 회귀)
이원 로지스틱 회귀에서 대상 변수에는 두 가지 범주가 있습니다. 범주의 일반적인 예로는 예 또는 아니오, 좋음 또는 나쁨, 참 또는 거짓, 스팸 또는 스팸 없음, 합격 또는 불합격이 있습니다.
2. Multinomial Logistic Regression(다항 로지스틱 회귀)
다항 로지스틱 회귀에서 대상 변수는 특정 순서가 아닌 세 개 이상의 범주를 갖습니다. 따라서 세 개 이상의 명목 범주가 있습니다. 예를 들어 사과, 망고, 오렌지, 바나나 등 과일 카테고리의 유형이 있습니다.
3. Ordinal Logistic Regression(서수 로지스틱 회귀)
서수 로지스틱 회귀에서는 대상 변수에 세 개 이상의 서수 범주가 있습니다. 따라서 범주에는 내재적 순서가 있습니다. 예를 들어, 학생의 성적을 나쁨, 보통, 좋음, 우수로 분류할 수 있습니다.
5. Import libraries(라이브러리 가져오기)
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib.pyplot as plt # data visualization
import seaborn as sns # statistical data visualization6. Import dataset(데이터 세트 가져오기)
7. Exploratory data analysis(탐색적 데이터 분석)
이제 데이터를 탐색하여 데이터에 대한 인사이트를 얻겠습니다.
Types of variables(변수 유형)
이 섹션에서는 데이터 집합을 범주형 변수와 숫자형 변수로 구분합니다. 데이터 집합에는 범주형 변수와 숫자형 변수가 혼합되어 있습니다. 범주형 변수는 데이터 유형 객체를 갖습니다. 숫자 변수는 데이터 유형이 float64입니다.
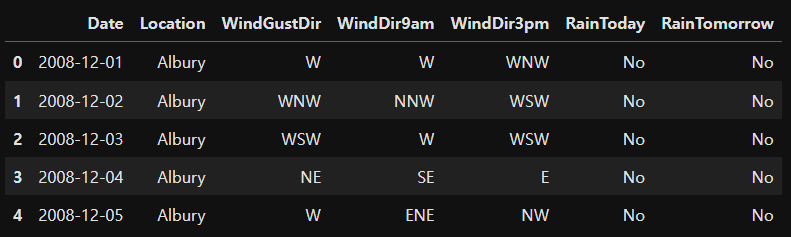
우선 범주형 변수를 찾아보겠습니다.
범주형 변수는 다음과 같습니다. : ['Date', 'Location', 'WindGustDir', 'WindDir9am', 'WindDir3pm', 'RainToday', 'RainTomorrow']
Summary of categorical variables(범주형 변수 요약)
-
날짜 변수가 있습니다. Date 열로 표시됩니다.
-
범주형 변수는 6가지가 있습니다. Location, WindGustDir, WindDir9am, WindDir3pm, RainToday 및 RainTomorrow가 그것입니다.
-
이진 범주형 변수는 RainToday와 RainTomorrow 두 가지가 있습니다.
-
대상 변수는 RainTomorrow입니다.
Explore problems within categorical variables(범주형 변수 내에서 문제 탐색)
먼저 범주형 변수를 살펴보겠습니다.
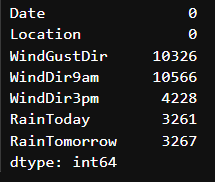
Missing values in categorical variables(범주형 변수의 누락된 값)
데이터 집합에 결측값이 포함된 범주형 변수가 4개만 있음을 알 수 있습니다. WindGustDir, WindDir9am, WindDir3pm, RainToday가 그것입니다.
Frequency counts of categorical variables(범주형 변수의 빈도 수)
이제 범주형 변수의 빈도수를 확인해 보겠습니다.
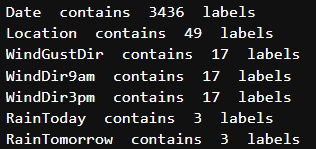
Number of labels: cardinality(레이블 수: 카디널리티)
범주형 변수 내의 레이블 수를 카디널리티라고 합니다. 변수 내의 레이블 수가 많으면 높은 카디널리티라고 합니다. 높은 카디널리티는 머신 러닝 모델에서 몇 가지 심각한 문제를 일으킬 수 있습니다. 따라서 높은 카디널리티를 확인해 보겠습니다.
전처리해야 하는 Date 변수가 있음을 알 수 있습니다. 다음 섹션에서 전처리를 수행하겠습니다.
다른 모든 변수는 상대적으로 적은 수의 변수를 포함하고 있습니다.
Feature Engineering of Date Variable(날짜 변수의 기능 엔지니어링)
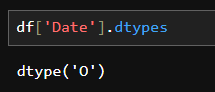
DataFrame의 컨텍스트에서 보는 것은 dtype('O')일반적으로 열에 동종 숫자 또는 범주형 데이터 유형이 아닌 문자열, 목록 또는 기타 Python 개체가 될 수 있는 이기종 데이터 유형이 포함되어 있음을 나타냅니다.
Date 변수의 데이터 유형이 객체임을 알 수 있습니다. 현재 객체로 코딩된 날짜를 날짜/시간 형식으로 파싱하겠습니다.
Date 변수에서 세 개의 열이 추가로 생성된 것을 볼 수 있습니다. 이제 데이터 집합에서 원래 Date 변수를 삭제하겠습니다.
이제 데이터 집합에서 Date 변수가 제거된 것을 볼 수 있습니다.
Explore Categorical Variables(범주형 변수 살펴보기)
이제 범주형 변수를 하나씩 살펴보겠습니다.
Explore Numerical Variables(숫자 변수 살펴보기)
숫자형 변수는 다음과 같습니다. : ['MinTemp', 'MaxTemp', 'Rainfall', 'Evaporation', 'Sunshine', 'WindGustSpeed', 'WindSpeed9am', 'WindSpeed3pm', 'Humidity9am', 'Humidity3pm', 'Pressure9am', 'Pressure3pm', 'Cloud9am', 'Cloud3pm', 'Temp9am', 'Temp3pm', 'Year', 'Month', 'Day']
Summary of numerical variables
-
16개의 숫자 변수가 있습니다.
-
These are given by
MinTemp,MaxTemp,Rainfall,Evaporation,Sunshine,WindGustSpeed,WindSpeed9am,WindSpeed3pm,Humidity9am,Humidity3pm,Pressure9am,Pressure3pm,Cloud9am,Cloud3pm,Temp9amandTemp3pm. -
모든 숫자 변수는 연속형입니다.
Explore problems within numerical variables(숫자 변수 내에서 문제 탐색하기)
이제 숫자 변수를 살펴보겠습니다.
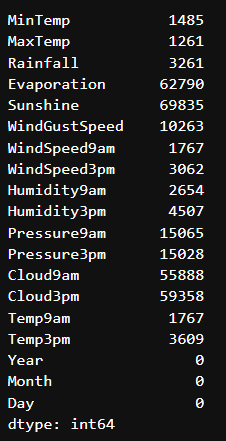
Missing values in numerical variables(숫자 변수의 누락된 값)
16개의 숫자 변수에 모두 결측값이 포함되어 있음을 알 수 있습니다.
Outliers in numerical variables(숫자 변수의 이상값)
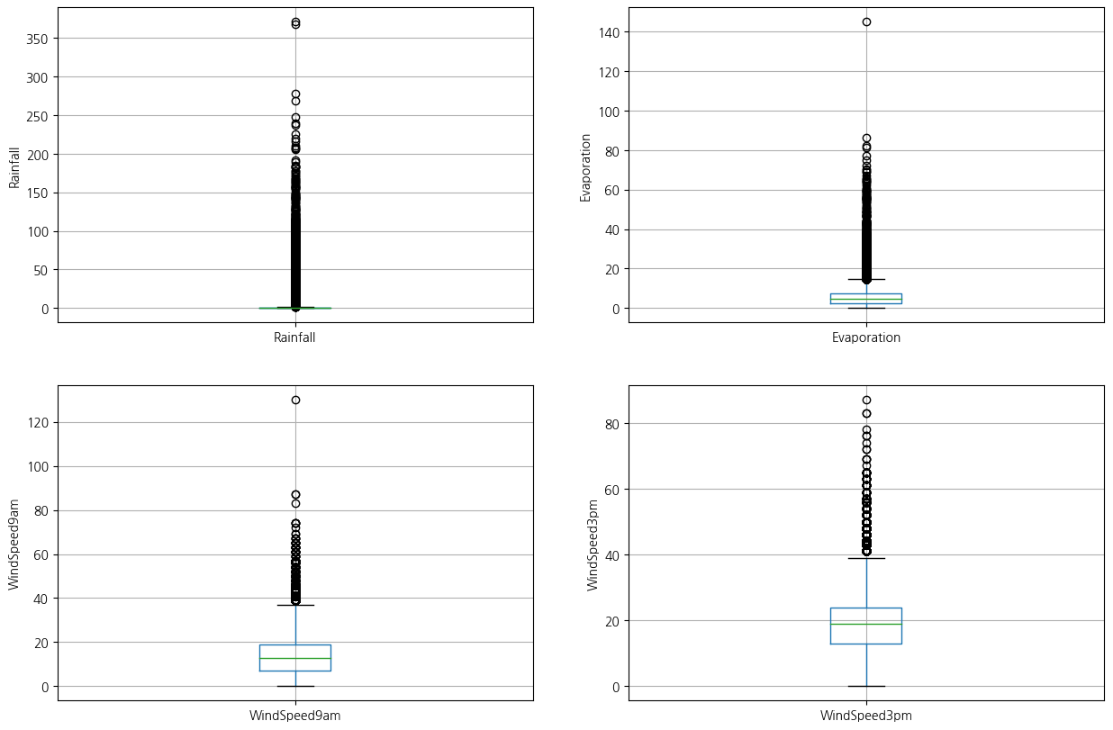
자세히 살펴보면 Rainfall, Evaporation, WindSpeed9am 및 WindSpeed3pm 열에 이상값이 포함될 수 있음을 알 수 있습니다.
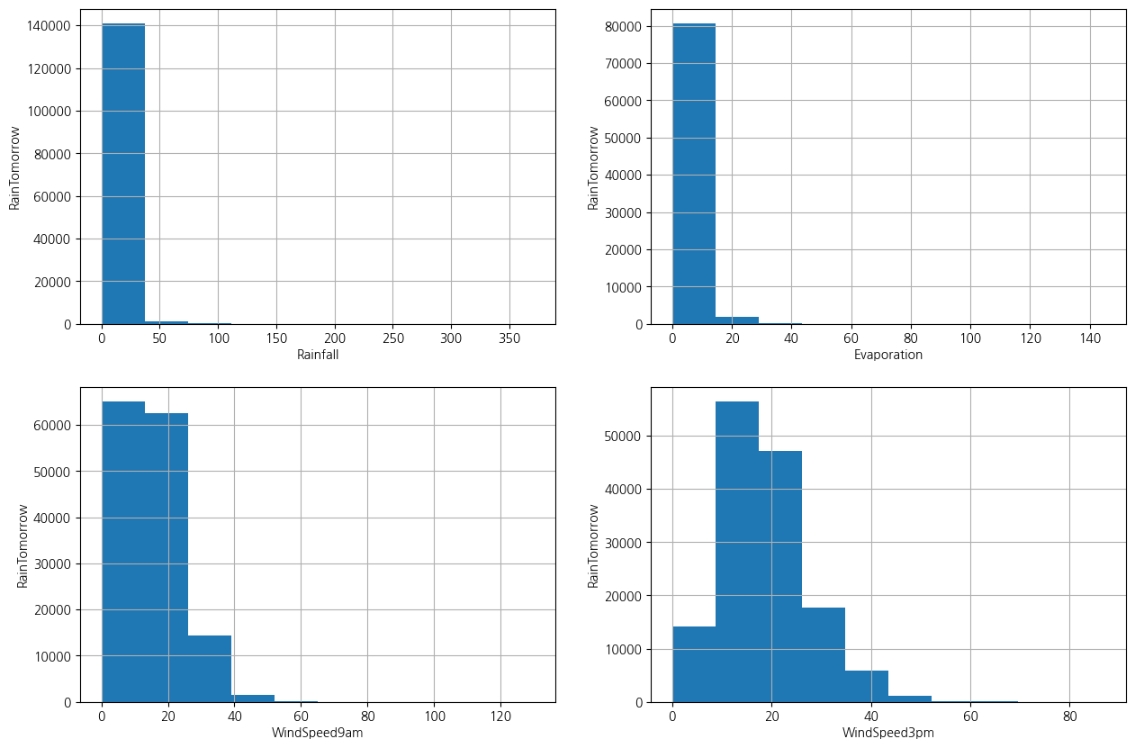
위 변수의 이상값을 시각화하기 위해 박스 플롯을 그려보겠습니다.
위의 박스 플롯을 보면 이러한 변수에 많은 이상값이 있음을 확인할 수 있습니다.
Check the distribution of variables(변수 분포 확인)
이제 히스토그램을 그려서 분포를 확인하여 정상 분포인지 왜곡된 분포인지 확인하겠습니다. 변수가 정규 분포를 따르는 경우 극값 분석을 수행하고, 왜곡된 경우 IQR(사분위수 범위)을 찾습니다.
네 가지 변수가 모두 왜곡되어 있음을 알 수 있습니다. 따라서 사분위수 간 범위를 사용하여 이상값을 찾겠습니다.
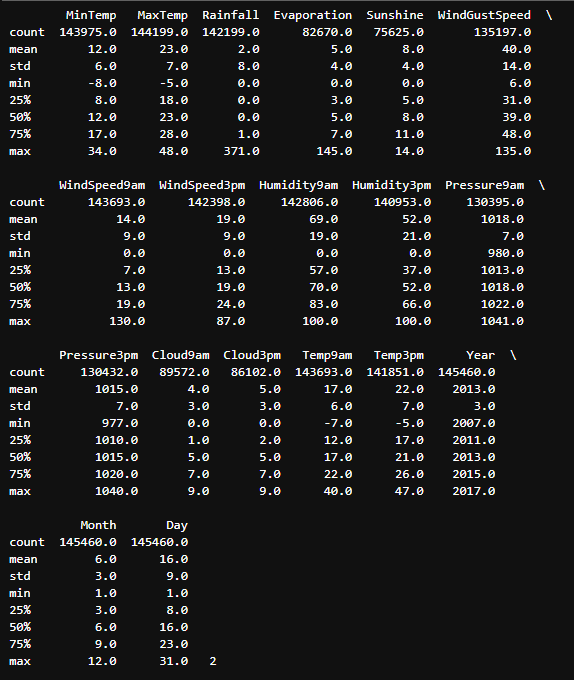
Rainfall의 경우 최소값과 최대값은 0.0과 371.0입니다. 따라서 이상값은 3.2를 초과하는 값입니다.
Evaporation의 경우 최소값과 최대값은 0.0과 145.0입니다. 따라서 이상값은 21.8을 초과하는 값입니다.
WindSpeed9am의 경우 최소값과 최대값은 0.0과 130.0입니다. 따라서 이상값은 55.0을 초과하는 값입니다.
WindSpeed3pm의 경우 최소값과 최대값은 0.0과 87.0입니다. 따라서 이상값은 57.0을 초과하는 값입니다.
8. Declare feature vector and target variable(특징 벡터 및 대상 변수 선언)
9. Split data into separate training and test set(데이터를 별도의 학습 및 테스트 집합으로 분할)
10. Feature Engineering(기능 엔지니어링)
Feature Engineering은 원시 데이터를 유용한 피처로 변환하여 모델을 더 잘 이해하고 예측력을 높이는 데 도움이 되는 프로세스입니다. 다양한 유형의 변수에 대해 피처 엔지니어링을 수행합니다.
먼저 범주형 변수와 숫자형 변수를 다시 구분하여 표시해 보겠습니다.
결측률입니다.
가정
데이터가 완전히 무작위로 누락되었다고 가정합니다(MCAR). 결측값을 추정하는 데 사용할 수 있는 두 가지 방법이 있습니다. 하나는 평균 또는 중앙값 추정이고 다른 하나는 무작위 샘플 추정입니다. 데이터 집합에 이상값이 있는 경우 중앙값 보정을 사용해야 합니다. 중앙값 대입이 이상값에 강하기 때문에 중앙값 대입을 사용하겠습니다.
데이터의 적절한 통계적 측정값(이 경우 중앙값)을 사용하여 결측치를 추정합니다. 추정은 훈련 집합에 대해 수행한 다음 테스트 집합으로 전파해야 합니다. 즉, 훈련 세트와 테스트 세트 모두에서 결측치를 채우는 데 사용할 통계적 측정값은 훈련 세트에서만 추출해야 합니다. 이는 과적합을 피하기 위한 것입니다.
X_train 및 X_test의 누락된 값을 X_train의 각 열 중앙값으로 대치
Engineering missing values in categorical variables(범주형 변수의 엔지니어링 결측치)
누락된 범주형 변수를 가장 빈번한 값으로 대치
X_train과 X_test에 누락된 값이 없음을 알 수 있습니다.
Engineering outliers in numerical variables(숫자 변수의 엔지니어링 이상값)
Rainfall, Evaporation, WindSpeed9am 및 WindSpeed3pm 열에 이상값이 포함되어 있음을 확인했습니다. 위 변수에서 최대값을 제한하고 이상값을 제거하기 위해 탑 코딩 방식을 사용하겠습니다.
이제 Rainfall, Evaporation, WindSpeed9am 및 WindSpeed3pm 열의 이상값이 상한선을 넘은 것을 볼 수 있습니다.
Encode categorical variables(범주형 변수 인코딩)
이제 모델 구축을 위한 훈련 및 테스트가 준비되었습니다. 그 전에 모든 특징 변수를 동일한 척도로 매핑해야 합니다. 이를 피처 스케일링이라고 합니다. 다음과 같이 하겠습니다.
11. Feature Scaling(기능 확장)
12. Model training(모델 교육)
13. Predict results(결과 예측)
predictproba method(예측프로바 메서드)
예측_프로바 메서드는 이 경우 대상 변수(0과 1)에 대한 확률을 배열 형식으로 제공합니다.
0은 비가 오지 않을 확률, 1은 비가 올 확률을 나타냅니다.
14. Check accuracy score(정확도 점수 확인)
여기서 y_test는 실제 클래스 레이블이고 y_pred_test는 테스트 집합에서 예측된 클래스 레이블입니다.
Compare the train-set and test-set accuracy(훈련 세트와 테스트 세트의 정확도 비교하기)
이제 훈련 세트와 테스트 세트의 정확도를 비교하여 과적합(overfitting) 여부를 확인하겠습니다.
- 훈련 세트 정확도 점수 : 0.8488
Check for overfitting and underfitting(과적합과 과소적합 여부 확인)
- Training set score: 0.8488
- Test set score: 0.8484
훈련 세트 정확도 점수는 0.8488이고 테스트 세트 정확도는 0.8484입니다. 이 두 값은 꽤 비슷합니다. 따라서 과적합 문제는 없습니다.
로지스틱 회귀에서는 기본값인 C = 1을 사용합니다. 이 값은 훈련과 테스트 집합 모두에서 약 85%의 정확도로 우수한 성능을 제공합니다. 그러나 훈련과 테스트 집합 모두에서 모델 성능은 매우 비슷합니다. 이는 과소 적합의 경우일 가능성이 높습니다.
C를 늘려서 더 유연한 모델을 맞춰 보겠습니다.
로지스틱 회귀에서 정규화 항은 하이퍼파라미터에 의해 제어됩니다 C. 매개 C변수는 로지스틱 회귀 모델에서 정규화의 강도를 결정합니다. 정규화 강도의 역수입니다. 즉, 값이 작을수록 C정규화가 더 강해지고 값이 클수록 C정규화의 양이 줄어듭니다.
정규화는 기계 학습 모델에서 과적합을 방지하는 데 사용되는 기술입니다. 과적합은 모델이 학습 데이터에 대해 잘 수행되지만 보이지 않는 데이터(예: 테스트 세트)에 대해 일반화하지 못하는 경우에 발생합니다. 정규화는 모델의 복잡성을 제어하는 데 도움을 주어 모델을 더욱 강력하게 만들고 일반화 성능을 향상시킵니다.
가 작을 때 C(강력한 정규화) 로지스틱 회귀 모델은 극단적인 매개변수 값을 피하면서 더 간단하고 매끄러운 결정 경계로 데이터를 맞추려고 합니다. 이는 과적합을 방지하는 데 도움이 될 수 있습니다. 반면에 가 C크면(약한 정규화) 모델이 더 유연해져서 데이터에 더 가깝게 맞출 수 있고 특히 데이터 세트가 작거나 잡음이 많은 경우 잠재적으로 과적합이 발생할 수 있습니다.
Cscikit-learn의 기본값은 LogisticRegression1.0이며, 이는 보통 정규화가 기본적으로 적용됨을 의미합니다. 의 값을 늘리면 C정규화의 양이 줄어들어 모델이 더 유연해지고 잠재적으로 훈련 세트에서 더 나은 성능을 얻을 수 있습니다. 그러나 매우 큰 값으로 설정할 때는 C모델이 데이터의 노이즈에 너무 민감해 과적합될 수 있으므로 주의해야 합니다.
매개변수를 조정할 때 C교차 검증과 같은 기술을 사용하여 보이지 않는 데이터로 잘 일반화되는 최적의 값을 찾는 것이 필수적입니다. 이를 통해 과대적합과 과소적합 간의 올바른 균형을 유지하고 새 데이터에서 최상의 성능을 얻을 수 있습니다. 의 선택은 C특정 데이터 세트와 당면한 문제에 따라 다르므로 특정 사례에 가장 적합한 값을 찾기 위해 다양한 값을 실험해 보는 것이 좋습니다.
C=100으로 로지스틱 회귀 모델에 적합
- Training set score: 0.8489
- Test set score: 0.8492
C=100이 테스트 세트 정확도를 높이고 훈련 세트 정확도도 약간 증가한다는 것을 알 수 있습니다. 따라서 더 복잡한 모델일수록 성능이 더 좋다는 결론을 내릴 수 있습니다.
이제 C=0.01을 설정하여 기본값인 C=1보다 더 정규화된 모델을 사용하면 어떻게 되는지 살펴보겠습니다.
- Training set score: 0.8427
- Test set score: 0.8418
따라서 C=0.01을 설정하여 보다 정규화된 모델을 사용하면 학습 및 테스트 세트 정확도가 모두 기본 매개변수에 비해 감소합니다.
Compare model accuracy with null accuracy(모델 정확도와 널 정확도 비교)
따라서 모델 정확도는 0.8484입니다. 하지만 위의 정확도만으로는 모델이 매우 우수하다고 말할 수 없습니다. 널 정확도와 비교해야 합니다. 널 정확도는 항상 가장 빈번한 클래스를 예측하여 얻을 수 있는 정확도입니다.
따라서 먼저 테스트 세트의 클래스 분포를 확인해야 합니다.
가장 빈번한 클래스의 발생 횟수가 22726회임을 알 수 있습니다. 따라서 22726을 총 발생 횟수로 나누면 널 정확도를 계산할 수 있습니다.
모델 정확도 점수는 0.8489이지만 널 정확도 점수는 0.7812임을 알 수 있습니다. 따라서 로지스틱 회귀 모델이 클래스 레이블을 예측하는 데 매우 효과적이라는 결론을 내릴 수 있습니다.
이제 위의 분석을 바탕으로 분류 모델의 정확도가 매우 우수하다는 결론을 내릴 수 있습니다. 우리 모델은 클래스 레이블을 예측하는 측면에서 매우 잘 작동하고 있습니다.
하지만 값의 기본 분포는 제공하지 않습니다. 또한 분류기가 어떤 유형의 오류를 범하고 있는지에 대해서도 알려주지 않습니다.
혼동 행렬이라는 또 다른 도구가 우리를 구해줍니다.
15. Confusion matrix(혼동 매트릭스)
혼동 행렬은 분류 알고리즘의 성능을 요약하는 도구입니다. 혼동 행렬을 통해 분류 모델의 성능과 모델에서 발생하는 오류 유형을 명확하게 파악할 수 있습니다. 혼동 행렬은 각 범주별로 분류된 올바른 예측과 잘못된 예측에 대한 요약을 제공합니다. 요약은 표 형식으로 표시됩니다.
분류 모델 성능을 평가하는 동안 네 가지 유형의 결과가 나올 수 있습니다. 이 네 가지 결과는 다음과 같습니다.
True Positives (TP) - TP은 관찰이 특정 클래스에 속할 것으로 예측하고 관찰이 실제로 해당 클래스에 속할 때 발생합니다.
True Negatives (TN) - TN은 관찰이 특정 클래스에 속하지 않는다고 예측했지만 실제로 관찰이 해당 클래스에 속하지 않을 때 발생합니다.
False Positives (FP) - FP은 관찰이 특정 클래스에 속한다고 예측했지만 실제로는 해당 클래스에 속하지 않을 때 발생합니다. 이러한 유형의 오류를 유형 I 오류라고 합니다.
False Negatives (FN) - FN은 관측이 특정 클래스에 속하지 않는다고 예측했지만 실제로는 해당 클래스에 속할 때 발생합니다. 이는 매우 심각한 오류이며 유형 II 오류라고 합니다.
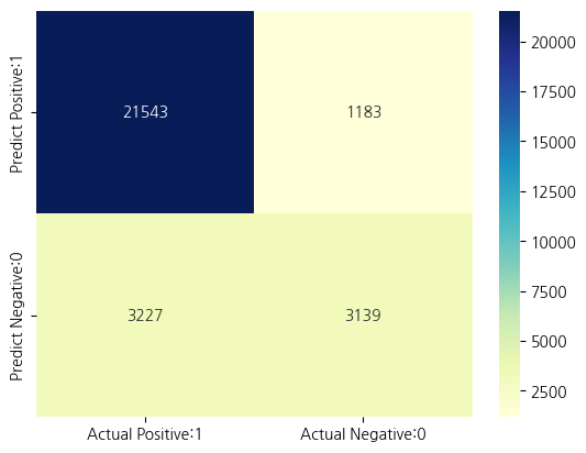
이 네 가지 결과는 아래에 제시된 혼동 행렬에 요약되어 있습니다.
-
True Positives(실제 양성:1 및 예측 양성:1) - 21543 -
True Negatives(실제 음성:0 및 예측 음성:0) - 3139 -
False Positives(실제 음성:0, 양성 예측:1) - 1183(유형 I 오류) -
False Negatives(실제 양성:1, 예측 음성:0) - 3227(유형 II 오류)
16. Classification metrices(분류 메트릭)
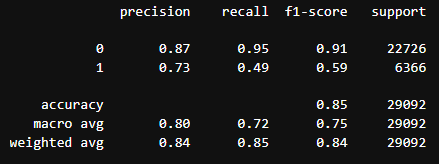
Classification Report(분류 보고서)
분류 보고서는 분류 모델 성능을 평가하는 또 다른 방법입니다. 여기에는 모델의 정확도, 재검색, F1 및 지원 점수가 표시됩니다. 이러한 용어는 나중에 설명하겠습니다.
다음과 같이 분류 보고서를 인쇄할 수 있습니다.
Classification accuracy(분류 정확도)
classification_accuracy = (TP + TN) / float(TP + TN + FP + FN)
Classification accuracy : 0.8484
Classification error(분류 오류)
classification_error = (FP + FN) / float(TP + TN + FP + FN)
Classification error : 0.1516
Precision(정확도)
정확도는 예측된 모든 양성 결과 중 올바르게 예측된 양성 결과의 비율로 정의할 수 있습니다. 정확도는 오탐과 미탐의 합계(TP + FP)에 대한 정탐(TP)의 비율로 나타낼 수 있습니다.
따라서 정밀도는 정확하게 예측된 긍정적인 결과의 비율을 식별합니다. 부정 클래스보다 긍정 클래스에 더 관심이 있습니다.
수학적으로 정밀도는 TP와 (TP + FP)의 비율로 정의할 수 있습니다.
Precision : 정확하게 예측한값. positive로 예측한 값중에 True인 비율을 말한다. TP to (TP + FP).
precision = TP / float(TP + FP)
Precision : 0.9479
Recall = Sensitivity(리콜)
리콜은 실제 양성 결과 중 올바르게 예측된 양성 결과의 비율로 정의할 수 있습니다. 이는 정탐(TP)과 오탐(TP + FN)의 합에 대한 정탐(TP)의 비율로 나타낼 수 있습니다. 리콜은 민감도라고도 합니다.
리콜은 정확하게 예측된 실제 양성 결과의 비율을 나타냅니다.
수학적으로 회상률은 TP와 (TP + FN)의 비율로 나타낼 수 있습니다.
recall : 모든 positive 중 True positive 로 정확히 예측한 비율 TP to (TP + FN).
recall = TP / float(TP + FN)
Recall or Sensitivity : 0.8697
True Positive Rate(진양성률)
진양성률은 리콜과 동의어입니다.
true_positive_rate = TP / float(TP + FN)
True Positive Rate : 0.8697
False Positive Rate(위양성 비율)
실제 음성들중에 양성으로 예측된 비율(negative 를 틀린 비율)
false positive / false positive + true negative
-
True Negatives(실제 음성:0 및 예측 음성:0) - 3139 -
False Positives(실제 음성:0, 양성 예측:1) - 1183(유형 I 오류)
false_positive_rate = FP / float(FP + TN)
False Positive Rate : 0.2737
Specificity(특이성)
실제 음성들중에 음성으로 예측된 비율(negative 를 맟춘 비율)
True Negatives / (True Negatives + False Positives)
-
True Negatives(실제 음성:0 및 예측 음성:0) - 3139 -
False Positives(실제 음성:0, 양성 예측:1) - 1183(유형 I 오류)
specificity = TN / (TN + FP)
Specificity : 0.7263
f1-score
f1-score는 정확도와 회수율 (precision and recall)의 가중치 조화 평균입니다. f1-score는 정확도와 회수율(precision and recall)의 조화 평균으로, 최고값은 1.0이고 최저값은 0.0입니다. 따라서 f1-score는 정확도와 재인용률(precision and recall)을 계산에 포함하므로 정확도 측정값보다 항상 낮습니다. 분류기 모델을 비교할 때는 글로벌 정확도가 아닌 f1-score의 가중 평균을 사용해야 합니다.
Support(지원)
지원은 데이터 세트에서 클래스의 실제 발생 횟수입니다.
17. Adjusting the threshold level(임계값 레벨 조정하기)
Observations
-
각 행에서 숫자의 합계는 1입니다.
-
0과 1의 두 클래스에 해당하는 2개의 열이 있습니다.
-
클래스 0 - 내일 비가 내리지 않을 것으로 예상되는 확률입니다.
-
클래스 1 - 내일 비가 올 것으로 예상되는 확률입니다.
-
-
예측 확률의 중요성
- 비가 올 확률 또는 비가 오지 않을 확률에 따라 관측값의 순위를 매길 수 있습니다.
-
예측_프로바 프로세스
-
확률을 예측합니다.
-
가장 높은 확률을 가진 클래스를 선택합니다.
-
-
분류 임계값 수준
-
분류 임계값 수준은 0.5입니다.
-
클래스 1 - 확률이 0.5를 초과하면 비가 내릴 것으로 예측됩니다.
-
클래스 0 - 확률이 0.5 미만인 경우 비가 내리지 않을 확률이 예측됩니다.
-
Observations
-
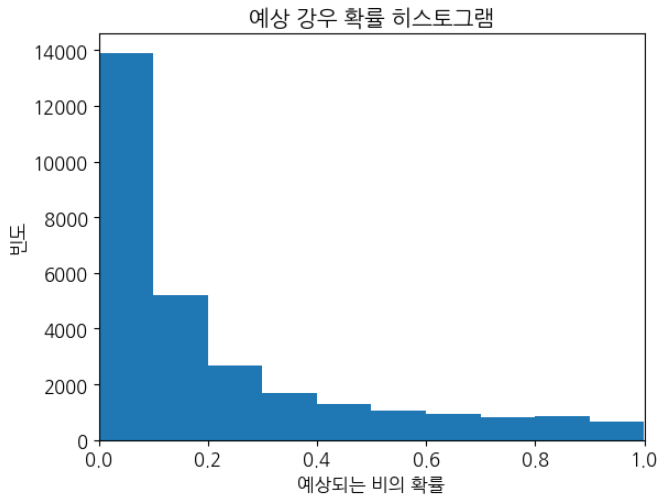
위의 히스토그램이 매우 양으로 치우쳐 있음을 알 수 있습니다.
-
첫 번째 열은 0.0에서 0.1 사이의 확률로 약 14,000개의 관측값이 있음을 알려줍니다.
-
확률이 0.5를 초과하는 소수의 관측값이 있습니다.
-
따라서 이 적은 수의 관측으로 내일 비가 올 것이라고 예측할 수 있습니다.
-
대부분의 관측은 내일 비가 내리지 않을 것으로 예측합니다.
Lower the threshold(임계값 낮추기)
With 0.1 threshold the Confusion Matrix is
[[13291 9435][ 571 5795]]
with 19086 correct predictions,
9435 Type I errors( False Positives),
571 Type II errors( False Negatives),
Accuracy score: 0.6560566478757046
Sensitivity: 0.9103047439522463
Specificity: 0.5848367508580481
====================================================
With 0.2 threshold the Confusion Matrix is
[[17742 4984][ 1365 5001]]
with 22743 correct predictions,
4984 Type I errors( False Positives),
1365 Type II errors( False Negatives),
Accuracy score: 0.7817613089509143
Sensitivity: 0.7855796418473139
Specificity: 0.7806917187362492
====================================================
With 0.3 threshold the Confusion Matrix is
[[19744 2982][ 2043 4323]]
with 24067 correct predictions,
2982 Type I errors( False Positives),
2043 Type II errors( False Negatives),
Accuracy score: 0.8272721022961639
Sensitivity: 0.679076343072573
Specificity: 0.8687846519405087
====================================================
With 0.4 threshold the Confusion Matrix is
[[20840 1886][ 2646 3720]]
with 24560 correct predictions,
1886 Type I errors( False Positives),
2646 Type II errors( False Negatives),
Accuracy score: 0.844218341812182
Sensitivity: 0.58435438265787
Specificity: 0.9170113526357476
====================================================
Comments
- 이진법 문제에서는 예측 확률을 클래스 예측으로 변환하기 위해 기본적으로 임계값 0.5가 사용됩니다.
- 임계값을 조정하여 민감도 또는 특이도를 높일 수 있습니다.
- 민감도와 특이도는(Sensitivity and specificity) 반비례 관계입니다. 하나를 늘리면 항상 다른 하나가 줄어들고 그 반대도 마찬가지입니다.
- 임계값을 높이면 정확도가 높아지는 것을 볼 수 있습니다.
- 임계값 수준을 조정하는 것은 모델 작성 프로세스에서 수행하는 마지막 단계 중 하나여야 합니다.
18. ROC - AUC
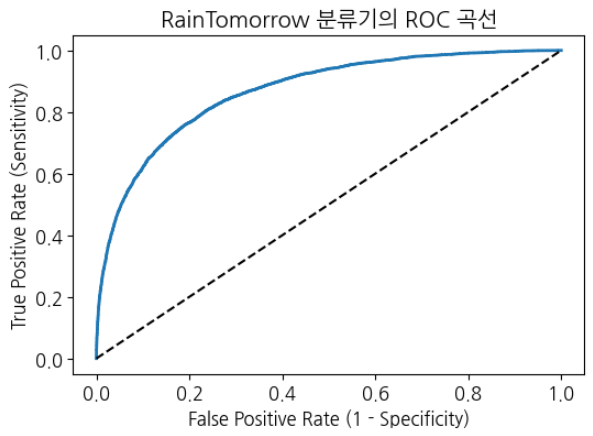
ROC Curve(ROC 곡선)
분류 모델 성능을 시각적으로 측정하는 또 다른 도구는 ROC 곡선입니다. ROC 곡선은 Receiver Operating Characteristic Curve(수신기 작동 특성 곡선)의 약자입니다. ROC 곡선은 다양한 분류 임계값 수준에서 분류 모델의 성능을 보여주는 도표입니다.
ROC 곡선은 다양한 임계값 수준에서 오탐률(FPR)에 대한 진양성률(TPR)을 플롯합니다.
진양성률(TPR)은 리콜이라고도 합니다. TP와 (TP + FN)의 비율로 정의됩니다.
오탐률(FPR)은 FP 대 (FP + TN)의 비율로 정의됩니다.
ROC 곡선에서는 단일 포인트의 TPR(진양성률)과 FPR(오탐률)에 초점을 맞출 것입니다. 이렇게 하면 다양한 임계값 수준에서 TPR과 FPR로 구성된 ROC 곡선의 일반적인 성능을 알 수 있습니다. 따라서 ROC 곡선은 다양한 분류 임계값 수준에서 TPR과 FPR을 그래프로 표시합니다. 임계값 수준을 낮추면 더 많은 항목이 양성으로 분류될 수 있습니다. 그러면 정탐(TP)과 오탐(FP)이 모두 증가합니다.
ROC 곡선은 특정 컨텍스트에 대한 민감도와 특이도의 균형을 맞추는 임계값 수준을 선택하는 데 도움이 됩니다.
ROC-AUC(Receiver Operating Characteristic - Area Under Curve)(수신기 작동 특성 - 곡선 아래 영역)
분류기 성능을 비교하는 기법입니다. 이 기법에서는 곡선 아래 면적(AUC)을 측정합니다. 완벽한 분류기는 ROC AUC가 1이고, 순수 무작위 분류기는 ROC AUC가 0.5입니다.
따라서 ROC AUC는 곡선 아래에 있는 ROC 플롯의 백분율입니다.
ROC AUC : 0.8671
Comments
-
ROC AUC는 분류기 성능을 단일 수치로 요약한 것입니다. 값이 높을수록 분류기가 더 우수하다는 것을 의미합니다.
-
우리 모델의 ROC AUC는 1에 가까워지고 있습니다. 따라서 내일 비가 올지 안 올지를 예측하는 데 있어 우리 분류기가 잘 작동한다고 결론 내릴 수 있습니다.
Cross validated ROC AUC : 0.8675
19. k-Fold Cross Validation(K-폴드 교차 검증)
Cross-validation scores:[0.84802784 0.84931683 0.84940277 0.84501353 0.84879474]
교차 검증 정확도는 평균을 계산하여 요약할 수 있습니다.
Average cross-validation score: 0.8481
당사의 오리지널 모델 점수는 0.8671으로 확인되었습니다. 교차 검증 평균 점수는 0.8481입니다. 따라서 교차 검증이 성능 향상으로 이어지지 않는다는 결론을 내릴 수 있습니다.
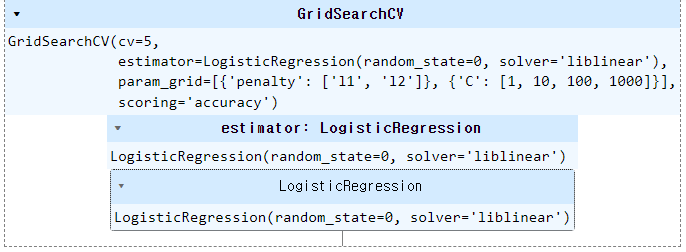
20. Hyperparameter Optimization using GridSearch CV(GridSearch CV를 사용한 하이퍼파라미터 최적화)
Parameters that give the best results :
{'penalty': 'l1'}
Estimator that was chosen by the search :
LogisticRegression(penalty='l1', random_state=0, solver='liblinear')
테스트 세트에서 GridSearch CV 점수 계산
GridSearch CV score on test set: 0.8488
Comments
원래 모델 테스트 정확도는 0.8483이고 GridSearch CV 정확도는 0.8488입니다.
이 특정 모델의 경우 GridSearch CV가 성능을 향상시킨다는 것을 알 수 있습니다.
21. Results and conclusion(결과 및 결론)
-
로지스틱 회귀 모델 정확도 점수는 0.8483입니다. 따라서 이 모델은 호주에 내일 비가 올지 여부를 예측하는 데 매우 효과적입니다.
-
내일 비가 올 것이라는 관측이 적습니다. 대부분의 관측은 내일 비가 내리지 않을 것이라고 예측합니다.
-
모델이 과적합의 징후를 보이지 않습니다.
-
C 값을 높이면 테스트 세트 정확도가 높아지고 훈련 세트 정확도도 약간 높아집니다. 따라서 더 복잡한 모델이 더 잘 수행되어야 한다는 결론을 내릴 수 있습니다.
-
임계값 수준을 높이면 정확도가 높아집니다.
-
우리 모델의 ROC AUC는 1에 접근합니다. 따라서 분류기가 내일 비가 올지 여부를 잘 예측한다고 결론을 내릴 수 있습니다.
-
원래 모델 정확도 점수는 0.8483인 반면 RFECV 후 정확도 점수는 0.8500입니다. 따라서 거의 비슷한 정확도를 얻을 수 있지만 기능 세트는 줄었습니다.
-
원래 모델에서 우리는 FP = 1183인 반면 FP1 = 1174입니다. 따라서 우리는 대략 같은 수의 잘못된 긍정을 얻습니다. 또한 FN = 3227인 반면 FN1 = 3091입니다. 따라서 위음성이 약간 높아집니다.
-
우리의 원래 모델 점수는 0.8483인 것으로 나타났습니다. 평균 교차 검증 점수는 0.8474입니다. 따라서 교차 검증이 성능 향상으로 이어지지 않는다는 결론을 내릴 수 있습니다.
-
원래 모델 테스트 정확도는 0.8483이고 GridSearch CV 정확도는 0.8488입니다. GridSearch CV가 이 특정 모델의 성능을 향상시키는 것을 볼 수 있습니다.


좋은 글 감사합니다.