문제
서울 지하철 2호선은 다음과 같이 생겼다.
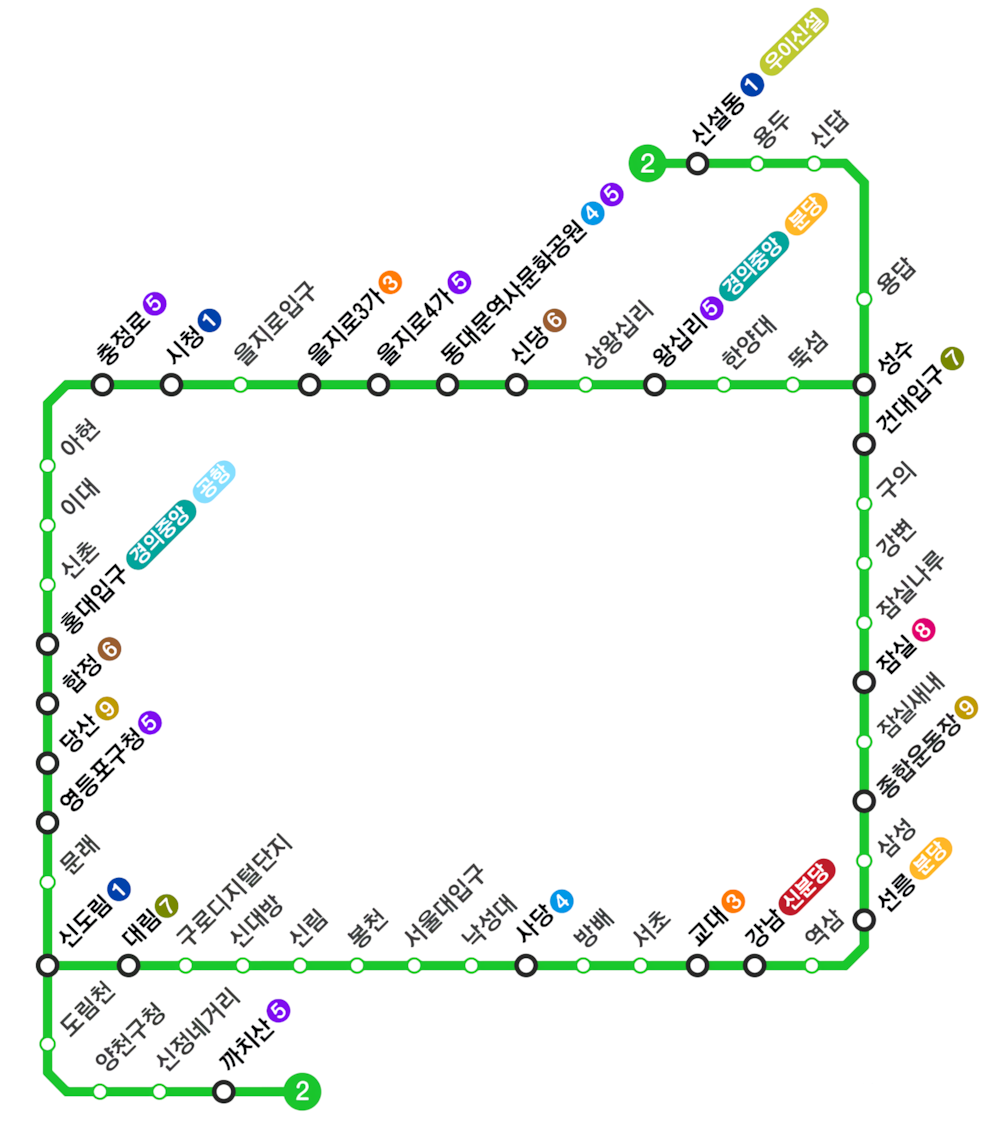
지하철 2호선에는 51개의 역이 있고, 역과 역 사이를 연결하는 구간이 51개 있다. 즉, 정점이 51개이고, 양방향 간선이 51개인 그래프로 나타낼 수 있다. 2호선은 순환선 1개와 2개의 지선으로 이루어져 있다. 한 역에서 출발해서 계속 가면 다시 출발한 역으로 돌아올 수 있는 노선을 순환선이라고 한다. 지선은 순환선에 속하는 한 역에서 시작하는 트리 형태의 노선이다.
두 역(정점) 사이의 거리는 지나야 하는 구간(간선)의 개수이다. 역 A와 순환선 사이의 거리는 A와 순환선에 속하는 역 사이의 거리 중 최솟값이다.
지하철 2호선과 같은 형태의 노선도가 주어졌을 때, 각 역과 순환선 사이의 거리를 구해보자.
입력
첫째 줄에 역의 개수 N(3 ≤ N ≤ 3,000)이 주어진다. 둘째 줄부터 N개의 줄에는 역과 역을 연결하는 구간의 정보가 주어진다. 같은 구간이 여러 번 주어지는 경우는 없고, 역은 1번부터 N번까지 번호가 매겨져 있다. 임의의 두 역 사이에 경로가 항상 존재하는 노선만 입력으로 주어진다.
출력
총 N개의 정수를 출력한다. 1번 역과 순환선 사이의 거리, 2번 역과 순환선 사이의 거리, ..., N번 역과 순환선 사이의 거리를 공백으로 구분해 출력한다.
🤔 생각
-
순환선과 역들 사이의 거리는 bfs로 해야한다는건 알겠다.
-
단 그 순환선을 어떻게 구할지가 문제다. dfs로 사이클 찾는 알고리즘을 짜면 되는거 같긴 한데..
-
문제는 내가 가물가물하다ㅜ 결국 100퍼센트 내 힘으로 풀진 못했고, 사이클 부분은 다른 사람 풀이를 공부하며 풀었다.
가장 이해가 잘 됐던 풀이
Embedded June님 블로그
📌 내 풀이
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**9)
def dfs(cv,pv):
if cache[cv] == 1: return cv
cache[cv] = 1
for nv in grid[cv]:
if nv == pv: continue # 양방향 그래프기 때문
result = dfs(nv,cv)
if result >= 0:
cache[cv] = 2
return result if cv != result else -1
return -1
def bfs():
q = []
for i in range(n):
if cache[i] == 2:
q.append(i)
dist[i] = 0
while q:
tmp = []
for cv in q:
for nv in grid[cv]:
if dist[nv] != -1: continue
dist[nv] = dist[cv] + 1
tmp.append(nv)
q = tmp
n = int(input())
grid = [[] for _ in range(n)]
cache = [0]*n
dist = [-1]*n
for _ in range(n):
a,b = map(int, input().split())
grid[a-1].append(b-1)
grid[b-1].append(a-1)
dfs(0,-1)
bfs()
print(*dist)
"""
0 : 미방문
1 : 방문
-1 : 사이클 x
2 : 사이클
"""
✔ 회고
- 사이클 탐지 알고리즘은 다섯 번 정도 다시 써본 것 같다. 이제 좀 내꺼가 된거 같다!
- 백트래킹도 좀 다시 손에 익혀야겠다.

