[논문 리뷰] Generative Adversarial Nets

Do ·2025년 3월 17일

목록 보기

9/9

이번 글에서는 "Deep learning(2017, MIT)"를 저술한 딥러닝 창시자 중 한명인 Ian J. Goodfellow가 2014년에 발표한 Generative Adversarial Nets(GAN)의 첫 논문을 읽고 리뷰하는 시간을 가져보겠습니다.

[초록]

우리는 "데이터 분포를 따라잡는 생성 모델(Generative model) G"와 "어떤 샘플이 G 모델이 생성한 데이터보다 실제 훈련 데이터에 속할 확률을 추정하는 판별 모델(Discriminative model) D"라는 두 가지 모델을 동시에 훈련시키는 적대적 과정을 통한 generative model을 추정하는 새 프레임워크를 제안한다.

G를 위한 훈련 절차는 D가 실수할 확률을 극대화하는 것이다. 이 프레임 워크는 minimax two-player game과 같다.

훈련 데이터의 분포를 밝혀내는 G가 있고 어디서든 $\frac{1}{2}$ 의 값을 가지는 D가 있는 G와 D의 임의의 공간에서, 유일한 해가 존재한다.

G와 D가 다층 퍼셉트론으로 정의되는 전체 시스템에서 역전파를 통해 학습된다. 이때는 Markov chain이나 unrolled approximate inference networks 와 같은 거는 필요없다.

최대최소 게임(minimax game)
1. 가짜와 진짜를 구별할 수 없게 만들기 vs 가짜와 진짜를 구별하기
2. 상대방이 자신의 이익을 최대화 하는 결정을 내릴 것이라고 행동을 예측하고 그 결과를 바탕으로 나의 이익을 최대화 하는 결정을 찾아야 함

[Introduction]

지금까지 딥러닝 분야에서 눈부신 발전은 Piecewise linear units을 활용한 역전파와 dropout 알고리즘에 기반하여 발전했다.

반면 Deep general models은 MLE(Maximum likelihood estimation) 과정에서 많은 상호작용의 확률적 계산에 대한 근사의 어려움과 Piecewise linear unit 활용의 어려움으로 인해 임팩트가 적었다.

이에 우리는 이러한 어려움을 회피할 수 있는 새로운 generative model 추정 절차를 제안한다.

제안된 adversarial nets 프레임워크에서 생성모델은 적으로 경쟁하게 한다. 판별 모델은 샘플이 생성모델에서 왔는지 실제 데이터에서 왔는지 결정하도록 배우게 한다.

예를 들면, 생성모델은 위조지폐를 생산하고 이를 걸리지 않고 사용하는 위조지폐범이다. 반면 판별모델은 위조지폐를 탐지해야하는 경찰이다.

이 게임에서 경쟁은 위조물건이 걸리지 않을 때까지 두 팀이 그들의 방법을 향상시키도록 이끌어준다.

이러한 프레임워크는 특정한 훈련 알고리즘을 보여준다.

생성 모델이 다층 퍼셉트론을 통해 랜덤 노이즈를 전달받아서 샘플을 생성하고 판별 모델도 다층 퍼셉트론을 이용하여 샘플이 진짜 데이터인지 생성 데이터인지 판별한다. 우리는 이러한 Special case를 adversarial nets라고 한다.

이 case에서 우리는 역전파와 드롭아웃 알고리즘을 활용하여 두 가지 모델을 훈련시킬 수 있다. 또한 오직 순전파만을 활용하여 생성모델에서 샘플을 생산하도록 할 수도 있다.

piecewise Linear Unit(PLU)

다음과 같은 ReLU 함수와 같은 활성화함수들이 모두 PLU에 해당한다.

[Adversarial nets]

adversarial modeling framework는 모델들이 이중 레이어 퍼셉트론일 때 똑바로 적용할 수 있다. 데이터 $x$ 의 생성자의 분포 $p_g$ 을 배우기 위해 우리는 입력 노이즈 변수 $p_z(Z)$ 를 정의할 수 있으며, $G(z;\theta_g)$ 라고 Data Space에 Mapping 하여 나타낼 수 있다. 이때, $G(z;\theta_g)$ 는 파라미터 $\theta_g$ 인 다중 퍼셉트론으로써 표현되는 미분가능한 함수 이다.

이어서, single scalar를 결과로 나타내는 $D(x;\theta_d)$ 라고 정의되는 다중 퍼셉트론도 정의할 수 있다. 이때 $D(x)$ 는 입력 데이터 $x$ 가 $p_g$ 가 아니고 실제 데이터일 확률을 표현한다.

이를 통해 모델을 정의했다면 다음은 모델을 훈련시키는 과정으로 넘어갑니다. 모델은 동시에 훈련시키며 각 모델의 학습 목표는 다음과 같습니다.

D : 학습 데이터셋과 G에서 만든 데이터에 correct label을 할당할 확률을 최대값으로 만드는 것
G : D가 correct label을 제대로 할당할 수 없을 정도로 학습 데이터셋과 유사한 데이터를 만드는 것. 논문에서는 이를 " $log(1-D(G(z)))$ 를 최소값으로 만들려는 것 $(log 1 = 0)$ "이라 말했습니다.

In other words,

$D$ 와 $G$ 는 two-player minimax game을 진행합니다. 이때 목적함수는 $V(G,D)$ 로 다음과 같이 정의합니다.

\min_G\max_D V(G,D) = E_{x \sim p_{data}(x)}[log D(x)]+E_{z \sim p_z(z)}[log(1-D(G(z)))]

이어서, 이러한 training criterion이 non-parametic limit 등등에서 $G$ 와 $D$ 가 데이터 생성 분포를 밝혀내는데 충분한 능력이 있다는 이론적 분석(theoretical analysis)을 보여주겠습니다.

위 그래프를 보면 이 방법에 대한 formal하진 않지만 교육적인 설명을 제공한다. 실질적으로 우리는 반복적이고 수학적인 접근으로써 이 게임을 구현해야한다. 훈련 과정 중 내부 loop에서 완료하는 것은 D를 최적화하는 것은 산술적으로도 불가하고 제한된 데이터셋에서는 과적합이 발생할 수도 있다. 그 대신에 우리는 $D$ 를 $k$ step 최적화하고, $G$ 를 one step 최적화하는 걸 번갈아 할 수 있다.

이러한 알고리즘은 $G$ 가 충분히 천천히 바뀌는 한 $D$ 를 최적해 주변에서 유지시켜준다.

In practice,

$V(G,D)$ 는 $G$ 가 잘 학습하도록 충분한 gradient를 제공하지 않을지도 모른다. $G$ 가 만약 잘 학습되지 않았다면 $D$ 는 높은 신뢰도(Confidence)를 가지고 샘플을 reject할 수 있다. 왜냐하면 그렇게 생성된 샘플들은 명백하게 훈련셋이랑 다르기 때문이다.

이러한 case에서 $log(1-D(G(z))$ 는 포화될 수 있다. 따라서 이럴 때는 $G$ 를 훈련시켜 $log(1-D(G(z))$ 를 최소화하는 게 아니라 $log(D(G(z))$ 를 최대화하도록 $G$ 를 훈련시킬 수 있다.

" $log(1-D(G(z))$ 는 포화될 수 있다." 의미: $G$ 에서 생성되는 Sample들이 명백하게 기존 데이터와 다르기 때문에 $D$ 에서는 이를 틀렸다고 판정하여 0에 가깝게 $D(G(z))$ 를 반환합니다.
하지만 D(G(z))가 0에 가까워지면, log(1−D(G(z)))는 0 근처에서 포화(saturate)되어 변화량이 작아지게 됩니다. 이 경우 기울기가 매우 작아지기 때문에 G는 효과적으로 학습되지 않습니다. 따라서, 대안 목적함수로 $log(D(G(z))$ 을 사용하여 학습을 진행합니다.

[figure 설명]

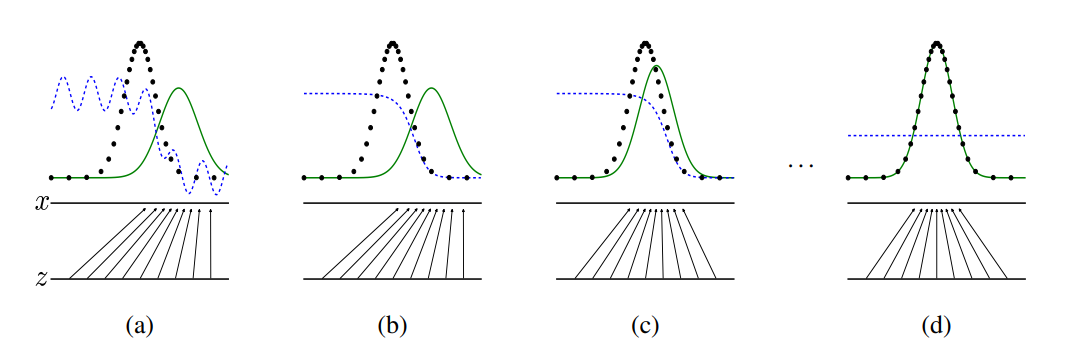
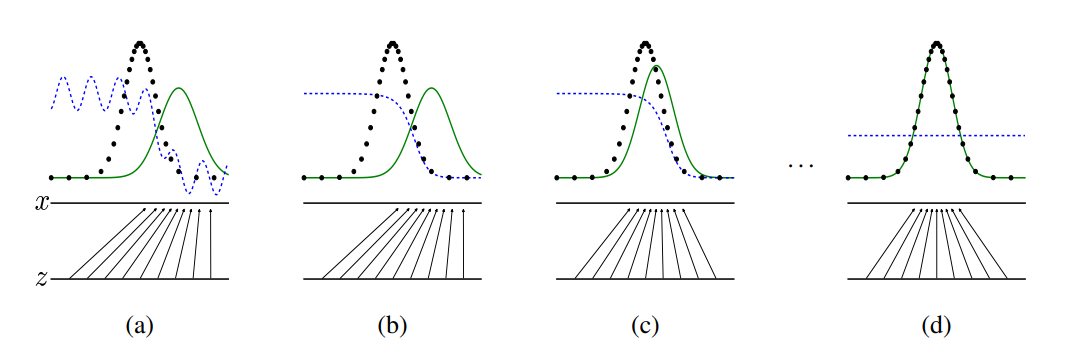
Generative adversarial nets는 Discriminative distribution( $D$ , blue, dashed line)를 업데이트 시킴과 동시에 훈련된다. 이는 $D$ 가 데이터 분포(black, dotted line, $p_x$ )의 sample과 생성된 분포인 $p_g$ (green, solid line)의 sample를 구별할 수 있도록 하면서 학습이 진행되기 때문이다.

figure에서 아래쪽 수평선은 $z$ 가 뽑히는 영역이고, 위 수평선은 $x$ 의 영역이다. 또한 화살표는 $x=G(z)$ 로 어떻게 매핑되는지를 보여준다.

$G$ 는 $p_g$ 의 고밀도 지역에서 수축하고, 저밀도 지역에서 확장된다. 그럼 단계별로 figure를 이해해보자.

(a): $p_g$ 와 $p_{data}$ 는 분포 자체는 비슷하고, $D$ 는 부분적으로 정확한 분류기이다.

(b) $D$ 의 내부 loop를 통해 $D$ 는 생성된 sample과 원본 data를 구별하고 $D$ 는 $D^*(x) = \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$ 에 수렴한다.

(d) 많은 훈련 step 후, 만약 $G$ 와 $D$ 가 충분한 효과를 가진다면 그들은 더이상 향상될 수 없는 지점( $p_g=p_{data}$ )에 이른다. 이때 판별모델(discriminator)는 두 분포를 다르게 판별할 수 없다. (이때, $D(x)=\frac{1}{2}$ )

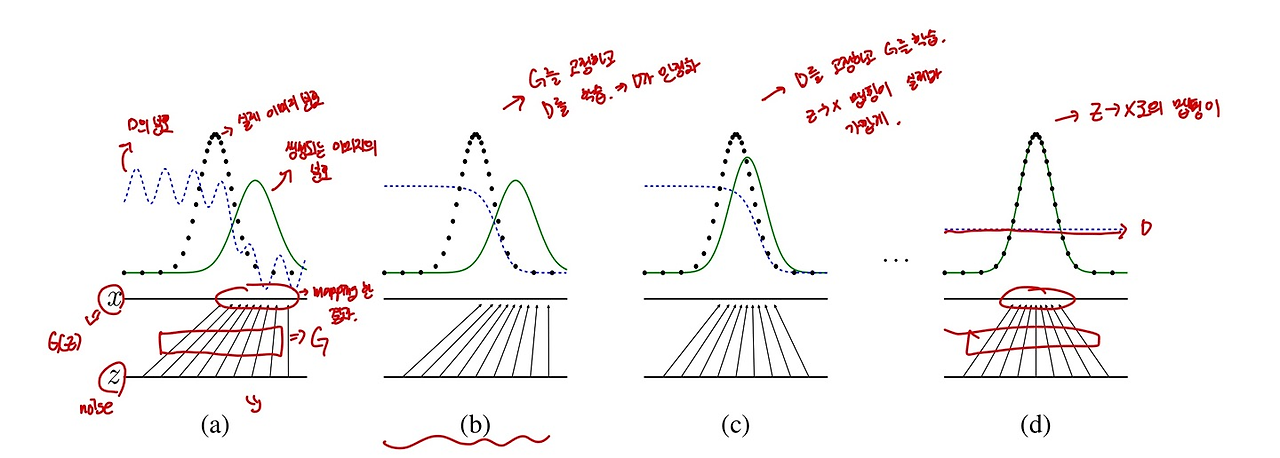
추가적으로 너무 잘 정리된 그림이 있어서 가지고 왔다.
출처: https://juniboy97.tistory.com/8

[Theoretical Results]

이 파트에선 위에서 제시된 GAN의 minmax game이 제대로 작동한다면, minmax game이 global minimum에서 unique solution 을 가지고 어떠한 조건에 만족하면 그 solution으로 수렴한다는 사실이 증명되어야 한다는 것을 수학적으로 입증하고 있습니다.

생성모델 $G$ 는 $G(z)$ 의 샘플 분포가 $z \sim p_z$ 일때 얻어지는 확률분포 $p_g$ 를 정의한다. 그러므로, $p_{data}$ 의 좋은 추정량으로 모이는 Algorithm 1은 충분한 훈련시간과 용량이 있다면 좋은 아이디어이다. 우리는 확률밀도함수 공간에서 수렴을 학습하는 모델의 무한한 능력을 제시한다.

[Global optimality of $p_g$ = $p_{data}$ ]

우리는 어떤 주어진 생성모델 $G$ 가 있을 때 최적 판별모델 $D$ 가 있다고 생각해보자

Proposition 1

$G$ 가 고정되었을 때, 최적 판별 모델 $D$ 은 다음과 같다.

D^*_G(x) = \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}

proof)

어떤 $G$ 가 주어졌을 때, 판별모델 $D$ 의 목적함수는 $V(G,D)$ 를 극대화하는 것이다.

V(G,D) = \int_x p_{data}(x)log(D(x))dx + \int_z p_z(z)log(1-D(G(z)))dz

= \int_x p_{data}(x)log(D(x)) + p_g(x) log(1-D(x))dx

이때 적분 속 식을, (a, b)가 (0,0)이 아닌 실수 순서쌍일 때 $alog(y)+blog(1-y)$ 라고 나타낼 수 있다. (즉, $p_{data}(x)$ 와 $p_g(x)$ 를 $a, b$ 로 상수 취급)

$alog(y)+blog(1-y)$ 을 미분하여 최댓값을 구하면 다음과 같다.

(alog(y)+blog(1-y))' \to \frac{a}{y} - \frac{b}{1-y} = 0

a - ay - by = 0 \to (a+b)y = a

y^* = \frac{a}{a+b}

따라서, $y$ 가 $\frac{a}{a+b}$ 일 때 최대이므로 다음과 같이 나타낼 수 있다.

D^*_G(x) = \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}

이를 다시 $V(G,D)$ 에 대입하면 다음과 같이 식이 전개된다.

C(G) = E_{x \sim p_{data}}[log D^*_G(x)] + E_{x \sim p_g}[log(1-D^*_G(x))]

= E_{x \sim p_{data}}[log \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}] + E_{x \sim p_g}[log\frac{p_g(x)}{p_{data}(x)+p_g(x)}]

Theorem 1

The global minimum of the virtual training criterion C(G) is achieved if and only if pg = p{data}. At that point, C(G) achieves the value $-log4$

proof)

For $p_g = p_{data}$ , $D^*_G(x) = \frac{1}{2}$

그러므로, $D^*_G(x) = \frac{1}{2}$ 라면 위 식을 통해 다음과 같음을 파악할 수 있다.

C(G) = -log2 + (-log2) = -log4

그러므로 $C(G)$ 의 가장 좋은 가능한 값을 보기 위해 우리는 다음과 같음을 관찰해야한다.

C(G) = E_{x \sim p_{data}}[-log2] + E_{x \sim p_g}[-log2] = -log 4

이때 해당 식을 다음과 같이 바꿀 수 있다.

C(G) = E_{x \sim p_{data}}[log \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}] + E_{x \sim p_g}[log\frac{p_g(x)}{p_{data}(x)+p_g(x)}] + log4 - log4

$log4$ 를 반으로 나누어 각 항에 다음과 같이 더해준다.

C(G) = (E_{x \sim p_{data}}[log \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}] + log2) \\+ (E_{x \sim p_g}[log\frac{p_g(x)}{p_{data}(x)+p_g(x)}] + log2) - log4

= E_{x \sim p_{data}}[log \frac{p_{data}(x)\times2}{p_{data}(x)+p_g(x)}] + E_{x \sim p_g}[log\frac{p_g(x) \times2}{p_{data}(x)+p_g(x)}] - log4

이때 KL Divergence는 다음과 같은 식으로 구성되는데,

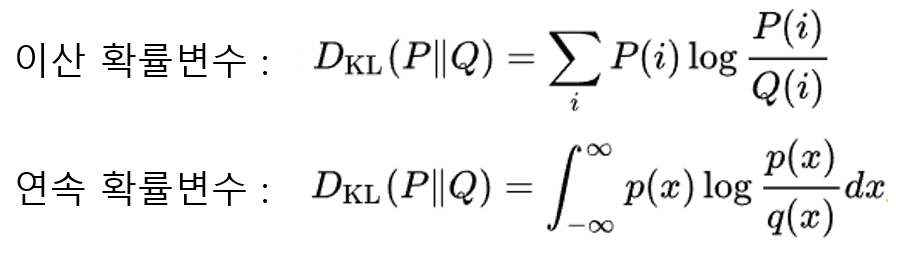
이를 위 식에 적용하면 $p(i) = p_{data}(x), Q(i) = \frac{p_{data}(x) + p_g(x)}{2}$ 과 같은 방식으로 첫 항과 두번째 항에 적용할 수 있다.

그럼 다음과 같은 식이 도출된다.

C(G) = -log4 + KL(p_{data} ||\frac{p_{data}+p_g}{2})+KL(p_{g} ||\frac{p_{data}+p_g}{2})

이때 KL은 Kullback-Leibler divergence(쿨백 라이블러 발산)이다.

위 식에 다음 Jensen-Shannon divergence(JSD)을 적용할 수 있다.

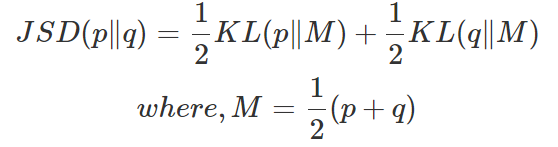
따라서 최종적으로 다음과 같은 식으로 도출된다.

C(G) = -log4 + 2 \times JSD(p_{data} || p_g)

이때 JSD는 두 distribution이 일치할 때 0이 된다.
따라서 $C(G) = -log4$ 가 $C(G)$ 의 Global minimum이고, unique Solution은 $p_g = p_{data}$ 일 때이다.

즉, two-player minimax game의 global optimality는 $p_g = p_{data}$ 뿐이다.

그러므로, data generating process를 완벽하게 복제하는 모델이 완성된다!

[정보이론 정리]

Kullback-Leibler divergence를 이해하기 위해선 부연 설명이 필요할 것 같아서 중간 단원을 나눴다.

정보량

통계학에서 정보량이란 "깜놀도"이라고 쉽게 이해할 수 있다. 많이 등장하는 변수의 경우 해당 정보의 희소성이 적다. 즉 정보량이 적다.

확률이 낮은 사건일수록 거의 일어나지 않을 일이기 때문에 정보량은 높다.

예를 들어 (1,1) 주변 점들이 많고, (10, 13)이라는 점이 하나 있는 산점도가 있을 때 (1,1) 주변 점들 각각의 정보량은 (10, 13)에 있는 점보다 적다는 의미이다. 이를 수학적으로 다음과 같이 나타낸다.

따라서, 정보량은 다음과 같이 나타낼 수 있다.

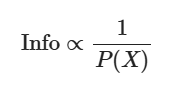
조금 더 구체적으로, 통계학에서 정보량은 다음과 같이 정의한다.
이산 랜덤변수 $X$ 에 대해,

I(x) = -log_b(P(X))

이때, 로그의 밑 b는 응용 분야에 따라 다르게 쓸 수 있는데, 대게 b는 2, e, 10 중 하나를 사용할 수 있다. (각각을 사용했을 때의 정보량의 단위는 bit, nit, dit이다).

왜 로그를 통해 정보량을 정의하냐면 정보에 대한 아래의 개념들을 만족시킬 수 있는 수식이어야 하기 때문이다.

1) 확률값(혹은 확률밀도 값)에 반비례 해야 하기 때문.

2) 두 사건의 정보량을 합치면 각 사건의 정보량을 합친 것과 같아야 함.

그리고 음수인 것은 로그함수를 사용했기 때문에 반비례로 만들어주기 위해 사용하였다.

출처: https://angeloyeo.github.io/2020/10/26/information_entropy.html

Entropy

통계학에서 엔트로피란 평균 정보량을 얘기한다. 엔트로피는 "정보량이 생산되는 과정에서, 이를 표현하는데 필요한 최소 자원량의 기댓값"이다.

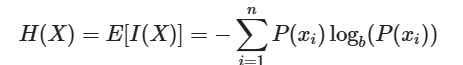
다음과 같은 수식으로 표현되는데,

이는 특정 정보량을 표현하는데, 특정 확률변수의 확률이 높으면 ( $p_i$ 가 높으면), 해당 확률변수를 표현할 자원량( $log (1/p_i)$ ) 이 줄어들게 된다는 것을 의미한다.

Cross Entropy

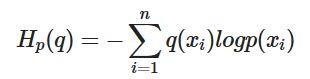
엔트로피에서 두 확률분포의 차이를 구하기 위해 사용되는 게 크로스 엔트로피다.

엔트로피 식과 비교했을 때 확률과 정보량이 서로 다른 분포라는 차이가 있다.

즉 entropy는 확률분포 P를 따르는 환경에서 정보량이 생산될 때, 이를 표현하는데 필요한 최소 자원량의 기댓값이며,

corss entropy는 확률분포 P를 각각 따르는 환경에서 정보량이 생산될 때, 확률분포 Q를 따르는 환경이라 생각하고 정보량을 표현하는데 필요한 자원량의 기댓값인 것이다.

Kullback-Leibler divergence

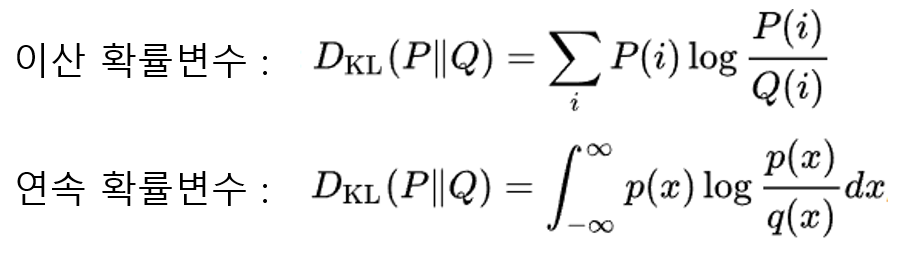
위키백과에서 Kullback-Leibler divergence은 어떠한 확률분포 P가 있을 때, 샘플링 과정에서 그 분포를 근사적으로 표현하는 확률분포 Q를 P 대신 사용할 경우 엔트로피 변화를 의미한다.

그렇다. 엔트로피 변화이므로, 엔트로피에서 크로스 엔트로피를 뺀 값이 바로 KL Divergence이다. 즉, 현재 분포에서 다른 분포로 바꾸기 위한 비용이 바로 KL Divergence다.

이렇게 KL divergence의 의미를 이해하고 나면, KL divergence의 두가지 대표적인 특징도 쉽게 이해할 수 있다.

1) KL divergence의 값은 0이상이다.

2) KL divergence의 값은 asymetric 하다.

우선, H(p) 값이 최소 자원량의 기댓값이므로, H(p)는 무조건 H(p, q)보다 작을 수 밖에 없다. 따라서 H(p, q) - H(p) 인 KL divergence 의 값이 항상 0 이상인 것이다.

또한, p와 q의 위치가 바뀌면 KL divergence의 값 또한 바뀌게 된다. 따라서 KL divergence의 값은 symetric 하지 않고, asymetric 하다는 것을 확인할 수 있다.

출처: https://ddongwon.tistory.com/118

Jensen-Shannon divergence

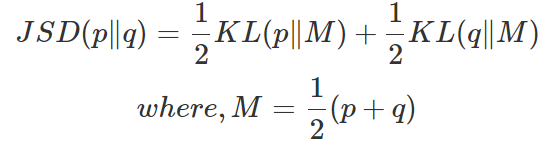
KL Divergence는 asymetric하다는 특징이 있기 때문에 "거리"의 개념으로 사용하기에는 부적절하다. 따라서 $p, q$ 의 평균을 사용하여 Symmetric한 JSD를 사용한다면 "거리"의 개념으로 사용할 수 있다.

최종적으로 도출된

C(G) = -log4 + 2 \times JSD(p_{data} || p_g)

이때 JSD는 두 distribution이 일치할 때 0이 되므로, $p_g = p_{data}$ 일 때
따라서 $C(G) = -log4$ 가 $C(G)$ 의 Global minimum이 된다.

Proposition2

if $G$ and $D$ have enough capacity, and at each step of Algorithm 1, the discriminator is allowed to reach its optimum given G, and $p_g$ is updated so as to improve the criterion

C(G) = E_{x \sim p_{data}}[log D^*_G(x)] + E_{x \sim p_g}[log(1-D^*_G(x))]

then $p_g$ converges to $p_{data}$

이는 Algorithm 1을 통해 생성자의 분포 $p_g$ 가 점차 실제 데이터 분포 $p_{data}$ 에 수렴하는지를 보장하는지에 대한 증명이다.

즉, GAN이 적절히 학습된다면 G(생성자)가 만들어낸 데이터 분포가 실제 데이터 분포와 같아질 수 있음을 증명하는 부분이다.

proof)
$V(G,D) = U(p_g, D)$ 를 $p_g$ 의 함수로 생각해보자

$U(p_g, D)$ 는 $p_g$ 에서 convex, convex function의 편미분 값은 최댓값을 얻을 수 있는 지역을 포함한다.

만약 다음 식과 같고,

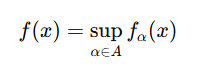
$f_{\alpha}(x)$ 가 모든 $\alpha$ 에 대해 $x$ 에서 convex할 때 다음과 같다면,

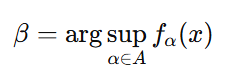
다음 식이 성립한다.

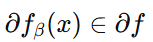
이는 최적 판별모델 $D$ 가 $p_g$ 에 대해 경사하강법을 수행하는 것과 같다. 그러므로 Theorem 1에서 보았듯이 $\sup_D U(p_g, D)$ 는 $p_g$ 에 대해 convex하며, 유일한 global optimum을 가진다. 그러므로 $p_g$ 가 조금씩 충분하게 업데이트가 된다면 $p_g$ 는 $p_x$ 로 수렴한다.

In practice,

GAN은 $p_g$ 의 전체적인 분포를 학습하기 보다는 $p_g$ 의 limited family를 학습할 뿐이다. 즉 $p_g$ 보다는 $\theta_g$ 를 조정하여 최적화한다.

따라서 $G$ 를 정의하는 다층 퍼셉트론을 사용하는 것은 parameter space에서 여러 개의 임계점(critical point)를 발생시킬 수 있다. 즉, 학습이 제대로 안될 수 있다.

하지만, 실용적으로 다층 퍼셉트론은 뛰어난 성능을 보이고 있으므로 이론적으로 완벽한 보장이 없더라도 충분히 실용적인 모델임을 확인할 수 있다.

공부하는 사람