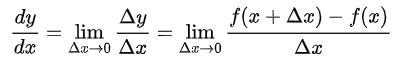[선형대수 기초] Chapter 1 미분

머신러닝을 공부함에 있어서 수학을 공부하는 것은 필수적이다.
그래서 선형대수학의 기초를 공부하고자 이번 시리즈를 시작하였습니다.
고등학교 수준의 기본적인 수학을 학습했음을 전제로,
최대한 이해하기 쉽게 내용을 구성하고자 노력하였습니다.
이 글을 보시는 분들이 수학 공부를 함에 있어서 도움이 되면 좋겠습니다.

이번 시리즈는 도서 "통계학을 위한 선형대수"(박흥선)을 참고하였습니다.

[학습개요]

• 학습목적
• 미분함수(Derivative)
• 편미분함수(Partial Derivative)
• 헤시안행렬(Hessian Matrix)
• 최적점과 안장점(Optimal and Saddle)
• 제약 조건 하의 최적점 찾기(라그랑지 승수법)

[학습목적]

머신러닝 모델에 대한 공부를 할 때 미분이 왜 중요할까??
도함수를 미분하는 것과 머신러닝 모델이라... "미분을 배워봤자 기초만 알고 있으면 되는 거 아닌가??"와 같은 안일한 생각들로 머신러닝 공부와 미분을 공부하는게 어떠한 연관성이 있는지 잘 감이 오지 않을 수 있다.

하지만 미분은 매우매우x100 중요하다.
나는 공부를 무작정 많이 하는 것도 중요하지만, 이 공부가 내가 이루려는 목적에서 왜 중요한지 알고 공부해야한다고 생각하기 때문에 미분을 공부하는 목적부터 다루겠다.

그래서 미분이 머신러닝을 공부함에 있어서 왜 중요하냐?
왜냐하면 내가 생각한 수학적인 관점에서 <머신러닝>의 정의는
"데이터의 차원을 축소하여 모델을 실제 데이터에 맞게 최적화시키는 것"이기 때문이다.

이를 알기 쉽게 말하면 "최소한의 변수로 실제 데이터와 오차가 제일 작은 모델을 만드는 것"이고,
더 쉽게 말하면 "데이터의 열을 최대한 줄여 오차가 제일 작은 모델을 만드는 것"이기 때문이다.

이 정의는 다음과 같은 두 가지 문제를 가진다.
1. 차원축소
2. 최적화

물론, 모델이 이해하기 쉬운 데이터 형태로 바꾸는 과정에 대한 이해도 필요하지만 난 위 두 가지 문제가 머신러닝 공부를 함에 있어서 가장 중요하다고 생각한다.

그리고 둘 중에서도 특히 더 중요한 건 최적화이다.

그리고, 최적화에서 가장 중요한 문제는 Gradient-Based Optimization 문제!
즉 Cost Function을 가장 작게 만드는 것이다.
여기서 미분과 머신러닝 공부의 연관점을 찾을 수 있다.

Cost function을 작게 만든다. 즉, 함수가 최소가 되게 만든다.
그렇다.

수학적으로 최소/최대를 찾는 가장 대표적인 방법이 바로 미분이다.
그러므로 머신러닝을 공부함에 있어서 가장 핵심적인 개념을 다루는 도구가 미분이기 때문에 머신러닝을 공부할 때 미분을 배우는 것이다!

그럼 이제 미분에서 중요한 개념들을 함께 공부해보자

[미분함수와 편미분함수]

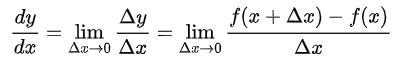
함수 f(x)의 변화율은 x의 작은 변화에 대해 x가 어떻게 변화하는가를 계산함으로 얻을 수 있다.

그러므로 미분함수는 다음과 같이 정의된다.

이때 최대/최소점은 $f'(x) = 0$이 되는 점을 찾아냄으로써 찾을 수 있다.

자 그럼 편미분함수, Partial Derivative는 무엇인가.

다변량함수 $f(x_1,x_2)$에 대한 미분은 각 변수에 대한 편미분함수로 구성되며 다음과 같이 정의된다.

그리고 이를 벡터로 표시하면 다음과 같이 나타낼 수 있다.

$\nabla f =\begin{pmatrix} \frac{\partial f}{\partial x_1}\\ \frac{\partial f}{\partial x_2}\end{pmatrix}$

이를 $f(x_1,x_2)$의 스코어벡터(score vector) 혹은 기울기벡터(gradient vector)라고 하며, 이때 $\nabla$는 델 연산자라고 부른다.

[헤시안행렬(Hessian Matrix)]

헤시안행렬은 위의 델연산자를 2차 미분함수로 나타내어 Matrix 형태로 표현한 것이라고 쉽게 말할 수 있으며, 함수 $f(x,y)$의 헤시안 행렬은 다음과 같이 정의된다.

$H(x,y) = \begin{pmatrix} \frac{\partial^2f}{\partial x^2}&\frac{\partial^2f}{\partial x \partial y}\\ \frac{\partial^2f}{\partial y \partial x}&\frac{\partial^2f}{\partial y^2}\end{pmatrix}$

이러한 헤시안 행렬은 아래의 자코비안(Jacobian) 행렬과도 연관성을 가지는데, 두 식을 비교해보면 알 수 있듯이 자코비안 행렬의 2차 도함수 버전이 헤시안행렬임을 알 수 있다.

$J = \begin{pmatrix} \frac{\partial f_1}{\partial x_1}& \cdots &\frac{\partial f_1}{\partial x_n}\\ \vdots&\ddots&\vdots\\ \frac{\partial f_m}{\partial x_1}&\cdots&\frac{\partial f_m}{\partial x_n}\end{pmatrix}$

이와 같은 헤시안행렬은 최적화 문제에서 매우 중요한 개념으로 꼽힌다.

[최적점(optimal)과 안장점(saddle)]

"최적화" 과정에서 함수의 최적점(최대 혹은 최소)을 나타내는 극값에 대한 문제는 자연과학과 공학, 사회과학 등 여러 다양한 분야에서 중요하다.

이에 극대값(Local maximum)과 극소값(Local minimum)을 가지는 조건에 대해 알아보고자 한다.

고등학교 수학을 공부하던 그 시절의 기억을 잘 되짚어보면, 단변량 함수의 극대값과 극소값은 다음과 같이 구할 수 있다.

단변량함수 f(x)에 대해, $x=x_0$에서

$\frac{df(x_0)}{dx} = 0 ,\frac{d^2f(x_0)}{dx^2}<0$

을 만족하면 $f(x_0)$은 극대값이며, 한편

$\frac{df(x_0)}{dx} = 0 ,\frac{d^2f(x_0)}{dx^2}>0$

을 만족하면 $f(x_0)$은 극소값이 된다.

그럼 다변량 함수의 극대값과 극소값은 어떻게 구할 수 있을까?

다변량 함수의 극대값과 극소값 다음 두 가지 조건이 성립할 때 만족된다.

1. ${\frac{\partial f(x_0,y_0)}{\partial x}} = {\frac{\partial f(x_0,y_0)}{\partial y}} = 0$
2. $(\frac{\partial^2 f(x_0,y_0)}{\partial x^2})(\frac{\partial^2 f(x_0,y_0)}{\partial y^2}) -(\frac{\partial^2 f(x_0,y_0)}{\partial x \partial y})^2 > 0$

일 때,

$\frac{\partial^2 f(x_0,y_0)}{\partial x^2}+\frac{\partial^2 f(x_0,y_0)}{\partial y^2} < 0$이면, $f(x_0,y_0)$은 극대값이고
$\frac{\partial^2 f(x_0,y_0)}{\partial x^2}+\frac{\partial^2 f(x_0,y_0)}{\partial y^2} > 0$이면, $f(x_0,y_0)$은 극소값이다.

그런데 여기서 하나의 궁금증이 생긴다.

단변량 함수의 극값 조건과 다변량 함수의 극값 조건을 비교해보면 단변량 함수에서 $\frac{df(x_0)}{dx} = 0$ 조건이 다변량 함수에서의 ${\frac{\partial f(x_0,y_0)}{\partial x}} = {\frac{\partial f(x_0,y_0)}{\partial y}} = 0$ 과 같은 성질의 조건이고,

단변량함수에서 $\frac{d^2f(x_0)}{dx^2}<0$,$\frac{d^2f(x_0)}{dx^2}>0$이라는 조건은 다변량함수에서 $\frac{\partial^2 f(x_0,y_0)}{\partial x^2}+\frac{\partial^2 f(x_0,y_0)}{\partial y^2} < 0$,$\frac{\partial^2 f(x_0,y_0)}{\partial x^2}+\frac{\partial^2 f(x_0,y_0)}{\partial y^2} > 0$과 같은 성질의 조건임을 알 수 있다.

그럼 $(\frac{\partial^2 f(x_0,y_0)}{\partial x^2})(\frac{\partial^2 f(x_0,y_0)}{\partial y^2}) -(\frac{\partial^2 f(x_0,y_0)}{\partial x \partial y})^2 > 0$이라는 조건은 무슨 의미를 가지는 걸까?

바로, 위에서 배웠던 헤시안 행렬이 양정치 행렬(positive definite matrix)1임을 의미한다. 즉, 헤시안 행렬이 양정치 행렬이라면 다변량함수에서의 극대값과 극소값을 구할 수 있게 되는 것이다.

• 다변량 함수의 극대점

  

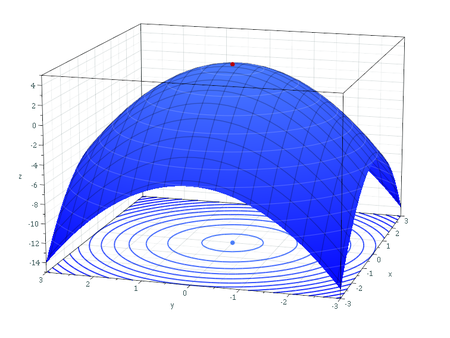
그러면 헤시안행렬이 꼭 양정치행렬이여만 할까?
당연히 아니다. 다음은 헤시안행렬이 음정치행렬인 경우이다.

1. ${\frac{\partial f(x_0,y_0)}{\partial x}} = {\frac{\partial f(x_0,y_0)}{\partial y}} = 0$
2. $(\frac{\partial^2 f(x_0,y_0)}{\partial x^2})(\frac{\partial^2 f(x_0,y_0)}{\partial y^2}) -(\frac{\partial^2 f(x_0,y_0)}{\partial x \partial y})^2 < 0$

다변량 함수 $f(x,y)$가 $(x_0,y_0)$에서 위 두 조건을 만족시킬 때, $f(x_0,y_0)$를 안장점(Saddle point)라고 부른다.

안장점이란 극대/극소값은 아니지만, 미분값이 0이면서도 극값을 이루지 않는 점으로, 이 점에서 한 변수 방향에서는 극대값을 이루지만, 다른 변수 방향에서는 극소값을 이룬다.

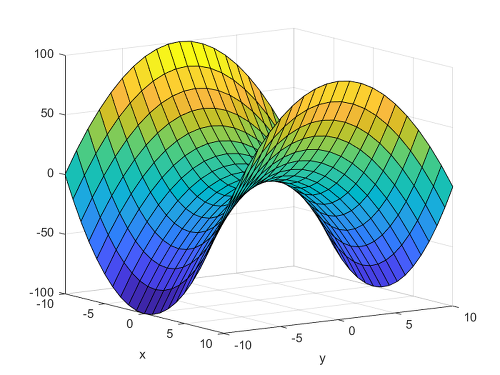
그리고 만약

이라면 점$(x_0,y_0)$은 아무것도 결정할 수 없는(indecisive) 점이 된다.

이러한 최적점과 안장점은 최적화 문제에서 중요한 개념이니 꼭 숙지하도록 하자

[제한된 조건에서 최적점 찾기]

위에선 아무런 제약조건 없이 함수의 극대/극소점을 찾는 방법을 살펴보았지만, 실제로 극대/극소점을 어떤 특정 제약조건 안에서 찾는 경우가 흔히 발생한다. 이때 쓰이는 방법이 라그랑지 승수법(Langrange multiplier)을 통한 제약조건 하 극값 계산법이다.

라그랑지 승수법은 제약조건 $g(x,y,z) = c$ 하에서의 함수 $f(x,y,z)$의 극대/극소값은 아래 조건을 만족시킨다.

$Q(x,y,z) = f(x,y,z) - \lambda(g(x,y,z)-c)$에서

$\frac{\partial Q}{\partial x} = \frac{\partial Q}{\partial y} = \frac{\partial Q}{\partial z} = \frac{\partial Q}{\partial \lambda} = 0$

여기서 Q를 라그랑지 함수, $\lambda$를 라그랑지 승수라고 일컫는다.
해당 식을 통해 제약조건 하에서 극대/극소점을 해결할 수 있다.

• 각주
  1: 양정치 행렬에 관해선 다음에 다룰 예정이다.↩