알고리즘 개념 정리📖 (3) 트리, 힙, 그래프, DFS & BFS, Dynamic Programming

자료구조 개념 정리하기 <3>

🖍🖍 알고리즘 백준 문제 마라톤에 문제 주제에 맞춰서 정리해본거라 중구난방일 수 있지만.. 최대한 내가 이해한대로! 알고리즘 튜터님(스파르타 코딩클럽 박현준 튜터님😆)이 집어주신 전체적인 자료구조의 숲을 보는 훈련을 하면서 정리하는게 목표입니다!

---

🌲 자료구조의 숲 보기

• Tree 우리가 알아 둘 건 이진 트리 와 완전 이진 트리(배열로 표현 가능)!
• Heap 최댓값, 최솟값 빠르게 찾을 때!
• Graph 연결 관계 표현에 초점이 맞춰져 있는 비선형 자료구조!
• DFS & BFS DFS는 깊이 우선이어서 제일 깊은 level 갔다가 다시 올라오고, BFS는 너비 우선 이라 같은 level에 있는 걸 다 보고 다음 level로!
• Dynamic Programming 복잡한 문제를 간단하게 나눠서 해결 하는 것. 재귀와 비슷 하지만 이미 찾아 놓은 답은 기록 해 둠으로서 시간 완전 절약!

---

🌿 트리

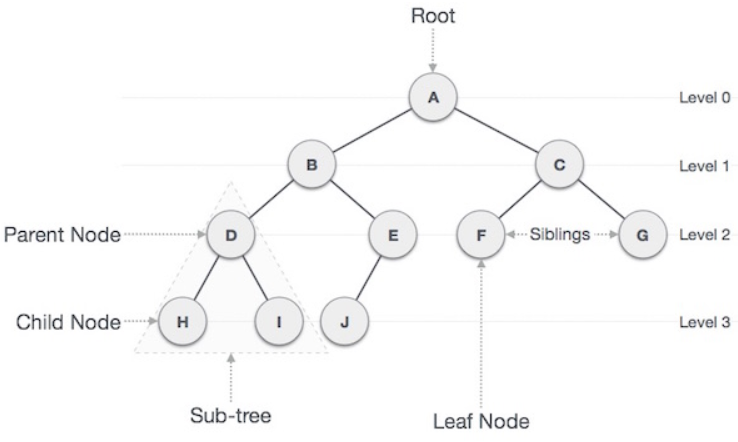
• 거꾸로 세워놓은 나무 처럼 생긴 계층형 비선형 자료구조 입니다!

• 이진 트리(Binary Tree) : 각 노드가 최대 두개 의 자식을 가집니다! (0, 1, 2개 까지만 가질 수 있어요!)

• 완전 이진 트리(Complete Binary Tree) : 이진 트리 중에서 노드를 삽입 할 때, 왼쪽 최하단 부터 채워져야 합니다! 배열로 표현이 가능 합니다!

• 완전 이진 트리를 배열로 바꿀 때
  1) 트리를 구현할 때는 편의상 배열의 0번째 index는 사용되지 않습니다!
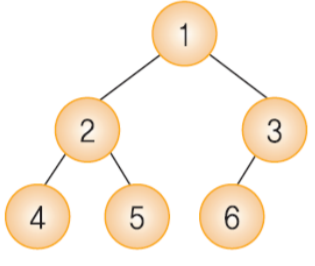
  2) 아래와 같은 트리를 배열로 표현하면 [None, 1, 2, 3, 4, 5, 6] 입니다! 배열을 보고 트리 구조를 표현하려면 현재 인덱스 * 2 -> 왼쪽 자식의 인덱스, 현재 인덱스 * 2 + 1 -> 오른쪽 자식의 인덱스, 현재 인덱스 // 2 -> 부모의 인덱스 라고 생각하면 됩니다!

• 완전 이진 트리 높이
  이후에 시간복잡도를 계산할 때 사용하는 데, 노드이 개수가 N개인 완전 이진 트리의 최대 높이는 O(log(N)) 입니다!

🌻 힙

• 트리 구조를 알아야 되는 이유라고 생각 합니다!

• 데이터에서 최대값Max-Heap과 최소값Min-Heap을 빠르게 찾기 위해 고안된 완전 이진 트리 입니다! 이렇게 빠르게 찾으려면 정렬에서 처럼 힙도 규칙을 지켜줘야 빠르게 최댓값(또는 최솟값)을 찾을 수 있습니다! 그 규칙은 (max-heap에서) 부모 노드의 값이 자식 노드의 값보다 항상 커야한다! 입니다!

• Max Heap에 원소 추가하기 code
  일단 max heap의 중요한 규칙인 힙은 항상 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있어야 한다! 를 지켜줘야 합니다!
  1) 먼저 맨마지막에 추가할 원소를 넣어주고
  2) 규칙이 성립할 때까지 부모노드와 비교하면서 자리를 바꿔줍니다!
  3) cur_index 가 1이 되면 root가 된거라 다른 것과 비교를 안해도 됩니다! 따라서 비교하는 반복문은 cur_index > 1 일 때 까지만!

    class MaxHeap:
        def __init__(self):
            self.items = [None]

        def insert(self, value):
            self.items.append(value)
            cur_index = len(self.items) - 1
            while cur_index > 1:
                parent_index = cur_index // 2
                if self.items[cur_index] > self.items[parent_index]:
                    self.items[cur_index], self.items[parent_index] = self.items[parent_index], self.items[cur_index]
                    cur_index = parent_index
                else: 
                    break
            return

• Max Heap에 원소 제거하기 code
  max heap에서 원소를 제거할 때는 스택과 같이 맨 위의 원소만 제거할 수 있습니다!🤔 또한 원소를 추가할 때처럼 힙은 항상 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있어야 한다! 규칙을 지켜줘야 합니다!
  1) 루트 노드를 삭제하기 위해 루트 노드와 맨 마지막 노드를 교체합니다!
  2) 맨 마지막 노드(원래 루트 노드)를 삭제합니다! 나중에 삭제 하고 나서 이 노드의 값을 반환해주기 위해 변수에 저장해 둡시다!
  3) 원래 루트 노드가 아닌 다른 노드가 루트가 되면서 규칙이 깨져있을 수 있습니다! 규칙이 지켜질 때까지 자식 노드와 비교하면서 자리를 찾습니다!
  4) 마지막으로 삭제하기 전에 저장해 놓은 원래 루트 노드 값을 반환합니다!

    def delete(self):
            delete_node = self.items[1]
            self.items[1], self.items[-1] = self.items[-1], self.items[1]
            self.items.pop()
            cur_index = 1
            while cur_index < len(self.items):
                left_child_index = cur_index * 2
                right_child_index = cur_index * 2 + 1
                max_index = cur_index

                # 왼쪽 자식이 더 크면 max_index를 왼쪽 자식 index로 갱신해주고
                if left_child_index < len(self.items) and self.items[left_child_index] > self.items[max_index]:
                    max_index = left_child_index
                # 오른쪽 자식이 더 크면 max_index를 오른쪽 자식 index로 갱신해주고
                if right_child_index < len(self.items) and self.items[right_child_index] > self.items[max_index]:
                    max_index = right_child_index
                # 왼쪽, 오른쪽 자식과 비교했는데도 max_index가 그대로 cur_index와 같으면 제대로 된 자리에 있는 것
                if max_index == cur_index:
                    break

                # 갱신된 max_index의 값과 cur_index의 값 교체
                # 부모노드가 자식 노드 보다 더 작아서 바꿔주는 과정이 이것!
                self.items[cur_index], self.items[max_index] = self.items[max_index], self.items[cur_index]
                cur_index = max_index


            return delete_node

---

🌐 그래프

• 노드간의 연결관계를 표현해주는 비선형 구조의 자료구조입니다!

• 무방향 그래프와 유방향 그래프가 있는데 강의에서 배운 무방향 그래프 를 간단하게 정리해 볼게요!

• 그래프를 표현하는 방법은 두가지가 있습니다!
  1) 인접 행렬(Adjacency Matrix): 2차원 배열로 연결관계를 나타냅니다! ex) A, B가 연결되어 있으므로 1, A와 E는 연결이 안되어 있으므로 0 => 어떤게 연결되어 있는지 확인이 바로 되지만 모든 조합의 연결여부를 저장해야 되므로 O(Node^2) 만큼의 공간이 사용됩니다!
  
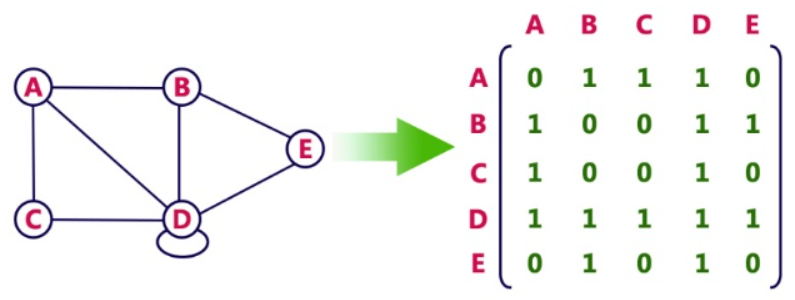
  2) 인접 리스트(Adjacnecy List): Linked List로 연결관계를 나타냅니다! 위의 그림을 인접리스트에서 dictionary 로 표현하면 아래와 같습니다!

      graph = {
          A: [B, C, D],
          B: [A, D, E],
          C: [A, D]
          D: [A, B, C, D, E]
          E: [B, D]
      	}

=> 어떤 Node가 연결되어 있는지 알아 내려면 최대 O(Edge^2) 만큼의 시간을 사용해야 하는 대신 모든 연결여부를 저장할 필요가 없으므로 O(Edge + Node) 만큼의 공간을 사용하면 됩니다!

---

🗻 DFS(Depth First Search)

• 트리나 그래프를 탐색하는 방법 중 하나로, 한 노드를 시작으로 인접한 다른 노드를 재귀적으로 탐색하는데, 가장 깊은 단계에 있는 노드 탐색 후 다시 위로 올라가서 탐색 을 반복합니다!

• 깊게 파고드는 거라 공간은 적게 쓰지만, 최단 경로 탐색이 어렵습니다!

• stack을 이용한 DFS구현 code
  인접한 노드중 방문하지 않은 노드를 stack에 넣고, 가장 마지막에 넣은 노드들만 꺼내서 탐색 합니다!(stack을 쓰는 이유)
  1) 루트 노드를 스택에 넣고 현재 위치하고 있는(처음은 루트 노드) 노드를 빼서 visited에 추가합니다!
  2) 현재 방문한 노드의 인접한 노드중에 방문하지 않은(visited에 없는) 것만 stack 추가 합니다!
  3) 1) 과 2) 를 스택이 완전히 비어질 때까지 반복합니다!

    # 인접 리스트 방식으로 그래프 표현!
    graph = {
        1: [2, 5, 9],
        2: [1, 3],
        3: [2, 4],
        4: [3],
        5: [1, 6, 8],
        6: [5, 7],
        7: [6],
        8: [5],
        9: [1, 10],
        10: [9]
    }


    def dfs_stack(adjacent_graph, start_node):
        stack = [start_node]
        visited = []

        while stack: 
            cur_node = stack.pop()
            visited.append(cur_node)
            for adj_node in adjacent_graph[cur_node]: 
                if adj_node not in visited:
                    stack.append(adj_node)
        return visited


    print(dfs_stack(graph, 1))  # 1 이 시작노드입니다!
    # [1, 9, 10, 5, 8, 6, 7, 2, 3, 4] 이 출력!

---

⛺ BFS (Breadth First Search)

• 넓이 우선 탐색 을 뜻하는 BFS도 트리와 그래프를 탐색하는 방법이지만 DFS와는 다르게 인접한 노드를 모두 탐색한 뒤 다음 level을 탐색합니다!

• 최단 경로를 쉽게 찾을 수 있지만, 모든 분기(인접 노드)를 다 저장하면 공간을 많이 쓰고 시간이 더 오래 걸릴 수 있습니다!

• queue를 이용한 BFS 구현 code
  현재 인접한 노드 부터 방문한다 는 노드 중 방문하지 않은 노드들을 모두 저장해 두고, 가장 처음에 넣은 것부터 순서대로 탐색한다 는 뜻입니다! queue 를 사용하는 이유가 됩니다!
  1) DFS와 거의 비슷하게, 먼저 루트 노드를 큐에 넣고 그 노드가 현재 있는 곳이므로 visited 에 넣습니다!
  2) 현재 방문해 있는 노드와 인접한 노드 중 방문하지 않은(visited에 없는) 노드를 큐에 추가합니다!
  3) 1)과 2)를 큐가 완전히 비어질때까지 반복합니다!

    # 인접 리스트 방식으로 표현!
    graph = {
        1: [2, 3, 4],
        2: [1, 5],
        3: [1, 6, 7],
        4: [1, 8],
        5: [2, 9],
        6: [3, 10],
        7: [3],
        8: [4],
        9: [5],
        10: [6]
    }

    def bfs_queue(adj_graph, start_node):
        queue = [start_node]
        visited = []

        while queue:
            cur_node = queue.pop(0)
            visited.append(cur_node)
            for adj_node in adj_graph[cur_node]:
                if adj_node not in visited:
                    queue.append(adj_node)
        return visited

---

🤸‍♀️🤸‍♂️ Dynamic Programming

• 여러개의 하위 문제를 풀고 그 결과를 이용해 문제를 해결하는 알고리즘 입니다!

• 재귀와 비슷하게 문제를 쪼개서 정의 할 때 쓰는 방법인데 여기서 가장 크고 중요한 차이는 바로 한번 나온 결과는 기록해두고 나중에 그 결과값이 필요 할때 기록해 둔것을 불러온다!! 입니다!

• 위와 같이 결과를 기록하는 걸 memoization 이라고 하는 데, 이 과정으로 이미 구한 값도 다시해야되는 재귀에 비해 시간이 훨씬 단축됩니다!!

• DP로 구현하는 피보나치 수열 code

  input = 50

    #memo 라는 변수에 Fibo(1)과 Fibo(2) 값을 저장해놨습니다!
    memo = {
        1: 1,
        2: 1
    }


    def fibo_dynamic_programming(n, fibo_memo):
            # linked list에서 따로 key 값이라 분류하지 않아도
            # 아래와 같이 n 이라는 key가 fibo_memo에 있는지 간단하게 확인 가능!
            if n in fibo_memo:
                return fibo_memo[n]
            else:
                nth_fibo = fibo_dynamic_programming(n - 1, fibo_memo) + fibo_dynamic_programming(n - 2, fibo_memo) 
                # 기록되어 있지 않은 새로운 값이므로 기록해두기! = memoization!
                fibo_memo[n] = nth_fibo
                return nth_fibo


    print(fibo_dynamic_programming(input, memo))

---

🧾 알고리즘 문제 풀기

🎲 DFS 와 BFS

🎲 계단 오르기