알고리즘 개념 정리📖 (2) 정렬, 스택, 큐, 해쉬

자료구조 개념 정리하기 <2>

🖍🖍 알고리즘 백준 문제 마라톤에 문제 주제에 맞춰서 정리해본거라 중구난방일 수 있지만.. 최대한 내가 이해한대로! 알고리즘 튜터님(스파르타 코딩클럽 박현준 튜터님😆)이 집어주신 전체적인 자료구조의 숲을 보는 훈련을 하면서 정리하는게 목표입니다!

---

🌲 자료구조의 숲 보기

• Sort는 오름차순 또는 내림차순 으로 정리. 버블정렬(단순이 다 비교), 선택정렬(선택에서 앞으로 이동 시키기), 삽입정렬(필요할 때만 자리 이동, 아니면 break => 이미 정렬이 좀 되어 있으면 빠름) , 병합정렬(쪼개서 정렬하고 합친다, 시간 비교적 빠름) 각각 차이 알아두기!
• Stack은 Last In First Out으로 DFS에 사용! 뭔가 넣었다가 바로 빼는 느낌!
• Queue 은 First In First Out으로 BFS에 사용! 순서대로 빼는 느낌!
• Hash 파이썬에서 dictionary와 같고 다른 언어에서는 흔히 object(객체)와 비슷한 개념! key값과 value가 존재! 정리해서 묶어 놓을 때 좋음!

🧱 정렬

버블 정렬

• 옆에 거랑 비교하면서 큰 수가 마지막으로 가게끔 자리를 계속 바꿔 줍니다!

• 시간 복잡도는 for문 안에 하나의 for문이 더 있으므로 O(N^2)

• 버블 정렬 code
  1) 일단 비교를 몇 번 해야 할지 생각 해보고
  2) 맨 마지막 까지 비교가 끝나면, 맨 마지막 숫자는 제대로 정렬 된 거니깐 그 다음 비교는 그걸 제외하고 하면 됩니다! 즉, 배열의 길이가 5라면 처음엔 array[4] 까지 비교하고 그 과정이 끝나면 array[4]는 정렬이 완료된 것이고 그 다음은 array[3]까지만 비교하면 되는 방식 입니다!

   input = [4, 6, 2, 9, 1]
   
   def bubble_sort(array):
        n = len(array)
        for i in range(n - 1):
            for j in range(n - i - 1):
                if array[j] > array[j + 1]:
                    array[j], array[j + 1] = array[j + 1],array[j]
        return array

선택 정렬

• 처음부터 마지막까지 비교해보고 제일 작은 수를 맨 앞으로 자리를 바꿔줍니다!

• 똑같이 2차 반복문이 나오고, array의 길이 만큼 반복하므로 O(N^2)

• 선택 정렬 code
  1) 일단 이렇게 비교하는 행위를 총 몇번해야하는 지 생각 합니다. 예를들어 list에 수가 5개 있으면, 처음에는 4번 (4와6, 4와2, 2와9, 9와1), 이렇게 비교해서 제일 작은 수를 맨앞으로 보내면, 맨 앞은 이미 정렬이 완료된 것입니다! 그러면 맨 처음을 제외한 나머지 숫자 4개는 3번 비교, 그 다음은 2번, 마지막 1번 이렇게 총 4번을 합니다! => 그러므로 큰 반복문은 n - 1
  2) 비교 할 때마다 맨 앞자리가 갱신 되므로 (맨 처음에는 array[0], 그다음은 array[1]...) => min_index = i
  3) 1)에서 설명했듯이 실질적으로 비교하는 횟수는 맨 처음에 4번, 그다음 3번 이런식이므로 i가 1씩 커질 때마다 비교해야하는 범위가 줄어 듭니다. => 그래서 작은 반복문은 n - i
  4) 2)에서 설명했듯이 맨 앞자리가 갱신되고 거기서 부터 비교를 다시 시작하므로 => array[i + j]
  5) 그리고 맨 앞과 비교한 수 중 가장 작은 수 자리 변경!
  

  input = [4, 6, 2, 9, 1]
  
  def selection_sort(array):
      n = len(array)
      for i in range(n - 1):
          min_index = i
          for j in range(n - i):
              if array[i + j] < array[min_index]:
                  min_index = i + j
          array[i], array[min_index] = array[min_index], array[i]       
      return

삽입 정렬

• 선택 정렬과 가장 큰 차이는 비교해보고 필요 할때만 자리를 이동 시킵니다!

• 이것도 똑같이 O(N^2) 이 지만, 만약 정렬이 거의 되어있는 list라면? break 문에 의해서 금방 끝나게 되므로 최선의 경우에는 Ω(N)

• 삽입 정렬 code
  1) 비교 자체는 똑같이 n - 1 번 입니다.
  2) 이번에는 비교횟수가 점점 늘어납니다. 예를 들어 맨 앞에 4가 있고 6이 들어온다고 했을 때, 4와 6만 비교하면 되서 1번, 6다음으로 2가 들어온다고 하면 6과 2, 4와 2 비교하면 되서 2번 입니다. => 이렇게 비교하는 횟수가 1씩 늘어나므로 j의 범위는 i 로 정해줘서 하나씩 늘어 나게 하고, 맨 처음 부터 비교 한번을 하므로 i의 범위를 1부터 n으로 합니다. 그럼 n - 1과 똑같은 횟수가 됩니다!
  3) 앞에 있는 수가 뒤에 있는 수보다 크면 둘의 자리를 바꿔 줍니다. 여기서 만약 바로 앞에 있는 수가 더 크지 않으면 더 앞에 있는 수와는 비교할 필요가 없습니다! 이미 앞은 정렬이 되어있으니까요! 예를 들어, [2, 4, 6, 9, 1]의 경우가 9가 새로 들어온다고 가정했을 때, 6과 9를 비교하면 이미 6이 9보다 작으므로 앞에 2와 4도 당연히 9보다 작다는 걸알 수 있습니다. 따라서 이런경우에는 더 비교하지 않고 break! 삽입 정렬의 가장 큰 특징 이라고 할 수 있어요!

  input = [4, 6, 2, 9, 1]

  def insertion_sort(array):
      n = len(array)
      for i in range(1, n):
          for j in range(i):
              if array[i - j - 1] > array[i - j]:
                  array[i - j - 1], array[i - j] = array[i - j], array[i - j - 1]                
              else:
                  break
      return

병합 정렬

• 배열을 앞부분과 뒷부분으로 쪼개서 정렬하고 병합하는 과정을 반복합니다!

• 시간 복잡도는 O(NlogN)

• 병합 code
  1) 일단 merge 함수는 두개로 쪼개진 (정렬된)list가 각각 있을 때, 각각의 원소를 하나씩 비교해서 크기가 작은 거를 새로운 result list에 추가해 줍니다. 이렇게 더 작은 걸 가지고 있던 list는 그 다음 원소를 비교할 수 있도록 index를 +1 해줍니다 => array1 요소를 result list에 추가해주면 i += 1, array2면 j += 1
  2) 한 list가 먼저 끝나면 나머지 list에 있는 원소들을 그대로 result list에 마저 추가해 줍니다

  array_a = [1, 2, 3, 5]
  array_b = [4, 6, 7, 8]


  def merge(array1, array2):
      result = []
      i = 0
      j = 0
      while i < len(array1) and j < len(array2):
          if i < len(array1) and array1[i] <= array2[j]:
              result.append(array1[i])
              i += 1
          elif j < len(array2) and array1[i] > array2[j]:
              result.append(array2[j])
              j += 1
      if i == len(array1):
          while j < len(array2):
              result.append(array2[j])
              j += 1
      if j == len(array2):
          while i < len(array1):
              result.append(array1[i])
              i += 1
      return result


  print(merge(array_a, array_b)) 

• 병합 정렬 code
  1) 일단 큰 list를 두 개로 쪼개고 그 list를 정렬 시킨 뒤 merge 함수를 사용해서 합칩니다.
  2) 쪼개고, 정렬하고, 쪼개고 정렬하고... 이럴때 바로 재귀 를 사용합니다!! => 최종적으로 list의 길이가 1이거나 0일 땐 무조건 정렬된 list라고 할 수 있습니다! 이부분이 탈출 조건이 됩니다!

    array = [5, 3, 2, 1, 6, 8, 7, 4]
    
    def merge_sort(array):
      if len(array) <= 1:
          return array
      mid = len(array) //2
      left_list = array[:mid]
      right_list = array[mid:]
      return merge(merge_sort(left_list), merge_sort(right_list))

---

🛒 스택

• Last In First Out 제일 나중에 들어간게 제일 먼저 나옵니다!

• 넣은 순서가 필요한 경우 스택 사용! ex) 뒤로가기 버튼

• data를 넣고 빼는 게 빈번? Linked List 비슷!

• 스택 직접 구현하는 code

  class Node:
      def __init__(self, data):
          self.data = data
          self.next = None


  class Stack:
      def __init__(self):
          self.head = None
          
	  # 맨 앞에 새로운 Node추가
      def push(self, value):
          new_node = Node(value)
          new_node.next = self.head
          self.head = new_node
          return
	  
      # 제일 나중에 들어간걸 제일 먼저 나오게 하므로
      # 맨 앞에 있는 것 반환
      def pop(self):
          if self.is_empty():
          	  return "Stack is empty!"
          delete_node = self.head
          self.head = self.head.next
          return delete_node

      def peek(self):
          if self.is_empty():
          	  return "Stack is empty!"
          return self.head.data

      # isEmpty 기능 구현
      def is_empty(self):
          return self.head is None

---

🏃‍♀️ 큐

• First In First Out 먼저 들어간게 먼저 나옵니다!

• 따라서, 순서대로 처리 되어야 하는 일에 필요! ex) 주문 들어온 순서 대로 처리, 먼저 해야 하는 일 저장

• stack은 한쪽에서 넣고 빼고를 다하지만, queue는 한쪽에서 넣고 다른 한쪽에서 뺄 수 있습니다!

• stack 처럼 넣고 빼고가 빈번하므로 Linked List 와 비슷하게 구현!

• 큐 직접 구현하는 code

  class Node:
      def __init__(self, data):
          self.data = data
          self.next = None

  class Queue:
      def __init__(self):
          self.head = None
          self.tail = None

	  # 맨 뒤에 새로운 node 추가하기
      def enqueue(self, value):
          new_node = Node(value)
          if self.is_empty():
              self.head = new_node
              self.tail = new_node
              return
          self.tail.next = new_node
          self.tail = new_node
          return
          
	  # 큐는 맨 앞에 있는게 맨 먼저 들어간 것이므로
      # head를 삭제 => 제일 먼저 들어간게 제일 먼저 나온다
      def dequeue(self):
          if self.is_empty():
              return "Queue is empty"
          delete_node = self.head
          self.head = self.head.next
          return delete_node.data

      def peek(self):
          if self.is_empty():
              return "Queue is empty"
          return self.head.data

      def is_empty(self):
          return self.head is None

🤔 실제 문제를 풀 때는 ?
stack과 queue 개념을 이용하기 위해 직접 구현해봤지만 문제를 풀때는 파이선의 list를 쓰면 됩니다.
stack.append(4) => push(4)
stack.pop(4) => pop(4)
queue.pop(0) => dequeue()

---

🧵 해쉬

• 파이썬의 dictionary 와 거의 같습니다!

• key를 통해서 value 를 불러옵니다!

• 하지만 dictionary는 내부적으로 array(배열)을 사용하므로 어떤 index에 특정한 값을 넣어줄지를 정해야 합니다! 그 때 사용하는 것이 바로 해쉬함수 입니다!

  👀 Hash function ?
  임의의 길이를 갖는 메세지를 입력하면 고정된 길이의 해쉬값을 출력하는 함수 입니다! ex) hash("fast") = -146084012848775433

• 해쉬 함수를 사용해서 나온 값은 너무 크므로 그 값을 list의 길이로 나눈 나머지 값을 index로 해줍니다! 어떤 수든 나누는 수 보다 나머지가 작기 때문에 가능합니다!

• 해쉬 code

  class Dict:
      def __init__(self):
          self.items = [None] * 8

      def put(self, key, value):
          index = hash(key) % len(self.items)
          self.items[index] = value
          return

      def get(self, key):
          index = hash(key) % len(self.items)
          return self.items[index]

• 그런데 이대로만 하면 문제가 발생합니다! 해쉬값을 나눴을 때 나머지 같으면 같은 index에 여러가지 data가 들어가려다가 먼저 들어가있던 data를 나중에 들어오는 data가 덮어 쓸 수 있습니다😂 그러므로 이럴 때는 한 index에 data를 넣되, 예쁘게 정리해서 즉, linked list로 연결해서 넣어줍니다! 이렇게 겹치는 현상을 충돌 이라 하고 아래 그림 처럼 Linked List를 이용해서 충돌을 해결하는 걸 체이닝 이라고 합니다!

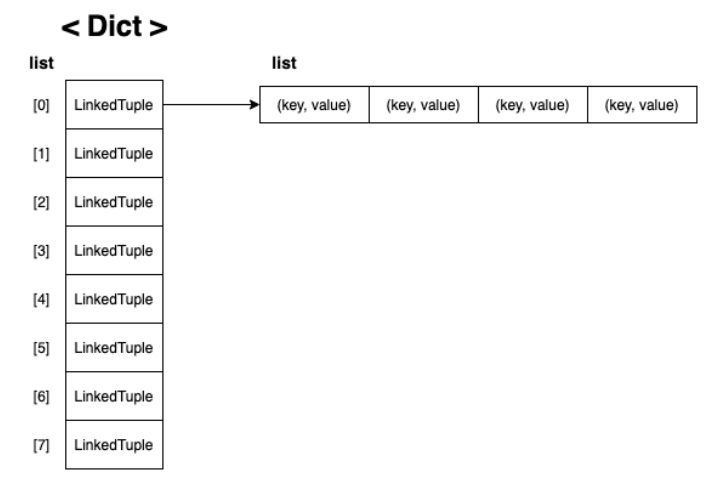
• 체이닝 적용시킨 해쉬 code

  class Dict:
      def __init__(self):
          self.items = [None] * 8

      def put(self, key, value):        
          index = hash(key) % len(self.items)
          # 이미 index에 다른 data가 있다면 그 뒤에 붙여주자!
          return self.items[index].add(key, value)

      def get(self, key):
          index = hash(key) % len(self.items)
          # 한 index에 여러 data가 있다면 key로 value를 가져오자!
          return self.items[index].get(key)

🧾 알고리즘 문제 풀기

🎲 좌표 정렬하기 2

🎲 괄호

🎲 스택 수열

🎲 회전하는 큐

🎲 통계학