동차좌표계의 필요성

이동변환을 왜 굳이 축을 하나 더 추가해서 곱셈으로 하지?에 관해,
축을 추가하지 않고 하려면

void LocationCalculation(float dx, float dy)
{
	x = x + dx;
	y = y + dy;
}

void RotationCalculation()
{
	//회전 로직
}

void ScaleCalculation()
{
	//크기 변환 로직
}

int main()
{
	float Matrix = {0.f, 0.f};
    LocationCalculation(2.f, 3.f);
    RotationCalculation();
    ScaleCalculation();
}

이렇게 메인 함수에서 세 개의 함수를 만들어 주고 호출해야함.

하지만 동차좌표계를 사용하면 세 가지의 로직을 합칠 수 있음.

//가시성을 위해 .f 생략
float LocCal = 	{{1, 0, dx},
				 {0, 1, dy},
           		 {0, 0,  1}};

float RotCal = {{cos, -sin, 0},
				{sin,  cos, 0},
           		{0  ,    0, 1}};
                
float ScaCal = {{a, 0 ,0}
				{0, b, 0}
           		{0, 0, 1}};

전부 곱해주면(순차적으로 곱해주면)

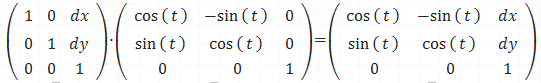
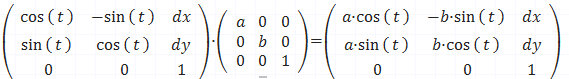
이런 행렬이 나온다.

결과적으로 하나의 행렬 안에 원하는 값을 넣어주고, 원래의 좌표값 '앞에' 넣어 곱해주면
한 번에 원하는 것만 골라서 이동, 회전, 크기변환이 가능해진다.

float a = 1.f;	//x축 배율
float b = 1.f;	//y축 배율
float t = 0.f;	//회전각
float dx = 0.f;	//x 이동
float dy = 0.f;	//y 이동
float PI = 3.1415926535f;
//위에서 초기화 해주고 나서, 원하는 값만 다시 넣어주면 될 듯?

a = 2.f;
t = 30.f * PI / 180.f;
dx = 2.f;
dy = 3.f;

float TotalCal = 	{{a*cos(t), -b*sin(t), dx},
					{a*sin(t),   b*cos(t), dy},
                    {0       ,   0       , 1 }};

엄청 편해보인다!

근데 3차원으로 가니까 하나도 안 편해보인다..

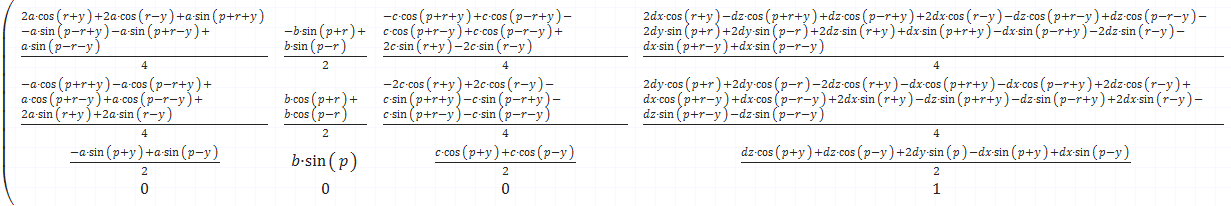
2차원에서는 이동x크기x회전 이렇게 3개만 곱해주면 되는데,
3차원에서는 이동x크기x요x피치x롤 이렇게 5개를 곱해줘야 해서 복잡해진다.