[Algorithm] 정렬 : Counting sort(계수 정렬), Radix sort(기수 정렬)

정렬 시리즈는 계속 된다.
이번은 counting sort(계수 정렬), radix sort(기수 정렬)에 대해 학습하고 정리한다.

1. Counting sort : 계수 정렬

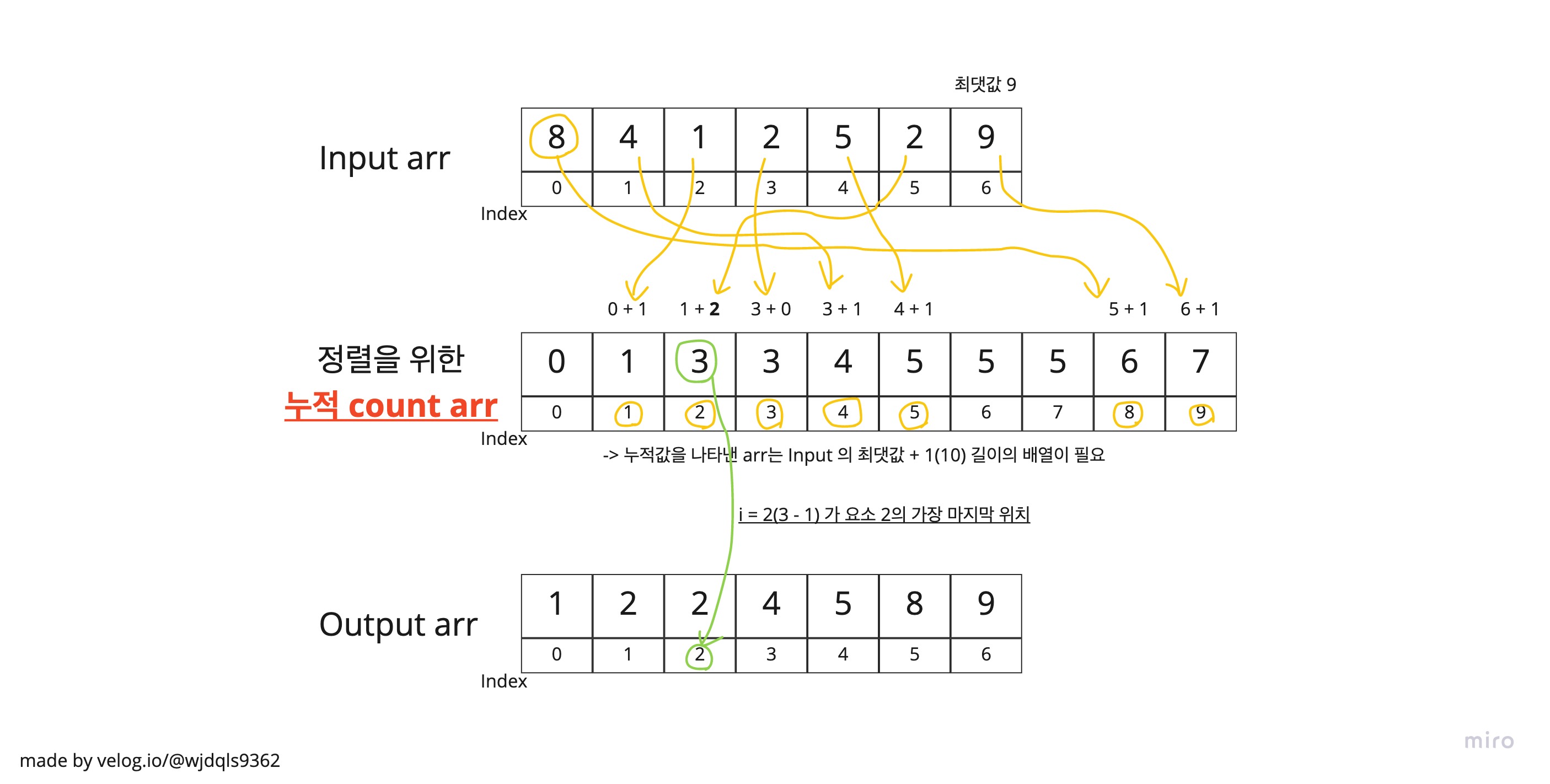
Counting sort(계수 정렬)는 각 요소의 배열 등장 횟수를 count해 누적합으로 나타내는 배열을 만든 뒤, 그 누적합으로 요소들의 index를 알아내 작은 숫자 순서대로 정렬하는 기법이다.
비교 정렬이 아니기 때문에 O(n + k) 라는 특이한 시간 복잡도를 가진다. k는 Input 요소의 최댓값인데, k가 작은 수라면 O(n)이겠지만, k가 무한으로 커질 때는 O(무한)이 될 수도 있다.
따라서 요소의 최댓값에 영향을 받는 알고리즘이다.
( O(n + k) : n or k 라는 뜻으로, n이 클지 k가 클지 아직 모름 )

앞서 언급했듯, Input arr의 요소 중 최솟값 ~ (최댓값 - 1) 길이 만큼의 누적합 배열(혹은 객체)을 필요로 하는 정렬 기법이므로 요소 간 차이가 크거나, 최댓값 요소가 매우 클 경우 메모리 낭비가 심한 경우가 생길 수 있다.

function countingSort(arr) {
  const max = Math.max(...arr);
  const min = Math.min(...arr);
  let count = {}; // 누적합 나타내는 객체 사용
  
  for (let i = min; i <= max; i += 1) {
    count[i] = 0; // min부터 max까지 0으로 채운 객체 준비
  }
  for (let i = 0; i < arr.length; i += 1) {
    count[arr[i]] += 1; // arr를 순회하며 요소 개수 적립
  }
  
  let sortedArr = [];
  for (let i = min; i < max; i += 1) {
    while (count[i] > 0) { // count값이 0이 될때까지 정렬배열에 요소 삽입
      sortedArr.push(i); // 요소 삽입 후 
      count[i] --; // count값 -- 처리
    }
  }
  
  return sortedArr;
};

2. Radix sort : 기수 정렬

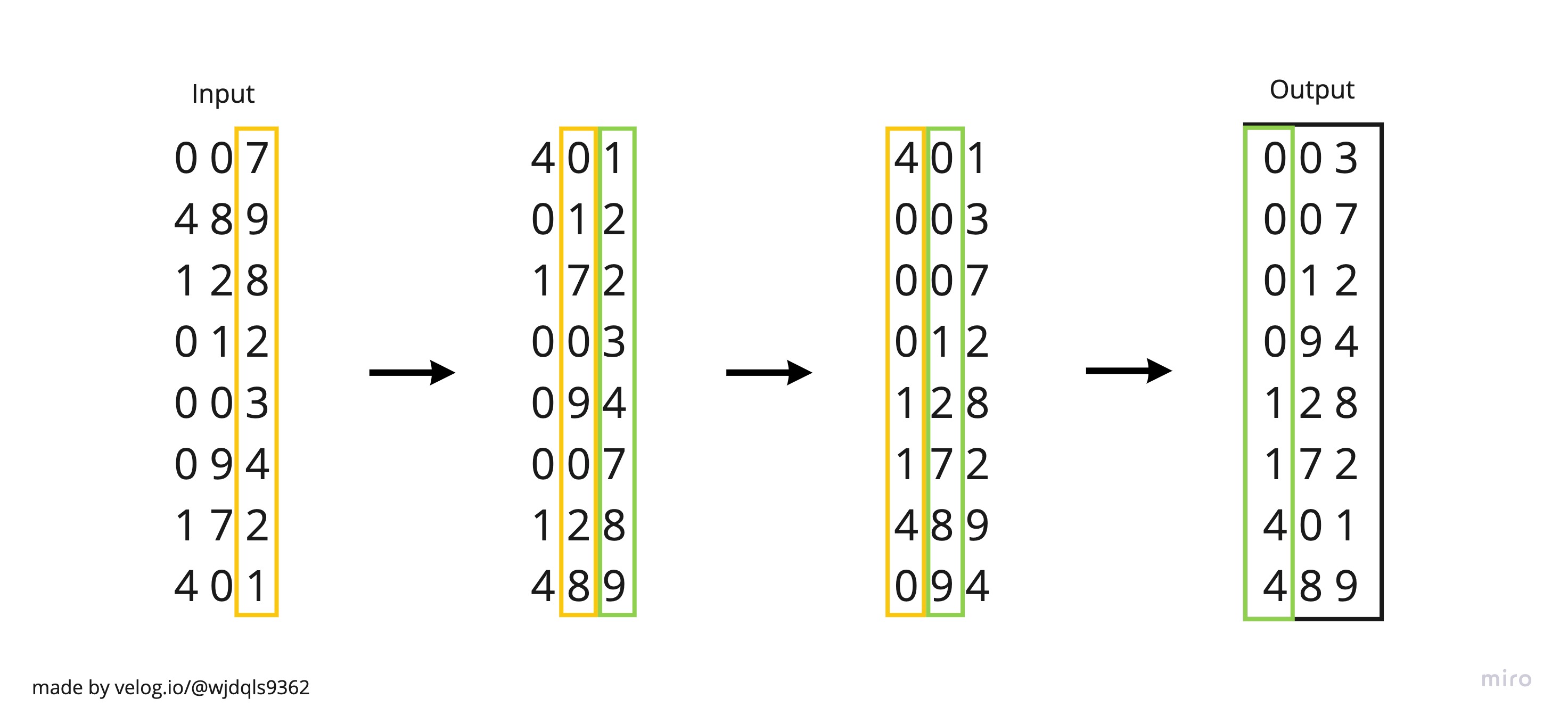
Radix sort(기수 정렬)는 0의 자리, 10의 자리, 100의 자리 ... 1 * (0의 n개) 자리수를 기준으로 정렬하는, 비교 연산을 하지 않는 정렬 기법이다.
(기수 : 주어진 데이터를 구성하는 기본 요소. 2진수는 0과 1, 10진수는 0~9, 영문자는 a~z까지 각 기수의 개수만큼 만드는 것)

O(n)이라는 굉장이 짧은 시간복잡도로, 정렬법들 중 O(NlogN)을 깨는 유일한 정렬법으로, 엄청나게 빠르다.
그러나 데이터 타입이 일정해야 하고, 양의 정수는 양의 정수 끼리 음의 정수는 음의 정수끼리 비교해야 하는 등 구현에 많은 조건이 붙어 사용이 까다롭다. 또한 제자리 정렬이 아니기 때문에 추가적인 메모리 공간이 필요하다.

기수 정렬은 보통 내부적으로 중간 정렬을 사용하는데, k(요소 중 최댓값)에 따라 사용되는 중간 정렬이 다르다.
k가 작을 때는 counting sort(계수 정렬)을, k가 클 때는 quick sort를 사용하는 것이 좋다.

// 양의 정수만 정렬 가능한 로직
function radixSort(arr) {
  const max = Math.max(arr);
  let radix = 1; // 자릿값
  while (parseInt(max / radix) > 0) { // 최댓값이 가지는 자릿수까지만 반복
    arr = countingSort(arr, radix); // radix를 지정해서 인자로 받는 countingSort 함수를 내부적으로 이용
    raidx *= 10;
  }
  return arr;
};