[Algorithm] Bineary Search(O(N)을 O(logN)으로 줄이기)

Intro

O(N) 로직을 O(logN)으로 만드는 Bineary Search 로직에 대해서 학습했다.
오름차순으로 정렬된 두 배열을 하나로 합쳤을 때, 입력받은 k번째 요소를 조회하는 알고리즘에 대해서 이해하게 되었다.

Bineary Search를 이용해서 시간복잡도 줄이기

해당 문제는 두 배열의 요소를 하나 하나 확인하면서 cursor를 움직이는 가장 보통의 O(K)로직이 있지만, 이진 탐색(Bineary Searcgh)를 이용해서 시간복잡도를 O(logK)으로 줄일 수 있다.

조회를 곧 세기(count)라고 생각하고, 총 k번 count를 한다고 생각하자.
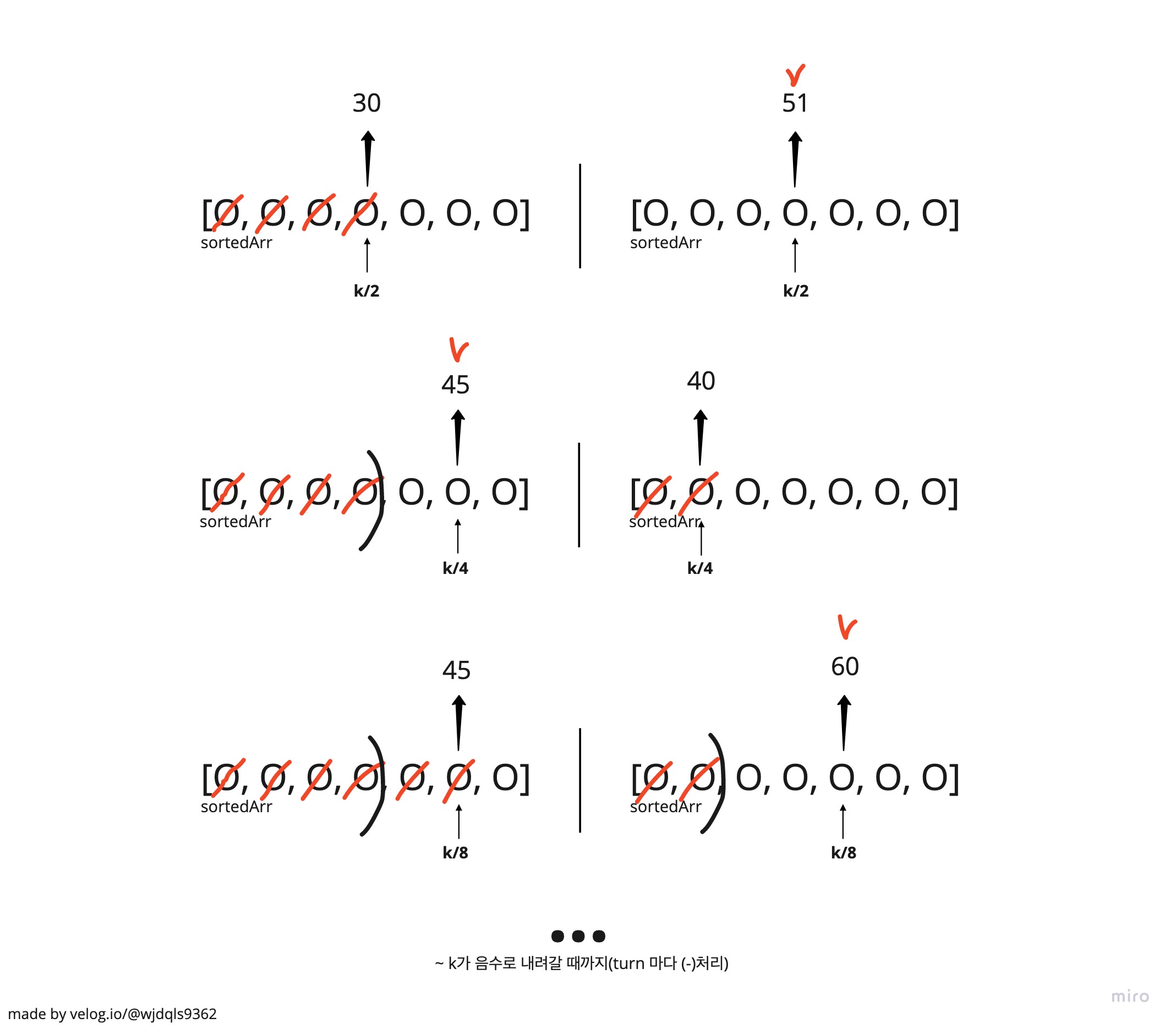
count를 0부터 시작해서 +1씩(~k) 올라가지 않고, k/2를 해서 k의 반값 i에 위치한 요소들 간의 비교를 통해 조회를 진행한다. 로직을 수도코드로 정리한다.

const getItemFromTwoSortedArrays = function (arr1, arr2, k) {
  // k번째 요소를 찾는 것 === 앞에서부터 k번 count했을 때의 요소
  // 이진 탐색법을 이용하기 위해 주어진 두 개의 배열(arr1, arr2)를 합치지 않고, k를 절반으로 나누어 각각의 배열에서 따로 count를 센다.
  
  // while문 : k의 값이 음수가 될 때까지 반복
  // leftStep은 leftArr(arr1)의 count 할당량(k/2), rightStep은 rightArr(arr2)의 count 할당량(k/2)이라고 생각한다.
  
    // 엣지 케이스에 대한 if문
    // 1. 할당된 count가 아직 남았음에도 불구하고 현재 기준(Idx: cursor)이 arr1의 끝에 도달했을 때, 남아있는 k를 rightArr(arr2)에 배분한다.
    // 2. 할당된 count가 아직 남았음에도 불구하고 현재 기준(Idx: cursor)이 arr2의 끝에 도달했을 때, 남아있는 k를 leftArr(arr1)에 배분한다.


    // 엣지 케이스에 대한 if문
    // 1. 현재 남아있는 count보다, 남아있는 요소(arr1.length - leftIdx: 현재 cursor 뒤에 있는, count 후보 요소들)가 적을 경우, leftStep(현재 할당량)을 남아있는 요소들의 개수로 바꿔준다. (앞의 요소는 이미 모두 count 되었고 남아있는 요소는 5개인데, 현재 남아있는 count수가 7개라면, 7개에서 5개으로 바꿔줘야 할 것)
    // 2. 현재 남아있는 count보다, 남아있는 요소(arr2.length - rightIdx: 현재 cursor 뒤에 있는, count 후보 요소들)가 적을 경우, rightStep(현재 할당량)을 남아있는 요소들의 개수로 바꿔준다.

    // 이제 본격적으로 count 탐색문
    // 이진 탐색으로 가기 때문에, 두 배열의 현재 cursor(Idx)에서 현재 진행해야하는 count수(leftStep/rightStep)를 합친 index의 값을 비교한다. (가장 첫 시행 때는, k가 100인 경우 두 배열의 50번째 Idx 값을 비교하게 된다. Idx는 0, Step은 50)
    // 비교 후 그 값이 작은 배열은, 해당 값 앞의 요소에 대해서 다시 검사할 필요가 없다. count에 포함해도 되는, 비교된 큰 값보다 무조건 작은 값이기 때문. 그러므로, 값이 작은 쪽의 배열의 cursor(Idx)를 옮긴다. 다음 turn 부터는 cursor 이후로만 탐색한다.
    // 한 번 처리가 끝나면, k값을 절반으로 떨어트린다. (위의 "count에 포함해도 되는 무조건 작은 값."에 의해서, 후보군에서 떨어진 요소들은 무시하게되는 처리.
    
    // 반대의 경우 오른쪽 배열 arr2의 cursor가 옮겨진다.

  // while문을 끝내고 나왔을 때, 두 개의 배열은 조정된 cursor를 가질 것이고, 해당 값 중 더 큰 값이 k번째 요소일 것이다. (k번째를 벗어나지 않는다.)
};