[JavaScript] TWIL : 자료구조 3/3 Gragh, Tree, Binary Search Tree (20/10.22~10.27)
Data Structure sprint를 마무리했다.
마지막으로 학습한 자료구조는 총 3가지이다.
이번에도 직접 그린 자료구조와 함께.(ㅎㅎ)
1. Gragh
2. Tree
3. Binary Search Tree
1. Gragh
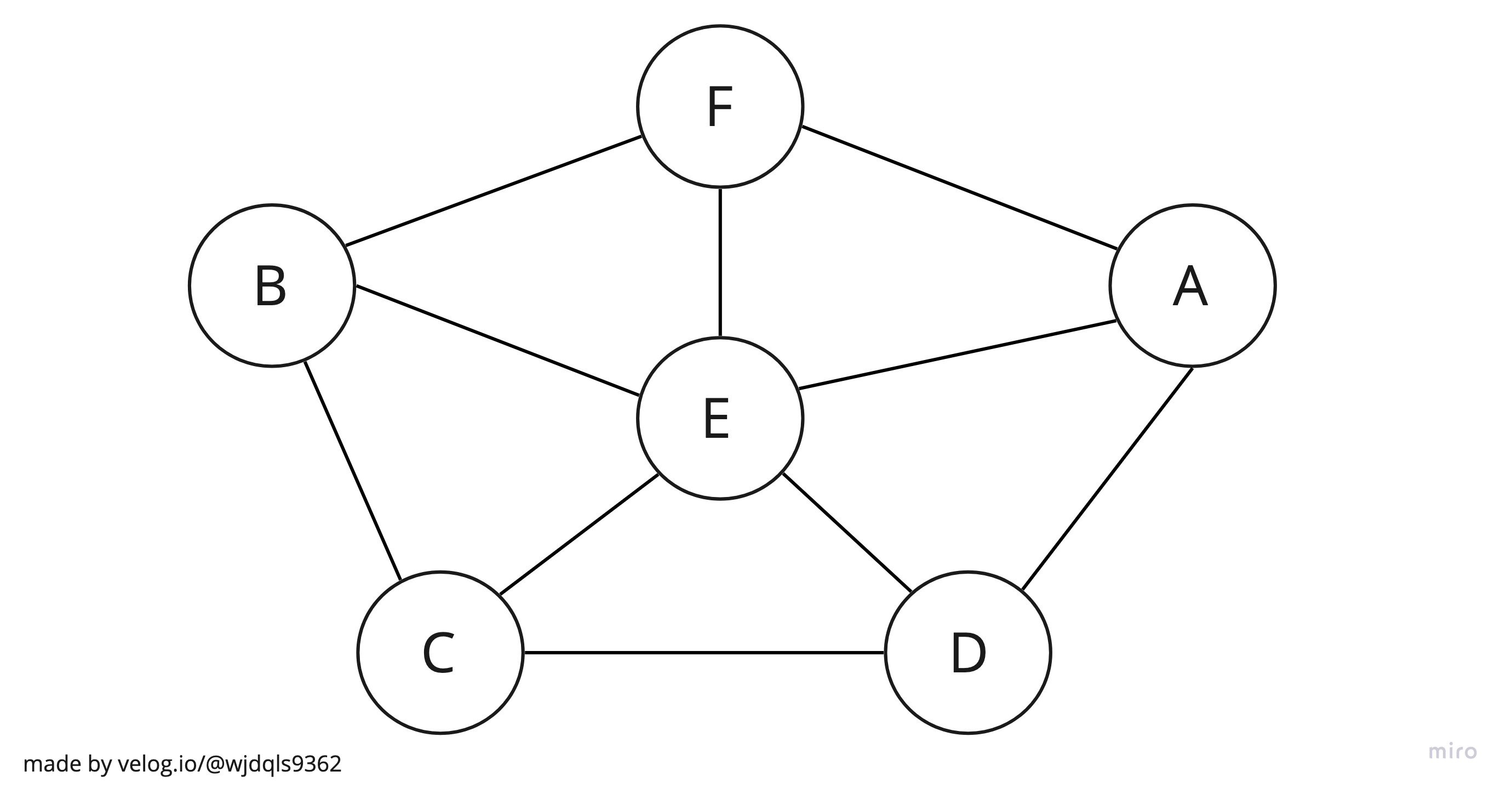
그래프는 노드와 노드 사이를 잇는 간선(edge)로 구성되어 있다. 무방향일수도 있고, 방향이 있을 수도 있다.
구현 방식으로는 인접 행렬방식과 인접리스트 방식 2가지가 있는데,
인접 행렬방식은 n * n으로 이루어져있는 2차원의 배열로 작성하는 방식이다. 간선의 유무가 0과 1로만 이루어져있어 데이터의 변화에 대해 빠르게 대처할 수 있다는 장점과, 그만큼 메모리를 비교적 많이 쓴다는 단점이 있다.
인접 리스트방식은 앞서 배운 linkedList구조처럼 각각의 노드는 연결되어있는 노드의 리스트를 가진다. 메모리를 필요한 만큼만 사용할 수 있는 장점과, 인접 행렬방식보다는 접근성이 비교적 느리다는 단점을 가지고 있다.
실생활에서 정말 많이 쓰이는 자료구조이다. 대표적으로 지도, 네비게이션, sns 팔로우 네트워크 등이 있다고 할 수 있겠다.
// 위의 그림에 대한 두 가지 구현 방식
// 1. 인접 행렬 방식 // 2. 인접 리스트 방식
// A B C D E F A => D-E-F
// A 0 0 0 1 1 1 B => C-E-F
// B 0 0 1 0 1 1 C => B-D-E
// C 0 1 0 1 1 0 D => A-C-E
// D 1 0 1 0 1 0 E => A-B-C-D-F
// E 1 1 1 1 0 1 F => A-B-E
// F 1 1 0 0 1 0 (위 세로의 A,B,C,D,E,F도 연결상태!)나는 이번에 무방향 그래프를 인접 리스트방식으로 구현했다. 속성과 method를 살펴보자.
Property
- 저장공간인 nodes(빈 객체)
Method
- data를 삽입하는 addNode(node)
- data의 존재여부를 확인하는 contains(node)
- data를 삭제하는 removeNode(node)
- data간 연결여부를 확인하는 hasEdge(fromNode, toNode)
- data를 연결하는 addEdge(fromNode, toNode)
- data간 연결을 제거하는 removeEdge(fromNode, toNode)
- 그 외에는 구현정도에 따른다.
Psuedo Code
addNode(node) {
// nodes에 node를 추가하고, 다른 노드와 연결 시 data를 추가할 빈 배열을 함께 넣어줌
}
contains(node) {
// nodes의 key만 뽑아 node값을 includes하는지를 true/false로 반환
}
removeNode(node) {
// 1. 해당 node의 키값쌍을 삭제
// 2. 객체를 순회하며 다른 node들에 있는 해당 node값을 삭제
}
hasEdge(fromNode, toNode) {
// fromNode와 toNode가 서로의 값을 가지로 있는지 검사 후 true/false 반환
}
addEdge(fromNode, toNode) {
// fromNode, toNode 서로의 값에 서로를 추가
}
removeEdge(fromNode, toNode) {
// 1. fromNode에서 toNode를 찾아 삭제
// 2. toNode에서 fromNode를 찾아 삭제
}2. Tree
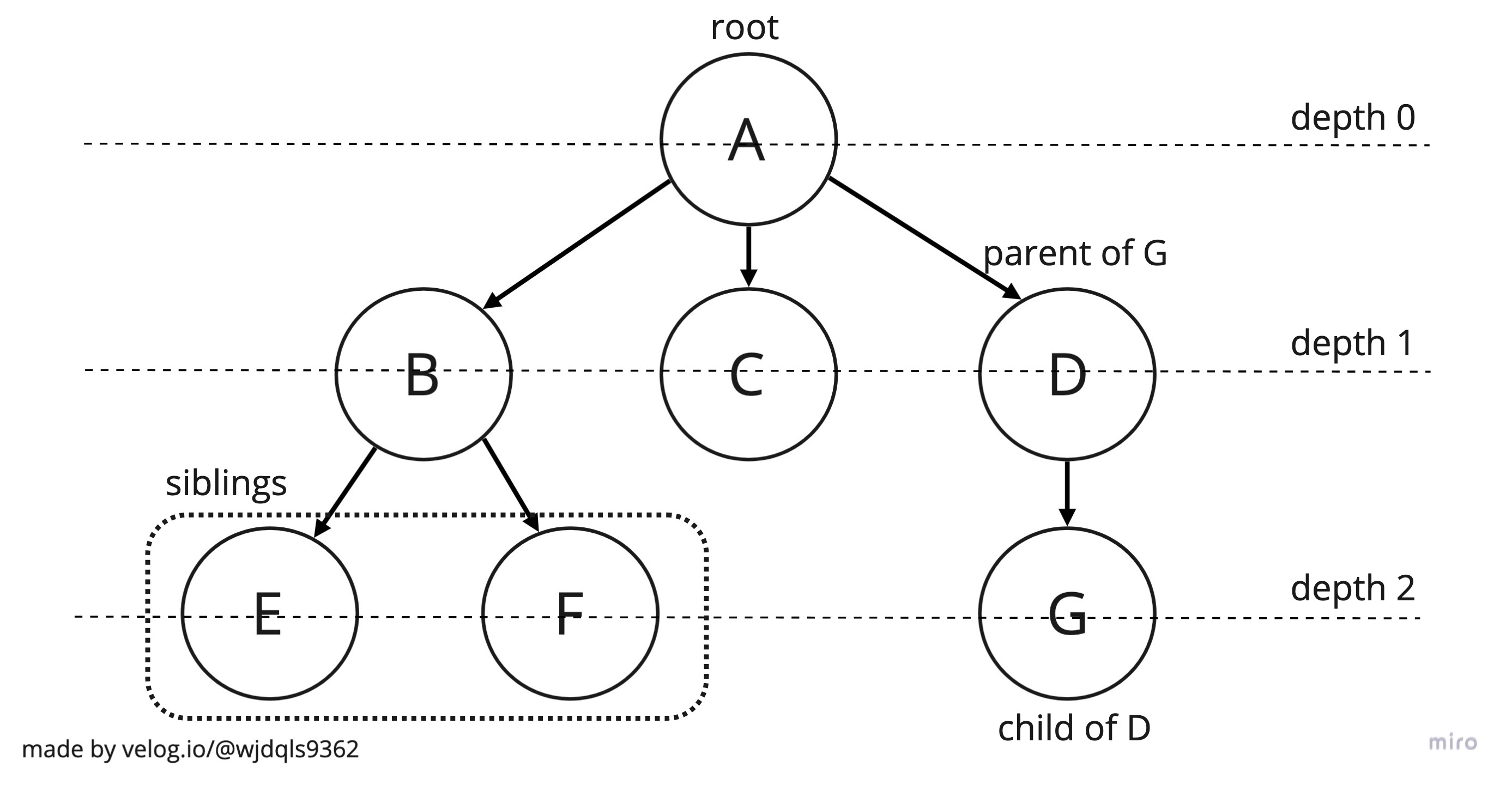
Tree는 로 node로 구성된 계층이 확실하게 나뉘어있는 자료구조이다. 최상위 노드(root)를 만들고, 루트 노드의 child를 추가하고, 그 child에 또 child를 추가하는 방식으로 구현할 수 있다. 부모 자식 관계가 확실하기 때문에 재귀적인 구조이다.
Tree도 정말 실생활에서 많이 쓰이는 자료구조이다. DOM부터 시작해서, 자동완성 기능/검색 말고도 Tree로부터 파생된 많은 응용Tree 구조가 있다.
Property
- data가 저장되는 value
- 자식 data를 담을 수 있는 children
Method
- root의 child로 data를 추가하는 insertNode(value)
- 해당 value(data)의 존재여부를 확인하는 contains(value)
- 그 외에는 구현 정도에 따른다.
Psuedo Code
insertNode(value) {
// 1. children에 새로운 treeNode instance 추가
// 2. 추가한 node에 value 추가
}
contains(value) {
// 1.children을 조회해 해당 value가 있는지 검사하는 함수 하나 만들기 (재귀)
// 2. 찾으면 true를 반환 (탈출)
// 2-1. value를 찾지 못하고 chilren이 존재하면 재귀
}3. Binary Search Tree
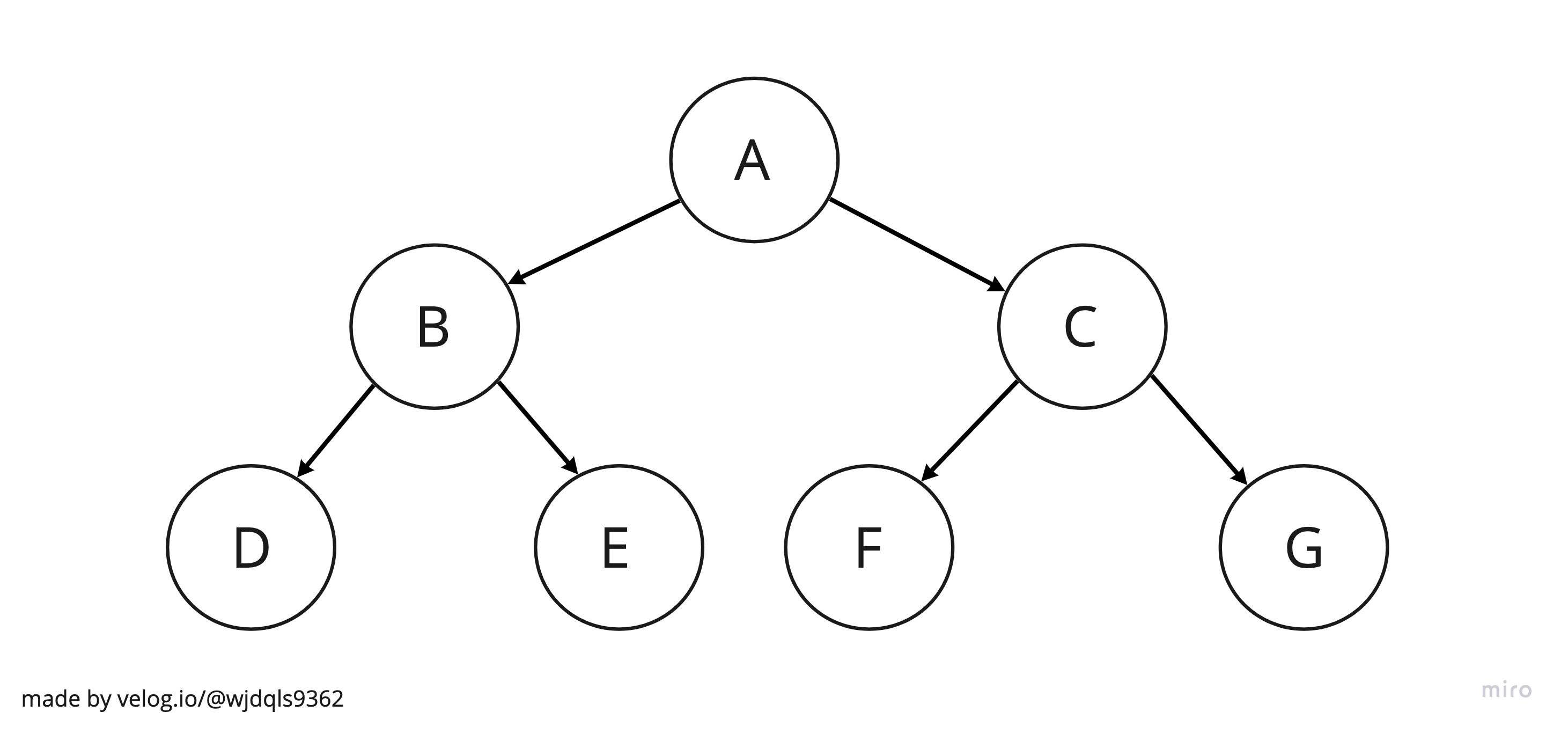
Binary Search Tree는(이진 탐색 트리:이하 BST) Tree에서 파생된 구조이다. root를 포함 모든 node가 자식을 2개까지만 가질 수 있다.
자식이 정렬되는 방법도 정해져 있다. 부모보다 작은 값은 왼쪽에, 큰 값은 오른쪽에 정렬된다.
이런 특성 때문에, BST는 tree의 기본 탐색 시간 복잡도인 O(n)보다 더 적은 O(logN)을 가진다. 시간 복잡도는 후에 따로 블로깅 해야 할 것이다.
실생활 예제는 앞서 말했듯이, 탐색 시간복잡도가 O(n)보다 훨씬 적은 O(logN)이므로 검색을 주 기능으로하는 언어사전 같은 DB에 많이 쓰인다.
BST는 순회 방법이 3가지가 존재한다. (그림 참조)
- 전위순회 : 부모 > 왼쪽 > 오른쪽 ( A > B > D > E > C > F > G )
- 중위순회 : 왼쪽 > 부모 > 오른쪽 ( D > B > E > A > F > C > G )
- 후위순회 : 왼쪽 > 오른쪽 > 부모 ( D > E > B > F > G > C > A )
이번 sprint에서는 중위순회를 구현해보았다.
Property
- data를 저장하는 value
- 왼쪽 자식 left
- 오른쪽 자식 right
Method
- data를 삽입하는 insert(value)
- data의 존재여부를 검사하는 contains(value)
- 중위순회 inorder(callback)
- 그 외에는 구현정도를 따른다.
Psuedo Code
insert(value) {
// 1. value와 root부터 비교시작
// 2. root보다 작다면, ( left가 비어있으면 value 할당(탈출), 비어있지 않으면 재귀 )
// 3. root보다 크다면, ( right가 비어있으면 value 할당(탈출), 비어있지 않으면 재귀 )
}
contains(value) {
// 1. value가 일치하면 true 리턴 (탈출)
// 2. left가 null일 때까지 재귀
// 3. right가 null일 때까지 재귀
}
inorder(callback) {
// 중위순회 : 왼 > 부모 > 오
// 1. left가 null일 때까지 재귀
// 2. callback(this.value)
// 3. right가 null일 때까지 재귀
}이로써 data structure sprint의 대장정이 마무리되었다. 짧은 시간동안 너무나 많은 학습을 해야했었어서 숨이 차긴 했지만, 개발자에게 꼭 필요한 개념이니 부족한 부분은 코스 수료 후 꼭 다시 꼼꼼하게 공부하는 것이 좋다는 엔지니어님들의 말씀이 있었다. 코딩 테스트를 할 때 많이 쓰이는 개념이니 꼭 다시 공부해야할 것ㅠㅠ 지금까지 공부한거라도, 민철 엔지니어님의 1137 복습주기를 이용해서 잊지 말아야할 것....!!!!!!

