💡문제
N×M크기의 배열로 표현되는 미로가 있다.
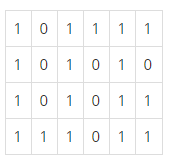
미로에서 1은 이동할 수 있는 칸을 나타내고, 0은 이동할 수 없는 칸을 나타낸다. 이러한 미로가 주어졌을 때, (1, 1)에서 출발하여 (N, M)의 위치로 이동할 때 지나야 하는 최소의 칸 수를 구하는 프로그램을 작성하시오. 한 칸에서 다른 칸으로 이동할 때, 서로 인접한 칸으로만 이동할 수 있다.
위의 예에서는 15칸을 지나야 (N, M)의 위치로 이동할 수 있다. 칸을 셀 때에는 시작 위치와 도착 위치도 포함한다.
입력
첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.
출력
첫째 줄에 지나야 하는 최소의 칸 수를 출력한다. 항상 도착위치로 이동할 수 있는 경우만 입력으로 주어진다.
예제입력
4 6
101111
101010
101011
111011예제출력
15📖내가 작성한 code
from collections import deque
n,m=map(int,input().split())
maze=[list(map(int,input())) for _ in range(n)]
dx=[-1,0,1,0]
dy=[0,-1,0,1]
dq=deque()
def BFS(x,y):
dq.append((x,y))
while dq:
p,q=dq.popleft()
for i in range(4):
nx=p+dx[i]
ny=q+dy[i]
if nx<0 or nx>=n or ny<0 or ny>=m:
continue
if maze[nx][ny]==1:
maze[nx][ny]=maze[p][q]+1
dq.append((nx,ny))
BFS(0,0)
print(maze[n-1][m-1])

