저번 최적화 포스팅에 이어 이번에는 quadratic program을 정리해보려고 한다.

최적화의 모든 부분을 정리하고 싶지만 현실적으로 시간이 부족할 것 같아 앞으로도 지금처럼 주제별로 포스팅을 할 예정이고, 본 내용이 이 글을 읽는 분들에게 도움이 되었으면 좋겠다.

본문에서 다룰 내용은 다음의 세 가지 이다.

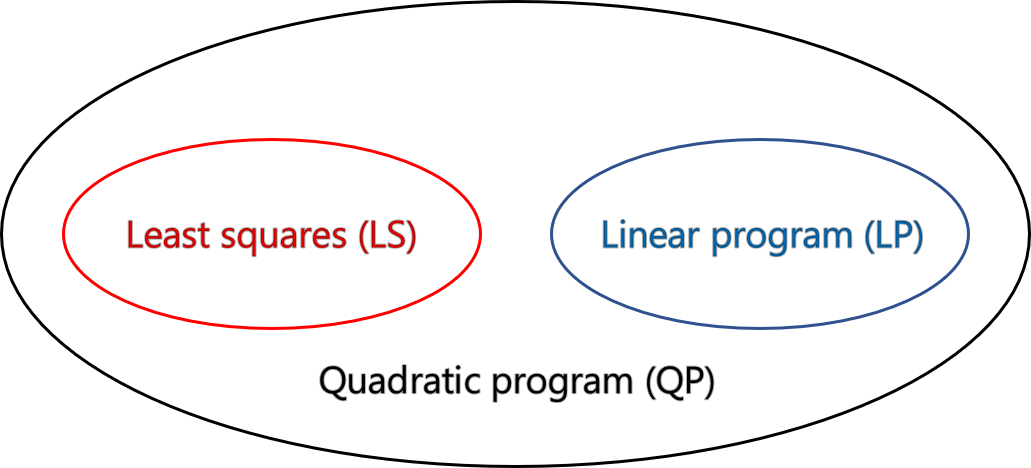
1. QP는 무엇이고, LP와 LS가 QP의 special case 인지

2. QP가 closed-form solution을 가지는 special case: constrained LS에 대하여

3. General QP는 어떤 식으로 다룰 것인지

Quadratic program

QP in standard form

먼저 QP의 standard form은 다음과 같다.

이때, $Q = Q^{\intercal} \in \mathbf{R}^{d \times d} \succeq 0$ 은 positive semi-definite (PSD) matrix 이다.

Square & symmetric matrix $\left( \textrm{i.e., }Q = Q^{\intercal} \in \mathbf{R}^{d \times d} \right)$ is positive semi-definite, if $v^{\intercal} Q v \geq 0, \forall v \in \mathbf{R}^d. \left( \textrm{i.e., all the eigenvalues of } Q \textrm{ are non-negative} \right)$
$\Rightarrow$ Simply denoted by $Q \succeq 0$. $\left( \succeq: \textrm{ curly inequality, which means that all the eigenvalues are non-negative.} \right)$
$\rightarrow$ 부등호와는 다른 개념인데, 다음의 링크를 참고하자.

참고로 matrix의 부호가 positive 하다는 것은 eigenvalue 가 positive 하다는 것과 동일하다.

이제 이 problem이 convex가 맞는지 알아보자. 먼저 inequality 및 equality constraint에 의해 유도되는 set은 convex 임이 자명하다. 이제 objective function에 대해 생각해보자.

첫 번째 항 $w^{\intercal}x$ 은 affine 이므로 convex 이다. 또한 convexity는 additivity에 대해 유지된다. 따라서 우리는 두 번째 항 $x^{\intercal} Q x$ 에 대해서만 판단해주면 된다.

Second order condition of convexity 에 의해, 우리는 objective function의 Hessian 즉, second derivative가 PSD 라면 이는 convex 임을 알 수 있다.

이제 QP가 LP와 LS를 포함하는 관계인지 알아보자.

Subsumes LP

$Q=0$ 인 상황을 생각해보자.

이는 LP와 같다.

Subsumes LS

LS의 standard form을 생각해보면 다음과 같다.

이때 objective function을 변형하여 (massage), QP form으로 만들어보자.

먼저 $b^{\intercal}b$ 은 optimization variable $x$에 영향을 받지 않는 constant이기 때문에 중요하지 않다. 두 번째 term $- 2b^{\intercal}Ax$ 은 x에 대해 affine 이므로, QP의 $w^{\intercal}x$ 에 대응된다. 마지막으로 첫 번째 term은 $x^{\intercal}Qx$ 와 대응하는 것을 알 수 있는데, 이때 $A^{\intercal}A$ 가 $Q$ 와 대응하므로 우리는 $A^{\intercal}A$가 PSD 임을 보이면 된다.

$A^{\intercal}A \succeq 0$ 의 증명:
$v \in \mathbf{R}^d$ 인 어떤 vector $v$ 를 생각해보자.
이때, $v^{\intercal}A^{\intercal} A v = (Av)^{\intercal} Av$ 이다.
$(Av)^{\intercal} Av$ 는 $Av$의 inner product 이므로, $(Av)^{\intercal} Av = \vert \vert Av\vert \vert^2$. 이는 Euclidean distance 이므로 non-negative 하다. (PSD 임을 만족)
위의 관계는 $\forall v \in \mathbf{R}^d$ 에 대해 성립한다.

Equality-constrained LS

이제 closed-form solution이 존재하는 QP에 대해 알아보자: Equality-constrained LS
(기존의 LS와 다른 점은 equality constraint 가 추가되었다는 점)

여기서 $A$의 dimension을 생각해보자. 우리는 $m \geq d$ 인 상황에만 관심이 있다.
(만약 $m < d$ 이면 under-determined system 이므로 in general, infinite solution 존재 $\rightarrow$ Objective function을 0으로 만들기 쉽다.)

이제 $C$를 보자. 이는 $p$와 $d$의 관계에 따라 두 가지 case로 나눠진다.

1. $p \geq d$
   이는 interesting case가 아니다. 이 경우에는 equality constraint에 의해 $x^*$ 가 쉽게 결정 되거나 근이 없게 된다.
   $p=d$ 인 경우를 생각해보면, 미지수와 식의 개수가 같은 경우이므로 이때의 근은 하나로 결정된다. 따라서 objective function의 값도 결정되기 때문에 이 case 에서는 특별히 얻을 수 있는 것이 없다.
   $p > d$ 인 경우, 주어진 변수에 대한 constraint가 매우 많다는 것이다. 이때는 가지고 있는 변수가 더 적기 때문에 no solution case가 된다.

2. $p < d$
   앞서 설명했던 이유로 인해, 본 case가 interesting 하다.

참고로 $b \in \mathbf{R}^m$, $e \in \mathbf{R}^p$ 이다. 이를 정리해보면 다음과 같다.

이제 두 가지 가정 을 할 것이다.
(wide matrix: 행보다 열이 더 많은 가로로 큰 행렬, tall은 세로로 긴 행렬)

• $\textrm{rank}(C) = p$ $\rightarrow$ fat matrix, row 끼리 linearly independent, full rank.

• $\textrm{rank} \left( \begin{bmatrix} A\\ C\\ \end{bmatrix} \right) = d$ $\rightarrow$ tall matrix, column 끼리 linearly independent, full rank.

이 조건들은 보통 실제로 성립하기도 한다.

Closed-form solution

이제, 위에서 정리한 조건들을 다 적어 새로 식을 작성해보자.

이때의 closed-form solution을 먼저 표현해 볼 것인데, 이에 앞서 일반적인 LS problem에서의 closed-form solution을 다시 복습해보자.

이를 다음과 같이 변형해볼 수 있다.

행렬 곱으로 정리하면 다음과 같다.

(아마 맨 왼쪽 행렬 중 첫 열에 대해서는 이해했을 것이다. $C^{\intercal}$ 와 0으로 구성되어 있는 두 번째 열은 non-trivial 하기 때문에 일단 받아들이고 넘어가자. $z$는 어떠한 vector 이다.)

여기서 $x^*$ 는 다음과 같이 구할 수 있다. 참고로, '$d\textrm{ - Components}(\cdot)$: takes the first $d$ components of $(\cdot)$' 이다. 즉 여기서는 $(d+p)$ 차원 vector 에서 처음 $d$ 개의 성분만 얻는 것을 뜻한다.

Closed-form을 조건 식에서 바로 유도하는 것은 어려우니, $x^*$ 가 위의 조건을 만족하면 optimal 함을 보이는 방식으로 증명을 진행할 것이다.

한편, 증명에 앞서서 정리하고 넘어가야 할 식이 있다.

위의 equation을 KKT equation 이라고 한다. 그리고 가장 왼쪽의 matrix를 KKT (Karush-Kuhn-Tucker) matrix 라고 한다. (이후 다룰 KKT conditions 와 관련있다.)

다시 증명으로 돌아오면 우리에게 필요한 증명은 두 가지 이다. 각각을 증명해보자.

1. If $\textrm{ } \exist (x^*,z) \in \mathbf{R}^{d+p}$ s.t. $(*)$, then $x^*$ must be the optimal solution.
   i.e., $\vert\vert Ax-b \vert\vert^2 \geq \vert\vert Ax^*-b \vert\vert^2$, $\forall x$ subject to $Cx-e = 0.$

이제 $(**)$ 를 증명하자.

$(***)$이 성립하는 이유는 $(*)$ 에서 $2A^{\intercal}Ax^{*} - 2A^{\intercal}b = -C^{\intercal}z$ 가 성립하기 때문이다.

2. $\begin{bmatrix} 2A^{\intercal}A&C^{\intercal}\\ C&0\\ \end{bmatrix}$ is invertible

이는 귀류법을 통해 증명할 것이다: 만약 invertible 하지 않다고 가정해보자.

Not invertible 이라는 말은 곧 full-rank가 아니라는 것과 같다. 또한 주어진 행렬의 차원은 $(d+p) \times (d+p)$ 이다. 여기서는 invertible 하지 않음을 가정했으므로 어떠한 column은 다른 column들을 통해 표현될 수 있다. (linearly dependent)

따라서 다음의 식이 성립한다.

이를 풀어보면,

앞서 우리는 $\begin{bmatrix} A \\ C \end{bmatrix}$가 full-rank 임을 가정했다. 따라서 $\bar{x}=0$ 이다.

이를 앞선 관계식에 적용해보면, $C^{\intercal}\bar{z} = 0$ 이다. 그런데 이 역시 앞선 가정에 의해 $C^{\intercal}$의 column들이 linearly independent 하므로, $\bar{z} = 0$ 이다.

정리하면 $\bar{x}=\bar{z}=0$, 이는 처음 가정에 모순된다.

General QP

초반에 언급했던 바와 같이, 일반적으로 QP는 다음과 같은 standard form을 가진다.

그렇다면 QP의 general solution은 무엇일까? 아쉽게도 QP의 general solution은 존재하지 않는다. 이는 추후 strong duality 를 다룰 때, 더 논의해보도록 하자.

Reference

카이스트 서창호 교수님 강의 - EE424: 최적화개론 lecture 10.

KKT condition을 잘 정리한 한글 블로그