이번 포스팅에서는 semi-definite program (SDP)에 대해 알아보자.

여기서 다룰 내용은 크게 세 가지 이다.

1. SDP가 무엇이고, 이는 convex problem이 맞는지
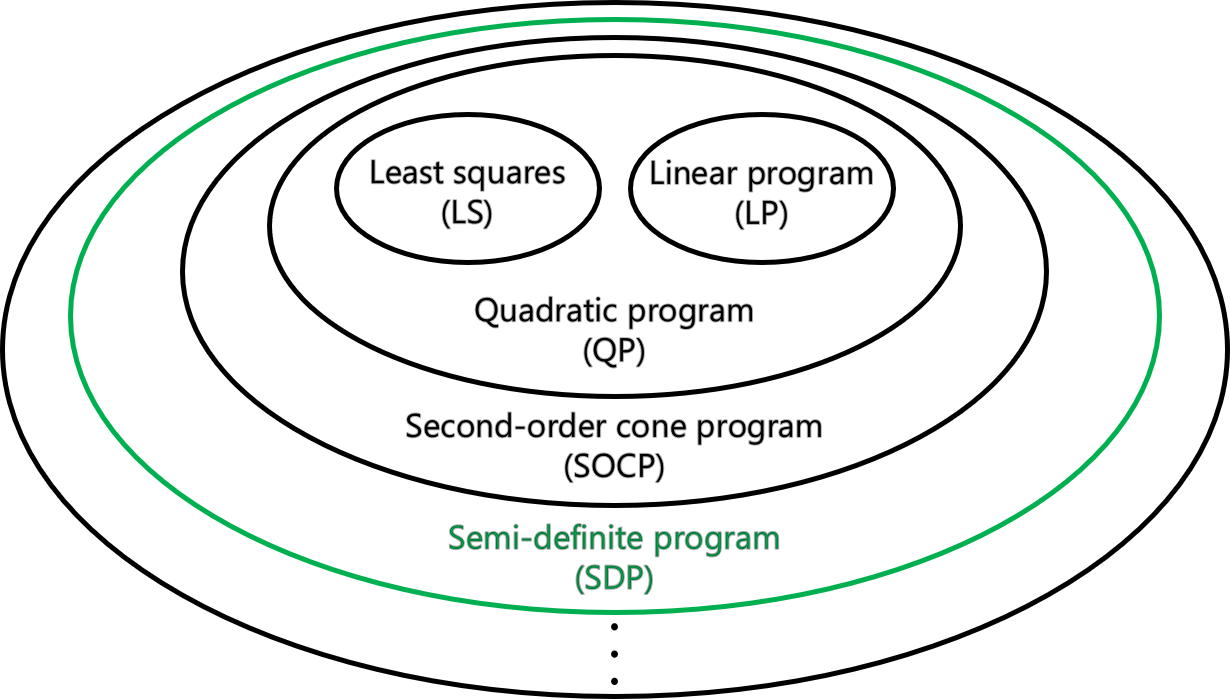
2. SDP가 LP, LS, QP, SOCP를 포함하는 개념이 맞는지
3. Schur complement lemma란 무엇인지

Semi-definite program (SDP)

Standard form

먼저, SDP의 standard form은 아래와 같다.

참고로 $G$ 와 $F_i$ 는 symmetric matrices 이다. 여기서 주목할 점은 inequality constraint 인데, 식을 보면 여러개의 행렬이 $x:=(x_1,x_2,\cdots,x_d)$의 성분들과 linear 하게 연산되어 있는 것을 알 수 있다. 따라서 이를 Linear matrix inequality 즉, LMI 라고 부른다.

Convexity

다음으로 SDP의 convexity를 증명해보자. Standard form을 보면 $w^{\intercal}x$ 와 $Cx=e$는 모두 affine 이므로, 우리는 inequality constraint에 의해 유도되는 set $S$가 convex 임을 보이기만 하면 된다.

증명은 $x, y\in S$ 와 $\lambda \in [0,1]$에 대한 convex combination $\lambda x + (1-\lambda) y$가 $S$ 안에 있는지 확인하는 방식으로 할 수 있다.

즉, '$x, y \in S$' 라는 가정과 'PSD matrix 2개의 convex combination 또한 PSD' 라는 사실로 인해 $S$ 는 convex set 이다.
$\Rightarrow$ 따라서, SDP는 convex problem 이다.

참고로, 두 PSD의 convex combination이 PSD 인 이유는 다음과 같다.
Proof: Let $A, B \in \mathbf{R}^{m\times m} \succeq 0$ and $v \in \mathbf{R}^m \Rightarrow \lambda A + (1-\lambda) B \succeq 0 \textrm{ ?}$
$\lambda A + (1-\lambda) B$ 의 양 옆에 $v$를 곱하면 다음과 같다.
$v^{\intercal} (\lambda A + (1-\lambda) B) v = \lambda v^{\intercal} A v + (1-\lambda)v^{\intercal} B v \succeq 0 \quad (\because A,B \succeq 0, \lambda \in [0,1])$

Relation with other methods

이제 SDP가 다른 방법들을 포함할 수 있는지 알아보자. 이에 앞서 SDP의 standard form을 다시 remind 해보면 다음과 같다.

편의를 위해 위의 식을 $(*)$ 로 하자.

LP

$(*)$ 에서 $G$ 와 $F_i$ 를 diagonal matrix (대각 행렬) 이라 하자. 그렇다면 우리는 식을 아래와 같이 표현할 수 있다.

이때 $[A]_{ii}$ 는 $A$의 $(i,i)$ 성분을 의미한다.

여기서 우리는 diagonal PSD가 non-negative 한 성분들로 이루어진다는 성질을 이용했다. 즉 위의 과정을 통해 우리는 LP가 SDP의 특정 case 임을 알 수 있다. (LP의 inequality constraints로 바뀌었기 때문이다.)

LS and QP

LS와 QP에 대한 포함 관계를 보이는 것은 SOCP를 보이는 것만큼이나 어렵다. (포스팅에서 다루지는 못했지만) 앞선 강의에서 SOCP가 LS 및 QP를 포함한다는 것을 보였기 때문에, 여기서는 SDP가 SOCP를 포함하는지에 초점을 맞춰볼 것이다. (이를 보이면 LS와 QP도 SDP에 포함된다는 것이기 때문)

SOCP

SOCP의 standard form을 생각해보자.

우리가 보여야 할 것은 SOC constraint에서 LMI로의 변환이 항상 가능하다는 것이다. 위의 식에서 SOC constraint를 다음의 형태로 바꿔보자.
(To be feasible $\rightarrow c^{\intercal}_i x + e_i \geq 0$)

(Remind LMI: $G + x_1F_1 + \cdots + x_dF_d \succeq 0$)

여기서 WLOG (without loss of generality), $c^{\intercal}_i x + e_i >0$ 라 둘 수 있다. 만약 $c^{\intercal}_i x + e_i=0$ 이면 $A_ix-b_i =0$ 인데, 이때 두 식은 $Fx = g$ (equality constraint)에 합쳐질 수 있고, 이는 LP와 같기 때문이다.

이제 식을 마저 정리해보자. $c_i^{\intercal}x + e_i >0$ 이므로, 이를 양변에 나누면 다음과 같다.

$(**)$는 아래와 같이 표현할 수 있다. $(I_{k_i \times k_i}: k_i \times k_i \textrm{ identity matrix})$

이때, 위의 식에서 좌변을 행렬 $(c_i^{\intercal}x + e_i) I_{k_i \times k_i}$의 Schur complement 라고 한다. Formal 한 definition은 아래와 같다.

Schur complement

Definition: Suppose that $p$ and $q$ are non-negative integers. And $A\in\mathbf{R}^{p\times p}, B\in\mathbf{R}^{p\times q}, C\in\mathbf{R}^{q\times q}$.
Let $X := \begin{bmatrix} A&B\\ B^{\intercal}&C\\ \end{bmatrix} \in \mathbf{R}^{(p+q) \times (p+q)}$. Then if $A$ is invertible, the Schur complement $S$ of the block $A$ in matrix $X$ is defined as $S := C-B^{\intercal}A^{-1}B.$

이제 정의를 알았으니 앞선 계산식에 대응시켜보면, formal definition을 기준으로 $C=c_i^{\intercal}x + e_i$, $B=A_ix-b_i$ 그리고 $A=(c_i^{\intercal}x + e_i) I_{k_i \times k_i}$ 인 상황임을 알 수 있다.

한편 Schur complement와 관련된 매우 유명한 lemma를 하나 사용하면, 우리는 SDP의 standard form에 있는 inequality constraints를 유도해낼 수 있다. 해당 lemma는 다음과 같다: Schur complement lemma

Schur complement lemma
Suppose $A \in \mathbf{R}^{p \times p} \succ 0$ and $C$ is symmetric. Then,
$X := \begin{bmatrix} A&B\\ B^{\intercal}&C\\ \end{bmatrix} \succeq 0 \Leftrightarrow S:= C-B^{\intercal}A^{-1}B \succeq 0$

이제 앞서 대응시킨 변수들을 대입하면, SOC constraint를 다음의 형태로 바꿀 수 있다.

여기서 $F_{i}(x) \in \mathbf{R}^{(k_i+1) \times (k_i+1)}$ 는 symmetric 이고 PSD이며, 각 원소들은 $x$에 대해 affine 이다. 그렇다면 이는 LMI 일까? 이에 대한 대답은 Yes 이다. 증명은 다음과 같다.

Proof: (Subscript index $i$는 생략)
$F(x) := \begin{bmatrix} (c^{\intercal}x+e) I_{k \times k}& Ax-b \\ (Ax-b)^{\intercal}&c^{\intercal}x+e\\ \end{bmatrix} \succeq 0$ is an LMI?
(LMI: $G + x_1F_1 + \cdots + x_dF_d \succeq 0$)

LMI는 $x$와 관련이 있느냐 없느냐에 따라 크게 두 부분으로 나눠볼 수 있다. (e.g., 행렬 $G$는 $x$ 와 관련이 없는 부분)

따라서 $F(x)$도 두 부분으로 나눠보면 다음과 같이 전개할 수 있다.

이때 $G=\begin{bmatrix} e I_{k \times k}& -b \\ -b^{\intercal}&e\\ \end{bmatrix}$ 임을 알 수 있고, 이는 symmetric 이다.

다음으로 남은 한 부분을 보자. 이는 $x$에 대한 함수인데, 우리의 목적은 이를 $\sum^d_{i=1} x_iF_i$ 꼴로 표현하는 것이다.

각각을 보면 먼저 $c^{\intercal}x$ 는 $\sum^d_{i=1} c_ix_i$ 로 표현할 수 있다. 다음으로 $Ax$는 $\sum^d_{i=1} \square$ 의 형태로 어떻게 표현할 수 있을까.

현재 $A$의 크기는 $\mathbf{R}^{k \times d}$ 이므로 column은 총 $d$ 개다. 각 column을 $a_i \in \mathbf{R}^{k}$ 로 두면 $A$는 $[a_1, a_2, \cdots,a_d]$ 로 나타낼 수 있고, $Ax=\sum^d_{i=1} a_ix_i$ 와 같다. 마찬가지로 나머지 원소에 대해서도 같은 방식을 적용하면, $x_i$는 scalar 값이므로 transpose에 영향을 받지 않기 때문에 다음과 같이 표현할 수 있다.

우리는 마지막 식에서 $\begin{bmatrix} c_iI_{k \times k}& a_i \\ a^{\intercal}_i& c_i\\ \end{bmatrix}$ 를 $F_i$ 로 볼 수 있다. 그렇다면 마지막으로 확인할 것은 $F_i$의 symmetric 여부인데, 행렬 꼴을 보았을 때 이는 symmetric 이다.

따라서 $F(x) := \begin{bmatrix} (c^{\intercal}x+e) I_{k \times k}& Ax-b \\ (Ax-b)^{\intercal}&c^{\intercal}x+e\\ \end{bmatrix} \succeq 0$ 는 LMI 이다.

(Remind SOCP)

지금까지 우리는 $F_i(x) \succeq 0$ 이 LMI 라는 것을 확인했다. 그런데 생각해보면 SOCP에서 $i$ 의 범위는 $1 \leq i \leq m$ 이기 때문에, SDP에서 하나의 LMI를 다뤘던 것과는 달리 여기서는 총 $m$ 개의 multiple LMIs 를 다룬다.

따라서 SDP의 form을 맞춰주기 위해서는 multiple LMIs를 single LMI로 바꾸는 추가적인 연산이 필요하다.

각각의 LMI를 보자. $F_1(x) \succeq 0$ 이고, $F_2(x) \succeq 0, \cdots, F_m(x) \succeq 0$ 이다. 그렇다면 우리는 다음의 large matrix를 생각해볼 수 있다.

한편, 위의 행렬에 대해 다음과 같은 관계식이 성립한다. 증명은 PSD의 definition을 통해 쉽게 할 수 있다.

참고로 $(***)$ 은 symmetric 이기 때문에 $G + \sum_{i=1}^d x_iF_i$ 의 형식으로 표현할 수 있고, 또한 $(***)$ 은 PSD 이므로 이는 LMI 이다.

SDP:

Proof of Schur complement lemma

Schur complement lemma
Suppose $A\succ0$ (PD) and $C$ is symmetric. Then,
$X = \begin{bmatrix} A&B\\ B^{\intercal}&C\\ \end{bmatrix} \succeq 0 \Leftrightarrow S:= C-B^{\intercal}A^{-1}B \succeq 0$
($S$ 는 block $A$ 의 Schur complement)

$\left( \Rightarrow \right)$

다음과 같은 $f(x,y)$를 생각해보자. $(\rightarrow x\in \mathbf{R}^p, y\in \mathbf{R}^q)$

여기서 $f(x,y)$ 는 $x$ 에 대한 2차식인 것을 알 수 있다. 가정에 의하면 $A$ 는 PD 이고, 따라서 $A$는 invertible 하다. (또한 $A$의 모든 eigen-value가 strictly positive)

그렇다면 $f(x,y)$ 는 $x$ 에 대한 convex function 이다. 왜냐하면 $A$ 가 symmetric 하고 PD 이기 때문이다. (엄밀히 말하면, PSD가 아닌 PD 이므로 strictly convex in $x$)

이제 아래와 같이 $g(y)$ 를 설정하고, 그에 해당하는 $x$ 값 (stationary point)를 넣어 전개해보자.

정리하면, $X$는 PSD 이다. PSD의 정의를 생각해보면, 모든 $(x,y)$ 에 대해 $f(x,y) = \begin{bmatrix} x^{\intercal}&y^{\intercal} \end{bmatrix} \begin{bmatrix} A&B\\ B^{\intercal}&C\\ \end{bmatrix} \begin{bmatrix} x \\ y \\ \end{bmatrix} \geq 0$ 이 성립한다.

그리고 우리가 보이고 싶은 것은 $S$ 가 PSD 라는 것이다. $g(y)$ 는 $f(x,y)$에서 $x$ 가 $x^*$ 로 고정된 것이기 때문에 $S \succeq 0$ 이다.

$\left( \Leftarrow \right)$

PSD의 definition을 사용하자. 즉, 모든 $y$ 에 대해 다음이 성립한다.

또한 앞선 $g(y)$의 정의를 생각해보면, $g(y) \leq f(x,y)$ 이다. 따라서 $\forall (x,y)$에 대해 $0 \leq f(x,y)$ 의 관계가 성립한다.

즉, $X$는 PSD 이다.

Reference

카이스트 서창호 교수님 강의 - EE424: 최적화개론 lecture 12.