3장 데이터 마트

1절 데이터 변경 및 요약

(1) 데이터 웨어하우스와 데이터 마트

데이터 웨어하우스

• 사용자의 의사결정 지원을 위해 데이터를 분석 가능한 형태로 저장한 중앙 저장소로서, 정보(data)와 창고(warehouse)의 합성어이다.
• 기존 정보를 활용해 더 나은 정보를 제공하고, 데이터의 품질을 향상시키며, 조직의 변화를 지원하고 비용과 자원관리의 효율성을 향상시키는 것이 목적이다.

[특징]

• 통합성 : 다양한 데이터 원천으로부터 데이터를 모두 통합하여 관리한다.
• 주제 지향성 : 주제를 중심으로 구성되며, 따라서 최종 사용자가 이해하기 쉬운 형태를 가진다.
• 시계열성 : 기존 운영 시스템은 최신 데이터를 유지하는데 반해, 데이터웨어하우스는 시간에 따른 변경 이력 데이터를 보유한다.
• 비휘발성 : 데이터 웨어하우스에 저장되는 데이터는 삭제 및 변경되지 않고, 일단 적재가 완료되면 읽기 전용 형태의 스냅 샷 데이터로 존재한다.

데이터 마트

• 데이터 웨어하우스와 사용자 사이의 중간층에 위치한 것으로, 하나의 주제 또는 하나의 부서 중심의 데이터 웨어하우스라고 할 수 있다.
• 데이터 마트 내 대부분의 데이터는 데이터 웨어하우스로부터 복제되지만, 자체적으로 수집될 수도 있으며, 관계형 데이터 베이스나 다차원 데이터베이스를 이용하여 구축한다.

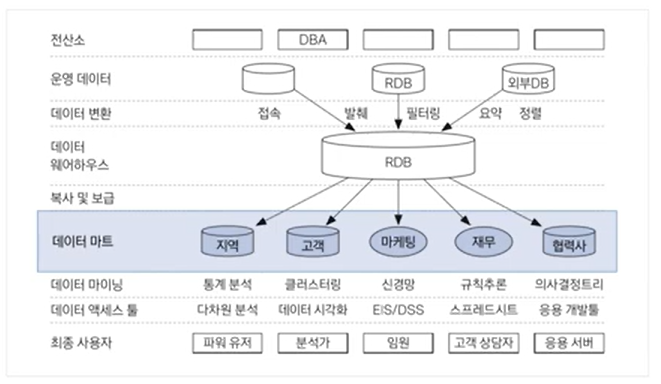
• 전산소, 운영데이터, 데이터 변환을 통해서 데이터 웨어하우스가 형성이 되고, 데이터 웨어를 통해서 복사와 보급하여 데이터 마트를 만들 수 있게 된다.

(2) 파생변수와 요약변수(중요)

파생변수

• 사용자(분석자)가 특정 조건을 만족하거나 특정 함수에 의해 값을 만들어 의미를 부여한 변수이다.
• 매우 주관적일 수 있으므로 논리적 타당성을 갖추어 개발해야 한다.
• 세분화, 고객행동 예측, 캠페인 반응 예측에 매우 잘 활용된다.
• 상황에 따라 특정 상황에서만 유의미하지 않게 대표성을 나타나게 할 필요가 있다.
• 근무시간 구매지수, 주 구매 매장 변수, 주 활동 지역 변수, 주 구매 상품 변수 등

요약변수

• 수집된 정보를 분석에 맞게 종합한 변수이다.
• 데이터마트에서 가장 기본적인 변수로 총 구매금액, 금액, 횟수, 구매여부 등 데이터 분석을 위해 만들어지는 변수이다.
• 많은 모델을 공통으로 사용될 수 있어 재활용성이 높다.
• 합계, 횟수와 같이 간단한 구조이므로 자동화하며 상황에 맞게 또 일반적으로 자동화 프로그램으로 구축 가능하다.
• 요약변수의 단점은 얼마 이상이면 구매하더라도 기준값의 의미 해석이 애매할 수 있다. 이러한 경우, 연속형 변수를 그룹핑해 사용하는 것이 좋다.
• 기간별 구매 금액, 기간별 구매 횟수, 상품별 구매 금액, 상품별 구매 순서 등

(3) R 패키지를 활용한 데이터 마트 개발

reshape 패키지 : 분해 및 재조합 (중요)

• 핵심 함수 : melt(), cast()
• melt() : 철을 녹이고 다시 틀에 넣어 모양을 만드는 과정에 비유하여, 녹이는 함수
• cast() : 모양을 만드는 함수
• 변수를 조합해 변수명을 만들고 변수들을 시간, 상품 등의 차원에 결합해 다양한 요약변수와 파생변수를 쉽게 생성하여 데이터마트를 구성할 수 있게 한다.

sqldf 패키지

• R에서 sql의 명령어를 사용하게 해주는 패키지
• SAS에서의 proc sql과 같이 R에서 활용 가능

plyr 패키지

• apply함수에 기반해 데이터와 출력변수를 동시에 배열로 치환하여 처리하는 패키지
• Split(데이터 분할)-apply(특정 함수 적용)-combine(결과 재조합) : 데이터를 분리하고 처리한 다음, 다시 결합하는 등 필수적인 데이터 처리 기능 제공

데이터 테이블 패키지 : data.table()

• 큰 데이터를 탐색, 연산, 병합하는데 아주 유용하다.
• 기존 data.frame방식보다 월등히 빠른 속도
  • 특정 컬럼을 키 값으로 색인을 지정한 후 데이터를 처리한다.
  • 빠른 그루핑과 ordering, 짧은 문장 지원 측면에서 데이터프레임보다 유용하다.

2절 데이터 탐색

(1) 탐색적 자료 분석(Exploratory Data Analysis, EDA)

• 다양한 차원과 값을 조합해가며 특이한 점이나 의미 있는 사실을 도출하고 분석의 최종목적을 달성해가는 과정으로, 데이터의 특징과 내재하는 구조적 관계를 알아내기 위한 기법들의 통칭이다.
• 데이터의 값을 눈으로 보면서 전체적인 추세와 어떤 특이사항이 있는지 관찰할 수 있고, 여기서 사용되는 기본 도구는 도표(plot), 그래프(graph), 그리고 통계요약(summary statistic)이다.

(2) 결측값(Missing value) (중요)

• 결측값은 입력이 누락되어 값이 존재하지 않고 비어있는 값을 의미한다. 보통 NA,999999, ' ' (공백), Unknown, Not Answer, NULL 등으로 출력된다.
• 일반적으로 결측값이 있는 데이터는 정보 손실에 의한 상당한 편의(bias)를 야기할 수 있고, 데이터를 두고 분석하는 것을 어렵게 만들며, 분석의 효율성을 감소시킨다.
• 또한 분석 결과가 왜곡될 수도 있다. 따라서 반드시 데이터에 결측값이 존재하는지를 확인하고 처리해야 한다.
• 결측값 자체가 의미 있는 경우도 있다.
• 결측값 처리가 전체 작업 속도에 많은 영향을 준다.
• 결측값을 처리하기 위해서 시간을 많이 사용하는 것은 비효율적이다.
• R에서 결측치를 확인하는 대표적인 함수
  • complete.case() : 레코드(행)별로 결측값이 있는지 확인하여 결측인 경우 false를 반환를 잃을 가능성이 높음
  • is.na() : 모든 원소에 대해 결측값이 있는지를 확인하여 결측인 경우 true를 반환
• 결측값을 처리하는 방법으로 크게 단순 대치법과 다중 대치법이 있다.
  • 단순 대치법
    • complete analysis
      • 가장 단순한 방법으로 결측값이 존재하는 모든 레코드(행)을 삭제하는 방법
    • 평균 대치법
      • 관측 또는 실험을 통해 얻어진 데이터의 평균으로 대치하는 방법
    • 단순확률대치법
      • 평균대치법에서 추정량의 표준 오차를 과소 추정하는 문제를 보완하고자 고안된 방법
  • 다중 대치법
    • 단순대치법을 한 번만 하지 않고 m번의 대치를 통해 m개의 가상적 완전 자료를 만드는 방법

(3) 이상값(Outlier) (중요)

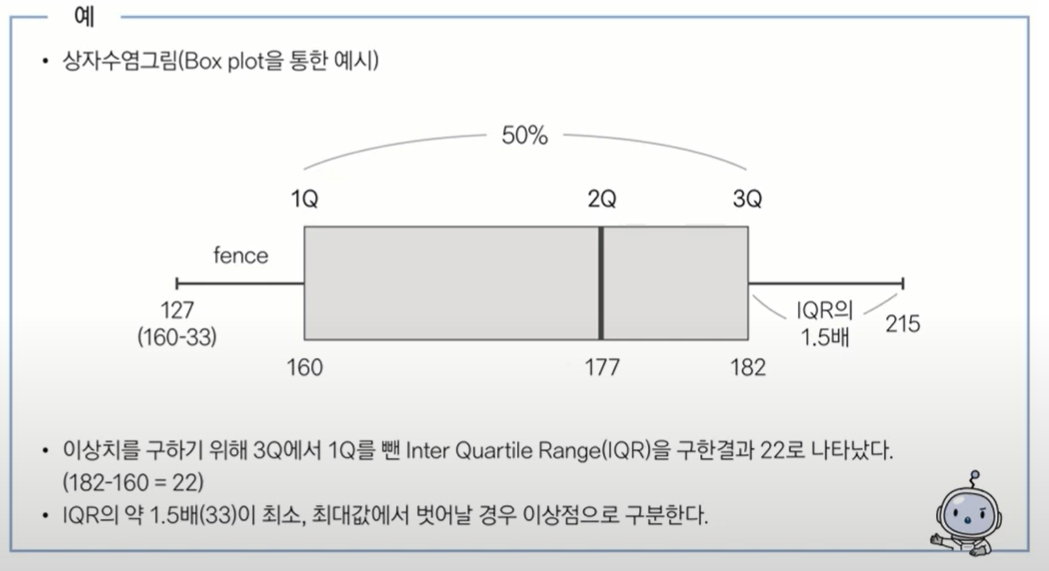
• 기하평균-2.5표준편차 < data < 기하평균+2.5표준편차
• 사분위수 이용하여 제거하기(상자 그림의 outer fence 밖에 있는 값 제거)
• 이상값 정의 : Q1-1.5(Q3-Q1) < data < Q3+1.5(Q3-Q1)
• 의도하지 않게 잘못 입력한 경우나 의도에 맞게 입력 되었으나 분석 목적에 부합하지 않아 제거해야 하는 경우 등 잘못된 데이터(Bad data)도 있지만, 의도하지 않은 현상이지만 분석에 포함해야 하는 경우와 의도된 이상값(Fraud, 불량)인 경우까지 다양하다.
• 일반적으로 이상값은 관측된 데이터의 범위에서 많이 벗어나 있는 아주 작거나 아주 큰 값으로, 정상 범위 밖에 있는 값을 뜻한다. 이러한 이상값은 잘못 입력된 값일 수도 있으나 실제로 존재하는 값일 수도 있으므로 분석의 목적이나 종류에 따라 적절한 판단이 필요하다.
• 이상치 판별은 상자그림으로 확인할 수 있으며, 이렇게 판단된 이상치는 상하위 5%에 해당하는 데이터를 삭제하거나 대치하는 등의 방법으로 처리할 수 있다.
• 상자그림 외에도 이상치를 평균으로부터 3표준편차 떨어진 값을 기준으로 판단하는 ESD(Extreme Studentized Deviation) 방법도 많이 사용된다.
• 극단값 절단(trimming)방법
  • 기하평균을 이용한 제거: geo_mean
  • 하단, 상단 % 이용한 제거 : 10% 절단 (상하위 5%에 해당되는 데이터 제거)
• 극단값 조정(winsorizing)방법
  • 상한값과 하한값을 벗어나는 값들을 하한, 상한값으로 바꾸어 활용하는 방법
  • 극단값 제거 방법에 비해 데이터 손실률이 적어 설명력이 높아지는 장점

(4) 구간화(Binning)

• 연속형 변수를 분석 목적에 맞게 활용하기 위해 구간화하여 모델링에 적용한다.
• 일반적으로 10진수 단위로 구간화 하지만, 구간을 5개로 나누는 것이 보통이며, 7개 이상의 구간은 잘 만들지 않는다.
• 신용평가 모형, 고객 세분화 등 시스템으로 모형을 적용하기 위해서는 각 변수들을 구간화해서 구간별로 점수를 적용하는 스코어링 방식으로 많이 활용되고 있다.
• binning : 연속형 변수를 범주형 변수로 변형하는 방식, 각각 동일한 개수의 레코드를 50개 이하의 구간에 데이터를 할당하여 구간들을 병합하면서 구간을 줄여나가는 방식의 구간화 방법
• 의사결정나무 : 세분화 또는 예측에 활용되는 의사결정나무 모형을 활용하여 활용되는 입력 변수들을 구간화

(5) 변수 중요도

• 변수 선택법과 유사한 개념으로 모형을 생성하여 사용된 변수의 중요도를 살피는 과정이다.
• klaR 패키지
  • greedy.wilks(): 세분화를 위한 stepwise forward 변수 선택을 위한 패키지, 종속변수에 가장 영향력을 미치는 변수를 wilks lambda를 활용하여 변수의 중요도를 정리
  • wilk's Lambda=집단내분산/총분산