4장 통계분석
6절 주성분분석
(1) 주성분분석
주성분분석(Principal Component Analysis)
- 여러 변수들의 변량을 '주성분(Principal Component)'이라는 서로 상관성이 높은 변수들의 선형결합으로 만들어 기존의 상관성이 높은 변수들을 요약, 축소하는 기법
- 첫 번째 주성분으로 전체 변동을 가장 많이 설명할 수 있도록 하고, 두 번째 주성분으로는 첫 번째 주성분과는 상관성이 없어서(낮아서) 첫 번째 주성분이 설명하지 못하는 나머지 변동을 정보의 손실 없이 가장 많이 설명할 수 있도록 변수들의 선형 조합을 만듦
(2) 주성분분석의 목적
- 여러 변수들 간에 내재하는 상관관계, 연관성을 이용해 소수의 주성분으로 차원을 축소함으로써 데이터를 이해하기 쉽고 관리하기 쉽게 해줌
- 다중공선성이 존재하는 경우, 상관성이 없는(적은)주성분으로 변수들을 축소하여 모형 개발에 활용(회귀분석이나 의사결정나무(decision tree)등의 모형 개발 시 입력변수들간의 상관관계가 높은 다중공선성(multicollinearity)이 존재할 경우 모형이 잘못 만들어져 문제가 생김)
- 연관성이 높은 변수를 주성분분석을 통해 차원을 축소한 후에 군집분석을 수행하면 군집화 결과, 연산 속도 개선
- 기계에서 나오는 다수의 센서 데이터를 주성분분석으로 차원을 축소한 후에 시계열에 분포나 추세의 변화를 분석하면 기계의 고장(fatal failure) 징후를 사전에 파악하는데 활용
(3) 주성분분석 VS 요인분석(인자분석)
요인분석(Factor Analysis)
- 등간척도(혹은 비율척도)로 측정한 두 개 이상의 변수들에 잠재되어 있는 공통인자를 찾아내는 기법
공통점
- 모두 데이터를 축소하는데 활용됨, 원래 데이터를 활용해서 몇 개의 새로운 변수들을 만듦
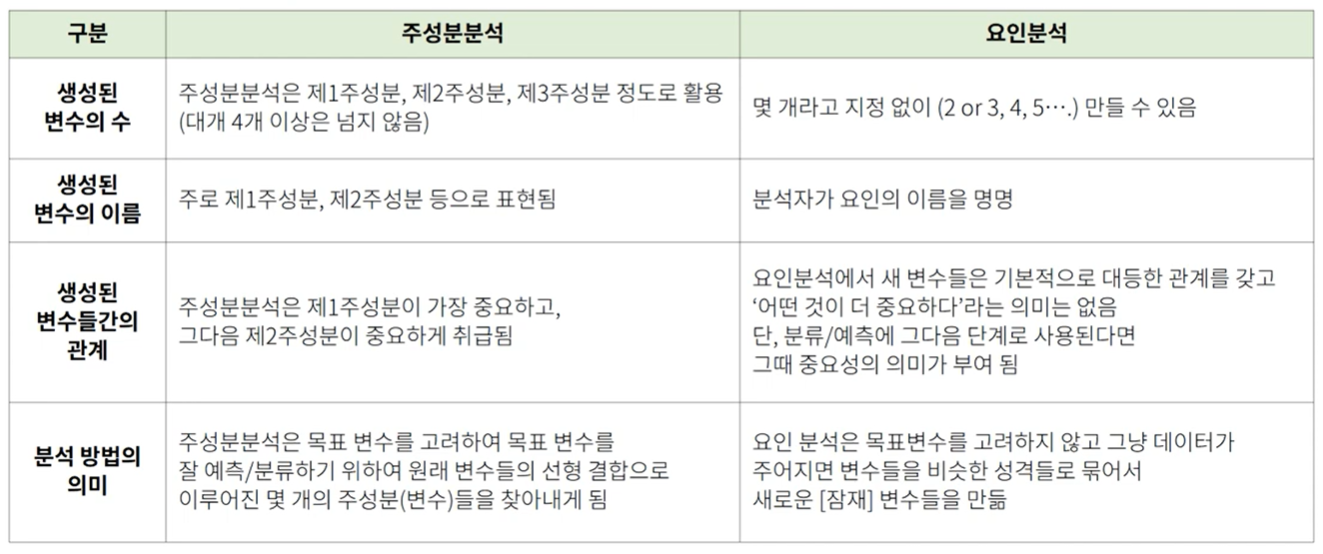
차이점
(4) 주성분의 선택법
- 주성분분석의 결과에서 누적기여율(cumulative proportion)이 85%이상이면 주성분의 수로 결정

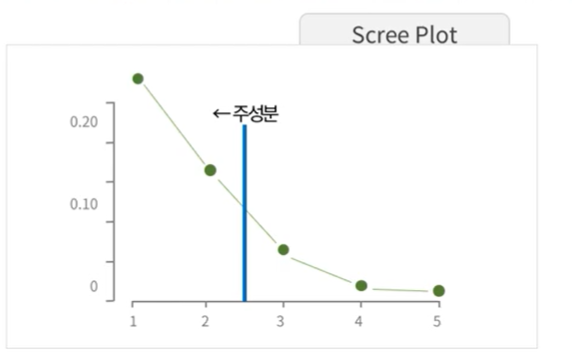
- scree plot을 활용하여 고윳값(eigenvalue)이 수평을 유지하기 전 단계로 주성분의 수를 선택
주성분분석 결과 해석
- 제1주성분, 제2주성분 누적 기여율 87.34%
- 제1주성분을 통한 기여율(해석률)은 55.23%이며, 제2주성분을 통한 기여율(해석률)은 32.11%
- 주성분의 개수를 정할 때는 누적 기여율을 가지고 정하거나 고윳값(eigenvalue)을 가지고 scree plot을 그려서 교윳값 곡선이 수평으로 눕는 주성분의 전 단계까지 활용함
