사람들이 인식하는 문서의 유사도는 주로 문서들 간에 동일한 단어 또는 비슷한 단어가 얼마나 공통적으로 많이 사용되었는지에 의존한다.
마찬가지로 기계가 계산하는 문서의 유사도의 성능은 각 문서의 단어들을 어떤 방법으로 수치화하여 표현했는지(DTM, Word2Vec등), 문서 간의 단어들의 차이를 어떤 방법(유클리드 거리, 코사인 유사도 등)으로 계산했는지에 달려있다.
1. 코사인 유사도(Cosine Similarity)
BoW에 기반한 단어 표현 방법인 DTM, TF-IDF, 또는 뒤에서 배우게 될 Word2Vec 등과 같이 단어를 수치화할 수 있는 방법을 이해했다면 이러한 표현 방법에 대해서 코사인 유사도를 이용하여 문서의 유사도를 구하는 게 가능하다.
1.1 코사인 유사도
코사인 유사도는 두 벡터 간의 코사인 각도를 이용하여 구할 수 있는 두 벡터의 유사도를 의미한다.
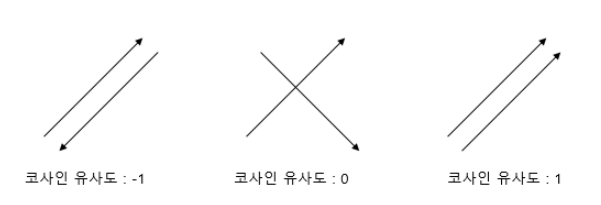
두 벡터의 방향이 완전히 동일한 경우에는 1의 값을 가지며, 90도의 각을 이루면 0, 180도로 반대의 방향을 가지면 -1의 값을 갖는다.
즉, 코사인 유사도는 -1 이상 1 이하의 값을 가지며 값이 1에 가까울 수록 유사도가 높다고 판단할 수 있다.
직관적으로 이해하면 두 벡터가 가리키는 방향이 얼마나 유사한가를 의미한다.
두 벡터 A, B에 대해서 코사인 유사도는 식으로 표현하면 다음과 같다.
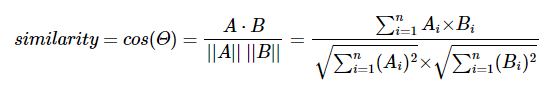
예제)
문서 단어 행렬(DTM)이나 TF-IDF 행렬을 통해서 문서의 유사도를 구하는 경우에는 문서 단어 행렬이나 TF-IDF 행렬이 각각의 특징 벡터 A, B가 된다.
문서1 : 저는 사과 좋아요
문서2 : 저는 바나나 좋아요
문서3 : 저는 바나나 좋아요 저는 바나나 좋아요
뛰어쓰기 기준 토큰화를 진행했다고 가정하고, 위의 세 문서에 대해서 문서 단어 행렬을 만들면 아래와 같다.
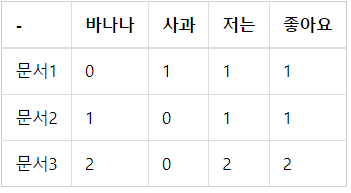
Numpy를 사용해서 코사인 유사도를 계산하는 함수를 구현하고 각 문서 벡터 간의 코사인 유사도를 계산해보자.
import numpy as np
from numpy import dot
from numpy.linalg import norm
def cos_sim(A, B):
return dot(A, B)/(norm(A)*norm(B))
doc1 = np.array([0,1,1,1])
doc2 = np.array([1,0,1,1])
doc3 = np.array([2,0,2,2])
print('문서 1과 문서2의 유사도 :',cos_sim(doc1, doc2))
print('문서 1과 문서3의 유사도 :',cos_sim(doc1, doc3))
print('문서 2와 문서3의 유사도 :',cos_sim(doc2, doc3))
# 문서 1과 문서2의 유사도 : 0.67
# 문서 1과 문서3의 유사도 : 0.67
# 문서 2과 문서3의 유사도 : 1.00- 문서3은 문서2에서 단지 모든 단어의 빈도수가 1씩 증가했을 뿐이고 유사도는 1로 동일하다.
- 이것이 시사하는 바는 다음과 같다.
- 만약 문서A, B는 동일 주제의 문서, 문서 C는 다른 주제의 문서라고 하고 문서 A와 문서 C의 문서의 길이는 거의 차이가 나지 않지만 문서 B의 경우 문서 A의 길이보다 두 배의 길이를 가진다고 가정하자.
- 이를 유클리드 거리로 유사도를 연산하면 문서 A가 문서 B보다 문서 C와 유사도가 더 높게 나오는 상황이 발생할 수 있다.
- 이는 유사도 연산에 문서의 길이가 영향을 받았기 때문이다.
- 코사인 유사도는 유사도를 구할 때 벡터의 방향(패턴)에 초점을 두므로 코사인 유사도는 문서의 길이가 다른 상황에서 비교적 공정한 비교를 할 수 있도록 도와준다.
2. 여러가지 유사도 기법
2.1 유클리드 거리(Euclidean distance)
유클리드 거리는 문서의 유사도를 구할 때 자카드 유사도나 코사인 유사도만큼 유용한 방법은 아니다.
다차원 공간에서 두개의 점 p와 q가 각각 p=(p1, p2, ..., pn)과 q = (q1, q2, ..., qn)의 좌표를 가질 때 두 점 사이의 거리를 계산하는 유클리드 거리 공식은 다음과 같다.
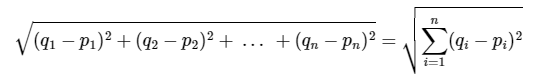
쉽게 2차원 공간에서 보자면 다음과 같다.
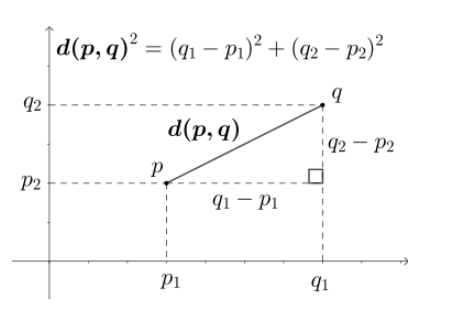
예시
아래와 같은 DTM에서 유클리드 거리를 통해 문서 Q와 가장 유사한 문서를 찾아내자
DTM
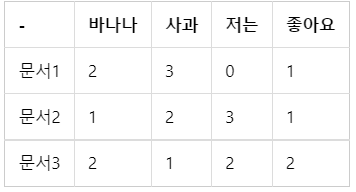
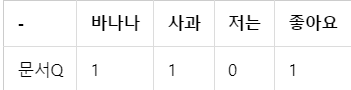
문서 Q
import numpy as np
def dist(x,y):
return np.sqrt(np.sum((x-y)**2))
doc1 = np.array((2,3,0,1))
doc2 = np.array((1,2,3,1))
doc3 = np.array((2,1,2,2))
docQ = np.array((1,1,0,1))
print('문서1과 문서Q의 거리 :',dist(doc1,docQ))
print('문서2과 문서Q의 거리 :',dist(doc2,docQ))
print('문서3과 문서Q의 거리 :',dist(doc3,docQ))
# 문서1과 문서Q의 거리 : 2.23606797749979
# 문서2과 문서Q의 거리 : 3.1622776601683795
# 문서3과 문서Q의 거리 : 2.449489742783178유클리드 거리의 값이 가장 작다는 것은 문서 간 거리가 가장 가깝다는 것을 의미한다.
2.2 자카드 유사도(Jaccard similarity)
A와 B 두개의 집합이 있다고 하자. 합집합에서 교집합의 비율을 구한다면 두 집합 A와 B의 유사도를 구할 수 있다는 것이 자카드 유사도(jaccard similarity)의 아이디어이다.
자카드 유사도는 0과 1사이의 값을 가지며 만약 두 집합이 동일하다면 1의 값을 가지고 두 집합의 공통 원소가 없다면 0의 값을 갖는다.
자카드 유사도 함수는 아래와 같다.
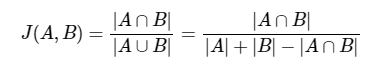
두 문서 doc1, doc2 사이의 자카드 유사도 J(doc1, doc2)는 두 집합의 교집합 크기를 두 집합의 합집합 크기로 나눈 값으로 정의 된다.
예시
doc1 = "apple banana everyone like likey watch card holder"
doc2 = "apple banana coupon passport love you"
# 토큰화
tokenized_doc1 = doc1.split()
tokenized_doc2 = doc2.split()
print('문서1 :',tokenized_doc1)
print('문서2 :',tokenized_doc2)
# 문서1 : ['apple', 'banana', 'everyone', 'like', 'likey', 'watch', 'card', 'holder']
# 문서2 : ['apple', 'banana', 'coupon', 'passport', 'love', 'you']문서1과 문서2의 합집합을 구하자.
union = set(tokenized_doc1).union(set(tokenized_doc2))
print('문서1과 문서2의 합집합 :',union)
# 문서1과 문서2의 합집합 : {'you', 'passport', 'watch', 'card', 'love', 'everyone', 'apple', 'likey', 'like', 'banana', 'holder', 'coupon'}문서1과 문서2의 교집합을 구하자.
intersection = set(tokenized_doc1).intersection(set(tokenized_doc2))
print('문서1과 문서2의 교집합 :',intersection)
# 문서1과 문서2의 교집합 : {'apple', 'banana'}교집합의 크기를 합집합의 크기로 나누자.
print('자카드 유사도 :',len(intersection)/len(union))
### 자카드 유사도 : 0.16666666666666666