자연어 처리에서 텍스트를 표현하는 방법으로는 여러가지 방법이 있다.
이번 챕터에서는 그 중 정보 검색과 텍스트 마이닝 분야에서 주로 사용되는 카운트 기반의 텍스트 표현 방법인 DTM(Document Term Matrix)과 TF-IDF(Term Frequency-Inverse Document Frequency)에 대해 다룬다.
1. 다양한 단어의 표현 방법
여기서는 카운트 기반의 단어 표현 방법 외에도 다양한 단어의 표현 방법에는 어떤 것이 있으며, 앞으로 어떤 순서로 단어 표현 방법을 학습하게 될 것인지에 대해 먼저 설명한다.
1.1 단어의 표현 방법
단어의 표현 방법은 크게 2가지 방법으로 나뉜다.
- 국소 표현(Local Representation)
- 해당 단어 그 자체만 보고, 특정값을 맵핑하여 단어를 표현하는 방법
- 분산 표현(Distributed Representation)
- 그 단어를 표현하고자 주변을 참고하여 단어를 표현하는 방법
예시
- 강아지, 귀여운, 사랑스러운이라는 단어가 있을 때
- 각 단어에 1번, 2번, 3번 등과 같은 숫자를 맵핑(mapping)하여 부여한다면 이는 국소 표현 방법에 해당한다.
- 강아지라는 단어 근처에는 주로 귀여운, 사랑스러운이라는 단어가 자주 등장하므로, 강아지라는 단어는 귀여운, 사랑스러운 느낌이다로 단어를 정의하는 것은 분산 표현 방법에 해당한다.
또한 비슷한 의미로 국소 표현 방법을 이산 표현(Discrete Representation), 분산 표현을 연속 표현(Continuous Representation)이라고도 한다.
1.2 단어 표현의 카테고리화
참고한 책은 아래와 같은 기준으로 단어 표현을 카테고리화하여 작성되었다.
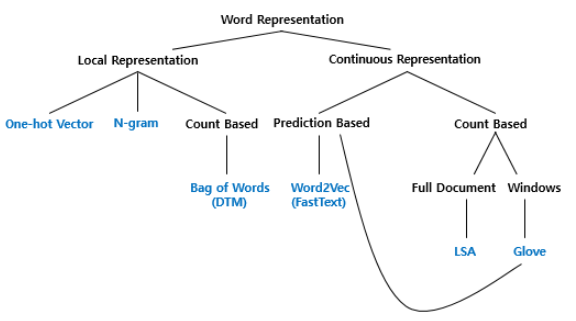
이번 글의 Bag of Words는 국소 표현(Local Representation)에 속하며, 단어의 빈도수를 카운트하여 단어를 수치화하는 단어 표현 방법이다. 이 글에서는 boW와 그의 확장인 DTM(또는 TDM)에 대해 학습하고, 이러한 빈도수 기반 단어 표현에 단어의 중요도에 따른 가중치를 줄 수 있는 TF-IDF에 대해서 학습한다.
워드 임베딩 글에서는 연속표현(Continuous Representation)에 속하면서, 예측(prediction)을 기반으로 단어의 뉘앙스를 표현하는 워드투벡터(Word2Vec)와 그의 확장인 패스트텍스트(FastText)를 학습하고, 예측과 카운트라는 두 가지 방법이 모두 사용된 글로브(GloVe)에 대해서 학습한다.
2. Bag of Words(boW)
단어의 등장 순서를 고려하지 않는 빈도수 기반의 단어 표현 방법
2.1 Bag of Words란?
- 단어들의 순서는 전혀 고려하지 않고, 단어들의 출현 빈도(frequency)에만 집중하는 텍스트 데이터의 수치화 표현 방법이다.
BoW를 만드는 과정을 두 가지 과정으로 생각해 보면
1. 단어 집합 생성 - 각 단어에 고유한 정수 인덱스를 부여한다.
2. 각 인덱스의 위치에 단어 토큰의 등장 횟수를 기록한 벡터를 만든다.
예제 - 문서1 : 정부가 발표하는 물가상승률과 소비자가 느끼는 물가상승률은 다르다.
문서1에 대해서 BoW를 만들어 보자. 아래의 함수는 입력된 문서에 대해서 단어 집합(vocaburary)을 만들어 각 단어에 정수 인덱스를 할당하고, BoW를 만든다.
from konlpy.tag import Okt
okt = Okt()
def build_bag_of_words(document):
# 온점 제거 및 형태소 분석
document = document.replace('.', '')
tokenized_document = okt.morphs(document)
word_to_index = {}
bow = []
for word in tokenized_document:
if word not in word_to_index.keys():
word_to_index[word] = len(word_to_index)
# BoW에 전부 기본값 1을 넣는다.
bow.insert(len(word_to_index) - 1, 1)
else:
# 재등장하는 단어의 인덱스
index = word_to_index.get(word)
# 재등장한 단어는 해당하는 인덱스의 위치에 1을 더한다.
bow[index] = bow[index] + 1
return word_to_index, bow해당 함수에 문서1을 입력으로 넣어보자
doc1 = "정부가 발표하는 물가상승률과 소비자가 느끼는 물가상승률은 다르다."
vocab, bow = build_bag_of_words(doc1)
print('vocabulary :', vocab)
print('bag of words vector :', bow)
# vocabulary : {'정부': 0, '가': 1, '발표': 2, '하는': 3, '물가상승률': 4, '과': 5, '소비자': 6, '느끼는': 7, '은': 8, '다르다': 9}
# bag of words vector : [1, 2, 1, 1, 2, 1, 1, 1, 1, 1]문서1에 각 단어에 대해서 인덱스를 부여한 결과는 첫번재 출력 결과이다.
문서1의 BoW는 두번째 출력 결과이다.
2.2 Bag of Words의 다른 예제들
문서2 : 소비자는 주로 소비하는 상품을 기준으로 물가상승률을 느낀다.
위의 함수에 임의의 문서2를 입력으로 하여 결과를 확인해 보자.
doc2 = '소비자는 주로 소비하는 상품을 기준으로 물가상승률을 느낀다.'
vocab, bow = build_bag_of_words(doc2)
print('vocabulary :', vocab)
print('bag of words vector :', bow)
# vocabulary : {'소비자': 0, '는': 1, '주로': 2, '소비': 3, '하는': 4, '상품': 5, '을': 6, '기준': 7, '으로': 8, '물가상승률': 9, '느낀다': 10}
# bag of words vector : [1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1]문서1과 문서2를 합쳐서 문서3이라고 명명하고 Bodw를 만들 수도 있다.
문서3 : 정부가 발표하는 물가상승률과 소비자가 느끼는 물가상승률은 다르다. 소비자는 주로 소비하는 상품을 기준으로 물가상승률을 느낀다.
doc3 = doc1 + ' ' + doc2
vocab, bow = build_bag_of_words(doc3)
print('vocabulary :', vocab)
print('bag of words vector :', bow)
# vocabulary : {'정부': 0, '가': 1, '발표': 2, '하는': 3, '물가상승률': 4, '과': 5, '소비자': 6, '느끼는': 7, '은': 8, '다르다': 9, '는': 10, '주로': 11, '소비': 12, '상품': 13, '을': 14, '기준': 15, '으로': 16, '느낀다': 17}
# bag of words vector : [1, 2, 1, 2, 3, 1, 2, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1]BoW는 종종 여러 문서의 단어 집합을 합친 뒤에, 해당 단어 집하에 대한 각 문서의 BoW를 구하기도 한다.
가령 문서3에 대한 단어 집합을 기준으로 문서1, 문서2의 BoW를 만든다고 한다면 아래와 같다.
문서3 단어 집합에 대한 문서1 BoW : [1, 2, 1, 1, 2, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0]
문서3 단어 집합에 대한 문서2 BoW : [0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 2, 1, 1, 1] BoW는 각 단어가 등장한 횟수를 수치화하는 텍스트 표현 방법이므로 주로 어떤 단어가 얼마나 등장했는지를 기준으로 문서가 어떤 성격의 문서인지를 판단하는 작업에 쓰인다.
즉, 분류 문제나 여러 문서 간의 유사도를 구하는 문제에 주로 쓰인다.
ex) '달리기', '체력', '근력' 같은 단어가 자주 등장하면 해당 문서를 체육 관련 문서로 분류
2.3 불용어를 제거한 boW 만들기
- 불용어 : 자연어 처리에서 별로 의미를 갖지 않는 단어들
- BoW를 사용한다는 것은 그 문서에서 각 단어가 얼마나 자주 등장했는지를 보겠다는 것이다.
- 각 단어에 대한 빈도수를 수치화 하겠다는 것은 결국 텍스트 내에서 어떤 단어들이 중요한지를 보고싶다는 의미를 함축하고 있다.
- BoW를 만들때 불용어를 제거하는 일은 자연어 처리의 정확도를 높이기 위해서 선택할 수 있는 전처리 기법이다,
사용자가 직접 정의한 불용어 or 라이브러리에서 제공하는 자체 불용어 등을 사용하여 불용어를 제거할 수 있다.
3. 문서 단어 행렬(Document-Term Matrix, DTM)
문서 단어 행렬은 서로 다른 문서들의 BoW를 결합한 표현 방법이다.(이하 DTM)
행과 열을 반대로 선택하면 TDM이라고 부르기도 한다.
3.1 문서 단어 행렬의 표기법
- 문서 단어 행렬이란 다수의 문서에서 등장하는 각 단어들의 빈도를 행렬로 표현한 것이다.
- 쉽게 생각하면 각 문서에 대한 BoW를 하나의 행렬로 만든 것으로 생각할 수 있으며, BoW와 다른 표현 방법이 아니라 BoW 표현을 다수의 문서에 대해서 행렬로 표현하고 부르는 용어이다.
예시
문서1 : 먹고 싶은 사과
문서2 : 먹고 싶은 바나나
문서3 : 길고 노란 바나나 바나나
문서4 : 저는 과일이 좋아요
띄어쓰기 단위 토큰화를 수행한다고 가정하고, 문서 단어 행렬로 표현하면 다음과 같다.
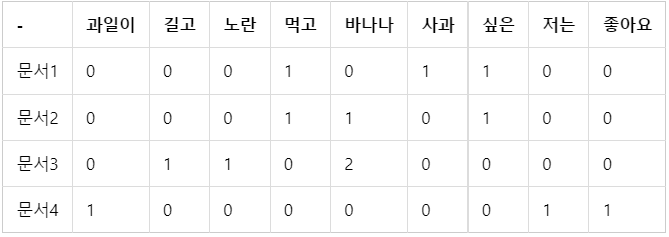
- 문서에서 등장한 단어의 빈도를 행렬의 값으로 표기
- 단어 행렬은 문서들을 서로 비교할 수 있도록 수치화할 수 있다는 점에서 의의를 갖는다.
- 만약 필요에 따라서는 형태소 분석기로 단어 토큰화를 수행하고, 불용어에 해당되는 조사들 또한 제거하여 더 정제된 DTM을 만들 수도 있을 것이다.
3.2 문서 단어 행렬의 한계
DTM은 매우 간단하고 구현하기도 쉽지만, 본질적으로 가지는 몇 가지 한계들이 있다.
3.2.1 희소 표현(Sparse representation)
- 원-핫 벡터는 단어 집합의 크기가 벡터의 차원이 되고 대부분의 값이 0이 되는 벡터이다.
- 이는 공간적 낭비와 계산 리소스를 증가시킬 수 있다는 점에서 단점을 가진다.
- DTM에서의 각 행을 문서 벡터라고 할 때 각 문서 벡터의 차원은 원-핫 벡터와 마찬가지로 전체 단어 집합의 크기를 가진다.
- 원-핫 벡터나 DTM과 같은 대부분의 값이 0인 표현을 희소 벡터(sparse vector) 또는 희소 행렬(sparse matrix)라고 부르는데, 희소 벡터는 많은 양의 저장 공간과 높은 계산 복잡도를 요구한다.
- 이러한 이유로 전처리를 통해 단어 집합의 크기를 줄이는 일은 BoW 표현을 사용하는 모델에서 중요할 수 있다.
3.2.2 단순 빈도 수 기반 접근
여러 문서에 등장하는 모든 단어에 대해서 빈도 표기를 하는 이런 방법은 때로는 한계를 가지기도 한다.
ex) 영어에 대해서 DTM을 만들었을 때
불용어인 the는 어떤 문서이든 자주 등장, 그런데 유사한 문서인지 비교하고 싶은 문서에서 동일하게 the가 빈도수가 높다고 해서 이 문서들이 유사한 문서라고 판단해선 안된다.
4. TF-IDF(Term Frequency-Inverse Document Frequency)
TF-IDF 가중치는 DTM 내에 있는 각 단어에 대한 중요도를 계산할 수 있다.
기존의 DTM을 사용하는 것보다 많은 정보를 고려하여 문서들을 비교할 수 있다.
TF-IDF가 DTM보다 항상 좋은 성능을 보장하는 것은 아니지만, 많은 경우에서 DTM보다 더 좋은 성능을 얻을 수 있다.
4.1 TF-IDF(단어 빈도-역 문서 빈도)
TF-IDF는 단어의 빈도와 역 문서 빈도(문서의 빈도에 특정 식을 취함)을 사용하여 DTM 내의 각 단어들마다 중요한 정도를 가중치로 주는 방법이다. 우선 DTM을 만든 후, TF-IDF 가중치를 부여한다.
TF-IDF는 TF와 IDF를 곱한 값을 의미하는데 이를 식으로 표현해 보자. 문서를 d, 단어를 t, 문서의 총 개수를 n이라고 표현할 때 TF, DF, IDF는 각각 다음과 같이 정의할 수 있다.
(1) tf(d, t) : 특정 문서 d에서의 특정 단어 t의 등장 횟수
TF는 앞에서 배운 DTM의 예제에서 각 단어들이 가진 값들이다. DTM이 각 문서에서의 각 단어의 등장 빈도를 나타내는 값이었기 때문이다.
(2) df(t) : 특정 단어 t가 등장한 문서의 수
특정 단어가 각 문서, 또는 문서들에서 몇 번 등장했는지는 관심가지지 않으며 오직 특정 단어 t가 등장한 문서의 수에만 관심을 가진다.
앞서 배운 DTM에서 바나나는 문서2와 문서3에서 등장했다. 이 경우 바나나의 df는 2이다.
(3) idf(d, t) : df(t)에 반비례하는 수
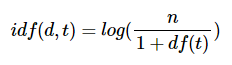
분모에 1을 더한 이유는 0이 되는 상황을 방지하기 위해서이다.
log를 사용하는 이유
- IDF를 DF의 역수(n/df(t))로 사용한다면 총 문서의 수n이 커질 수록, IDF의 값은 기하급수적으로 커지게 된다.
- 불용어 등과 같이 자주 쓰이는 단어들은 비교적 자주 쓰이지 않는 단어들보다 최소 수십 배 자주 등장한다. 그런데 비교적 자주 쓰이지 않는 단어들조차 희귀단어들과 비교하면 또 최소 수백 배는 더 자주 등장하는 편이다.
- 이에 log를 씌워주지 않으면 희귀단어들에 엄청난 가중치가 부여될 수 있다.
TF-IDF는 모든 문서에서 자주 등장하는 단어는 중요도가 낮다고 판단하며, 특정 문서에서만 자주 등장하는 단어는 중요도가 높다고 판단한다.
TF-IDF 값이 낮으면 중요도가 낮은 것이며, TF-IDF 값이 크면 중요도가 큰 것이다.
즉, The나 a와 같이 불용어의 경우에는 모든 문서에 자주 등장하기 마련이기 때문에 자연스럽게 불용어의 TF-IDF의 값은 다른 단어의 TF-IDF에 비해서 낮아지게 된다.
앞서 진행한 DTM을 통한 예제
1. 앞선 DTM을 가지고 진행 아래 DTM을 그대로 사용하면 각 문서에서의 각 단어의 TF가 된다.
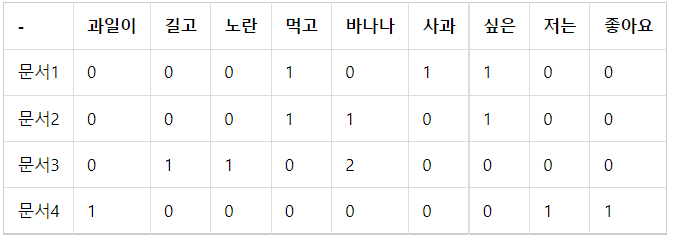
2. 이제 구해야 할 것은 TF와 곱해야할 값인 IDF이다. 로그의 밑은 임의로 정할 수 있는데 보통 자연로그(ln)가 사용된다.

문서의 총 수는 4이기 때문에 ln 안에서 분자는 4로 동일하다.
분모의 경우에는 각 단어가 등장한 문서의 수(DF)를 의미한다.
- TF-IDF를 계산해 보자.
앞서 사용한 DTM에서 단어 별로 위의 IDF값을 곱해주면 TF-IDF 값을 얻는다.

4.2 구현
- 위의 내용을 토대로 Python으로 직접 구현할 수 있습니다.
- 하지만 실제 TF-IDF 구현을 제공하고 있는 많은 머신 러닝 패키지들은 패키지마다 식이 조금씩 상이하지만, 위에서 배운 식과는 다른 조정된 식을 사용한다.
- 만약 전체 문서의 수 n이 4인데 df(t)의 값이 3인 경우에는 df(t)에 1이 더해지면서 log항의 분자와 분모의 값이 같아지게 되어 log를 씌우면 0이 되고 idf값이 0이 되면 가중치의 역할을 수행하지 못하는 문제가 있다.
- 따라서 기본적인 식의 몇가지 문제점으로 인해 조정된 식을 사용한다.
참고 문서
딥 러닝을 이용한 자연어 처리 - https://wikidocs.net/24557
