[백준 c++] 11048 이동하기

---

문제

https://www.acmicpc.net/problem/11048
N x M 크기의 미로는 1 x 1의 방으로 나누어져있다.
각 방에는 사탕이 놓여져있다.
(r, c)에 있으면, (r+1, c), (r, c+1), (r+1, c+1)로 이동할 수 있다.
(1, 1) 에서 시작해서 (N, M)까지 가려고 한다.
이 때, 얻을 수 있는 사탕의 최대 개수를 구하는 문제다.

---

풀이

Bottom Up dp를 이용해서 풀었다.
dp[r][c] = 사탕 개수

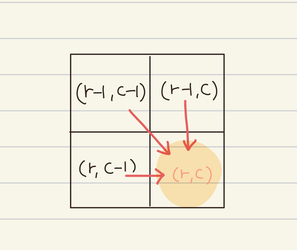
r,c 좌표는 3개 위치에서 올 수 있다.
즉 dp[r][c]가 최대가 되려면
이전 위치 中 , 사탕 개수의 최대값 + (r,c)의 사탕 개수

dp[r][c] = (r,c)의 사탕 개수+ max(dp[r - 1][c], dp[r][c - 1], dp[r - 1][c - 1])

Bottom up DP가 뭔지 감이 잡히는 듯🤨

---

코드

#include <iostream>
#include <algorithm>
using namespace std;
int n, m, k, dp[1001][1001];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            cin >> k;
            dp[i][j] = k + max(max(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]);
        }
    }
    cout << dp[n][m] << "\n";
}