[백준 c++] 1450 냅색문제

문제

https://www.acmicpc.net/problem/1450
N개의 물건을 C만큼의 무게를 넣을 수 있는 가방에 넣는 방법의 수를 구하는 문제다.

풀이

어려웠던 문제 🤕
처음 봤을 때 어라 이거 dp문제네 하고 금방 풀 수 있겠다고 생각했는데
무게 C는 1억보다 작거나 같은 음이 아닌 정수로 주어지기 때문에
기존 풀이처럼 배열 dp[100000000]로 저장할 수가 없다..

크기가 너무 커서 배열로 저장할 수 없는 경우엔 MITM(Meet In The Middle)로 풀면된다.

---

MITM

두 개의 벡터로 나눠서 DP값을 저장한다. 그리고 두 벡터 간의 조합(짝짓기)으로 풀 수 있다.

만약 물건 개수가 4, 가방 용량이 5일 때 입력이 1, 2, 3, 3 이라면 다음과 같이 dp 벡터를 구할 수 있다.이렇게 벡터 dp가 두 개 만들어졌으면 이제 가능한 조합의 개수를 구하면 된다.v1의 0의 입장에서 v2와 가능한(더해서 5를 넘지 않는) 경우의 수는 0,3,3이다. 이런식으로 다 더해주면 가능한 모든 경우의 수를 구할 수 있다.

이 짝짓기 작업은 upper_bound를 이용했다.

---

upper bound

upper bound는 정렬된 배열에서 어떤 값이 끝나는 위치를 반환한다.

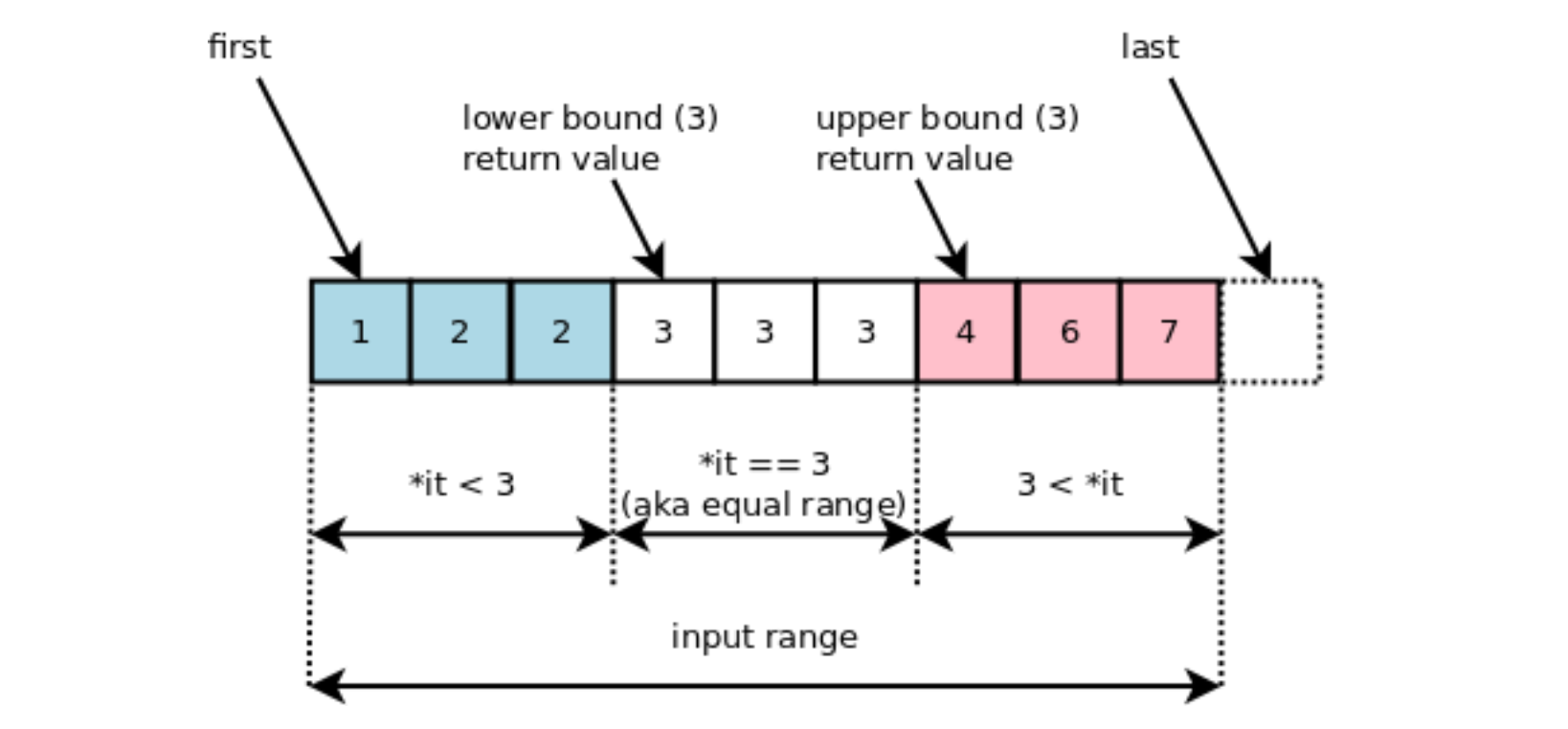
벡터 v에서 x값 다음 index를 찾고 싶다면?

int up = (int)(upper_bound(v.begin(),v.end(),x) - v.begin())

---

코드

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
ll n, c, ret, a[31];
vector<int> v, v2;
void go(int here, int _n, vector<int> &v, int sum)
{
    if (sum > c)
        return;
    if (here > _n)
    {
        v.push_back(sum);
        return;
    }
    go(here + 1, _n, v, sum + a[here]);
    go(here + 1, _n, v, sum);
    return;
}
int main()
{
    cin >> n >> c;
    for (int i = 0; i < n; i++)
        cin >> a[i];

    go(0, n / 2 - 1, v, 0); // 시작idx, 끝 idx, vector, sum
    go(n / 2, n - 1, v2, 0);

    sort(v.begin(), v.end());
    sort(v2.begin(), v2.end());
    
    for (int b : v)
        ret += (upper_bound(v2.begin(), v2.end(), c - b) - v2.begin());
        
    cout << ret << "\n";
}