[백준 c++] 17406 배열 돌리기 4

문제

크기 NxM의 배열 A가 있을 때, 배열 A의 값은 각 행에 있는 모든 수의 합 중 최소값을 의미한다.
배열은 K번의 회전 연산을 수행한다.
회전연산은 (r,c,s)로 나타내며 가장 왼쪽 윗 칸이 (r-s, c-s), 가장 오른쪽 아랫 칸이 (r+s, c+s)인 정사각형을 시계 방향으로 한 칸씩 돌린다는 의미이다. 배열의 칸 (r, c)는 r행 c열을 의미한다.

회전 연산= (3,4,2)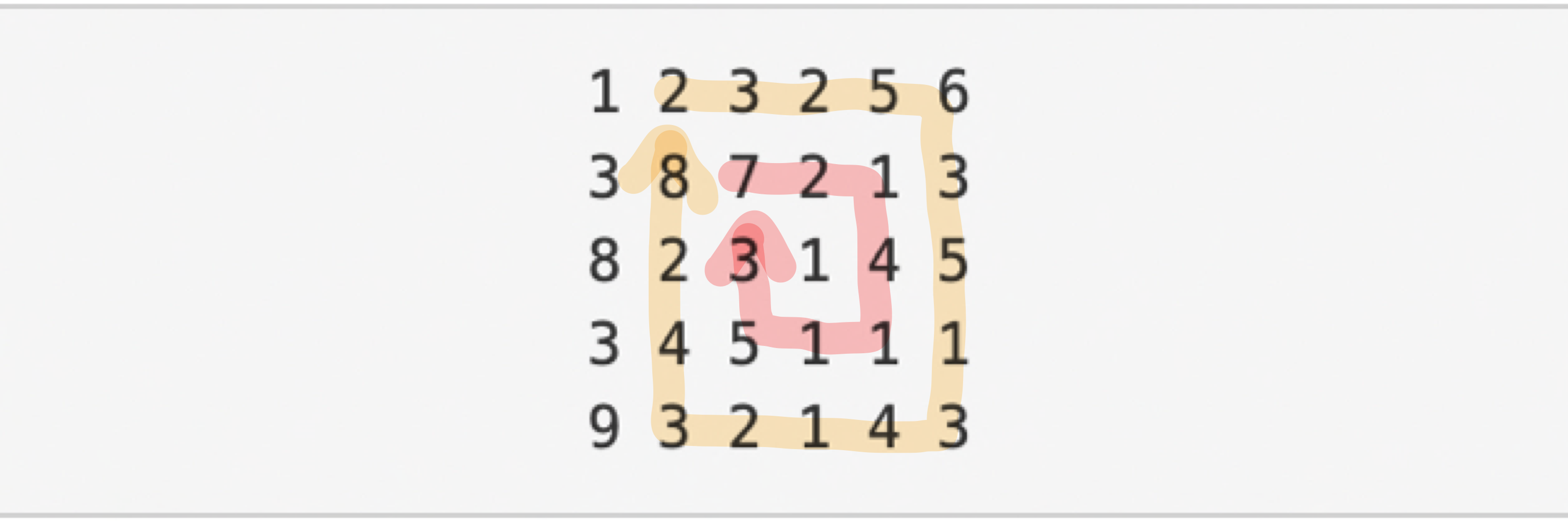결과

주어진 회전 연산은 모두 한 번씩 사용해야하며 회전 연산의 순서는 임의로 정할 수 있다.
배열 A의 값의 최소값을 출력하라

풀이

어떤 순서로 회전 연산을 진행해야 최소값을 가질 수 있을지 생각해야한다.
즉, 모든 경우의 수를 계산해야한다.

회전 연산 순서 정하기

next_permutation을 이용해서 순열을 구한다.

    for (int i = 1; i <= k; i++)
    {
        cin >> r >> c >> s;
        rot[i].push_back(r);
        rot[i].push_back(c);
        rot[i].push_back(s);
        v.push_back(i);
    }
    
    do
    {
        for (int i = 0; i < v.size(); i++)
            go(v[i]);
    } while (next_permutation(v.begin(), v.end()));

값 회전하기

진행 방향에 따른 (x,y)가중치 값을 pair로 저장한다.

pair<int,int> state[4] = [{0,1}, {1,0}, {0,-1}, {-1,0}]

for문을 이용해서 (r,c,s)의 범위만큼 값을 이동시켜준다.

코드

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int n, m, k, r, c, s, st, d, nxt, y, x, tmp, cnt, a[51][51], t[51][51], res = 987654321;
vector<int> v, rot[7];
pair<int, int> state[4];

void go(int idx)
{
    r = rot[idx][0];
    c = rot[idx][1];
    s = rot[idx][2];
    d = (r + s) - (r - s) + 1;
    y = r - s, x = c - s;
    while (d > 1)
    {
        int ny = y, nx = x;
        st = 0, nxt = -1, cnt = d;
        for (int i = 1; i <= 4 * (d - 1); i++)
        {
            tmp = t[ny][nx];
            t[ny][nx] = nxt;
            nxt = tmp;
            cnt--;
            if (cnt == 0)
            {
                cnt = d - 1;
                st++;
            }
            ny += state[st].first;
            nx += state[st].second;
        }
        t[y][x] = nxt;
        d -= 2;
        y++, x++;
    }
}
int main()
{
    cin >> n >> m >> k;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            cin >> a[i][j];
        }
    }
    for (int i = 1; i <= k; i++)
    {
        cin >> r >> c >> s;
        rot[i].push_back(r);
        rot[i].push_back(c);
        rot[i].push_back(s);
        v.push_back(i);
    }
    state[0] = {0, 1};
    state[1] = {1, 0};
    state[2] = {0, -1};
    state[3] = {-1, 0};
    do
    {
        copy(&a[0][0], &a[0][0] + 51 * 51, &t[0][0]);
        for (int i = 0; i < v.size(); i++)
            go(v[i]);
        for (int i = 1; i <= n; i++)
        {
            int hop = 0;
            for (int j = 1; j <= m; j++)
                hop += t[i][j];
            res = min(res, hop);
        }
    } while (next_permutation(v.begin(), v.end()));
    cout << res << "\n";
}