[백준 c++] 1915 가장 큰 정사각형

문제

https://www.acmicpc.net/problem/1915
N x M 크기의 0,1로 이루어진 배열이 있다.
이 배열에서 1로된 가장 큰 정사각형의 넓이를 구하는 문제다.

---

풀이

DP

dp를 쓰지 않으면 매 좌표에서 최대 정사각형 크기를 구해야하는데 매우 시간이 오래걸린다. 각 좌표에서 어떤 값을 저장해둬서 시간을 줄여야겠다고 생각했다.

❓그렇다면 어떤 값을 저장해야할까
어떤 좌표에서 가질 수 있는 정사각형의 최대 길이를 저장해두면
그 좌표가 지나온 길을 거치지 않고도 값을 구할 수 있겠다.

dp[y][x] = 이 좌표에서 가질 수 있는 정사각형의 최대 길이

❓ 이 좌표에서 가질 수 있는 정사각형의 최대 길이는 어떻게 구할까
세 방향에서 1이 이어지는 길이를 구한다.
이 세 개의 값 중에 min값+1 이 해당 좌표에서의 최대 정사각형 길이다.

재귀를 이용한 풀이

처음에 재귀로 푸는 방식을 택했다. 갈 수 있는 최대 길이니까 dfs가 생각났기 때문이다.

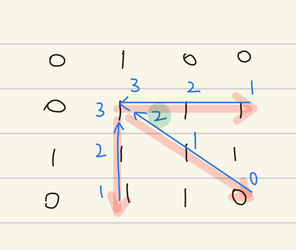
int go(int y, int x)
{
    if (y < 1 || x < 1 || y > n || x > m || !a[y][x])
        return 0;

    if (dp[y][x] != -1)
        return dp[y][x];

    dp[y][x] = min(min(go(y + 1, x), go(y, x + 1)), go(y + 1, x + 1)) + 1;

    return dp[y][x];
}

채점 결과 정답이긴 하지만 다른 사람들 시간보다 5배정도 차이가 나서 반복문으로 다시 풀어봤다.

반복문을 이용한 풀이

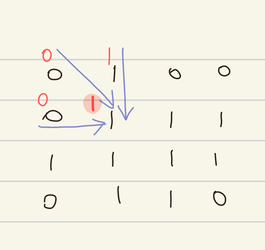
진행 방향을 반대로 생각하면 된다.

dp[y][x] = min(min(dp[y-1][x], dp[y][x-1]), dp[y-1][x-1]) +1

---

코드

#include <iostream>
#include <algorithm>
using namespace std;
int n, m, a[1001][1001], ret;

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            scanf("%1d", &a[i][j]);

    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            if (a[i][j] == 1)
                a[i][j] = min(min(a[i - 1][j], a[i][j - 1]), a[i - 1][j - 1]) + 1;
            ret = max(ret, a[i][j]);
        }
    }

    cout << ret * ret << "\n";
}