[백준 c++] 2234 성곽

문제 설명

https://www.acmicpc.net/problem/2234
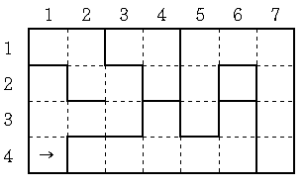대략 위의 그림과 같이 생긴 성곽이 있다. 굵은 선은 벽을 나타내고, 점선은 벽이 없어서 지나다닐 수 있는 통로를 나타낸다. 이러한 형태의 성의 지도를 입력받아서 다음을 계산하는 프로그램을 작성하시오.

1. 이 성에 있는 방의 개수
2. 가장 넓은 방의 넓이
3. 하나의 벽을 제거하여 얻을 수 있는 가장 넓은 방의 크기

위의 예에서는 방은 5개고, 가장 큰 방은 9개의 칸으로 이루어져 있으며, 위의 그림에서 화살표가 가리키는 벽을 제거하면 16인 크기의 방을 얻을 수 있다.

성은 M × N(1 ≤ M, N ≤ 50)개의 정사각형 칸으로 이루어진다. 성에는 최소 두 개의 방이 있어서, 항상 하나의 벽을 제거하여 두 방을 합치는 경우가 있다.

• 입력
  첫째 줄에 두 정수 N, M이 주어진다. 다음 M개의 줄에는 N개의 정수로 벽에 대한 정보가 주어진다. 벽에 대한 정보는 한 정수로 주어지는데, 서쪽에 벽이 있을 때는 1을, 북쪽에 벽이 있을 때는 2를, 동쪽에 벽이 있을 때는 4를, 남쪽에 벽이 있을 때는 8을 더한 값이 주어진다. 참고로 이진수의 각 비트를 생각하면 쉽다. 따라서 이 값은 0부터 15까지의 범위 안에 있다.

• 출력
  첫째 줄에 1의 답을, 둘째 줄에 2의 답을, 셋째 줄에 3의 답을 출력한다.

아이디어

비트마스킹 + DFS 를 이용해서 각 칸에 방 번호를 매긴다.
동쪽, 남쪽에 벽이 있다면 4+8= 12= 1100(2)

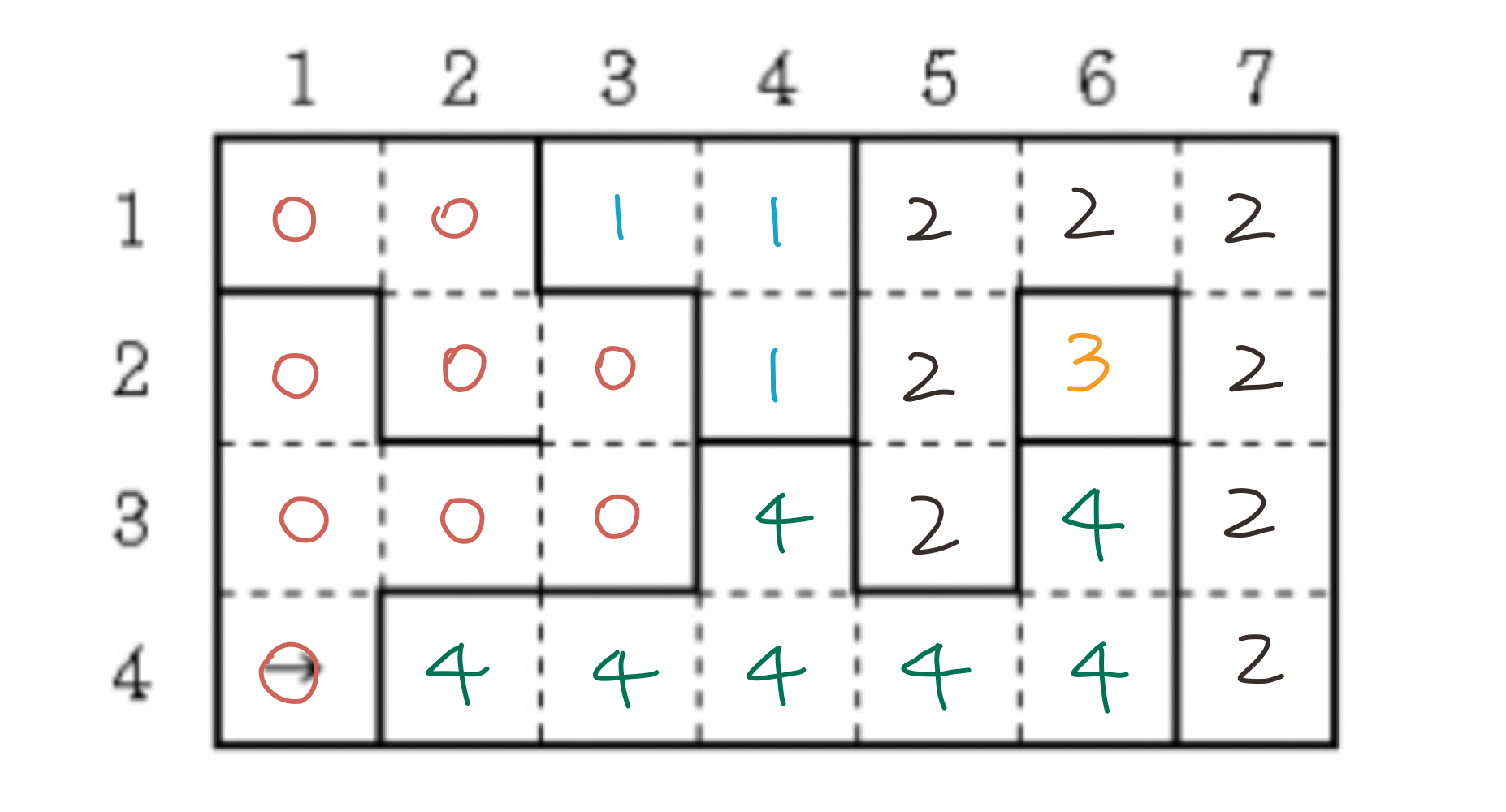
int a[y][x] = 8 //남쪽에 벽 0001

for (int i = 0; i < 4; i++)
{
  if (!(a[y][x] & (1 << i))) //=> 이 방향에 벽이 없다는 뜻
  {
  		dfs()
  }
}

함수 설명

• void dfs
  비트마스킹을 이용해서 벽이 없다면 dfs진행,
  2차원 배열 room에 방 번호rno 삽입,
  각 방의 넓이를 담는 배열 r_cnt[rno]++

• void dfs2
  각 방의 인접한 방 번호를 set v에 삽입

for문을 통해 각 방마다 이웃한 방과 넓이를 합쳤을 때 넓이를 구하고 이것의 max값을 구한다.

전체 코드

#include <iostream>
#include <set>
using namespace std;
int n, m, a[51][51], visited[51][51], visited2[51][51], room[51][51], rno, r_cnt[2504], res2, res3;
set<int> v[2504];
int dy[4] = {0, 1, 0, -1}, dx[4] = {1, 0, -1, 0};

void dfs(int y, int x)
{
    visited[y][x] = 1;
    room[y][x] = rno;
    r_cnt[rno]++;
    for (int i = 0; i < 4; i++)
    {
        if (!(a[y][x] & (1 << i)))
        {
            if (i == 0 && x - 1 >= 0 && !visited[y][x - 1])
                dfs(y, x - 1);
            if (i == 1 && y - 1 >= 0 && !visited[y - 1][x])
                dfs(y - 1, x);
            if (i == 2 && x + 1 < m && !visited[y][x + 1])
                dfs(y, x + 1);
            if (i == 3 && y + 1 < n && !visited[y + 1][x])
                dfs(y + 1, x);
        }
    }
}

void dfs2(int y, int x)
{
    visited2[y][x] = 1;
    int r = room[y][x];
    for (int i = 0; i < 4; i++)
    {
        int ny = dy[i] + y, nx = dx[i] + x;
        if (ny < 0 || nx < 0 || ny >= n || nx >= m)
            continue;
        if (room[y][x] != room[ny][nx])
            v[r].insert(room[ny][nx]);
        if (visited2[ny][nx])
            continue;
        dfs2(ny, nx);
    }
}

int main()
{
    cin >> m >> n;
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            cin >> a[i][j];
        }
    }

    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            if (!visited[i][j])
            {
                dfs(i, j);
                rno++;
            }
        }
    }

    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            if (!visited2[i][j])
            {
                dfs2(i, j);
            }
        }
    }

    for (int i = 0; i < rno; i++)
    {
        res2 = max(res2, r_cnt[i]);
        for (int x : v[i])
        {
            res3 = max(res3, r_cnt[i] + r_cnt[x]);
        }
    }
    cout << rno << "\n"
         << res2 << "\n"
         << res3 << "\n";
}