[백준 c++] 2583 영역 구하기

문제 설명

https://www.acmicpc.net/problem/2583
눈금의 간격이 1인 M×N(M,N≤100)크기의 모눈종이가 있다. 이 모눈종이 위에 눈금에 맞추어 K개의 직사각형을 그릴 때, 이들 K개의 직사각형의 내부를 제외한 나머지 부분이 몇 개의 분리된 영역으로 나누어진다.
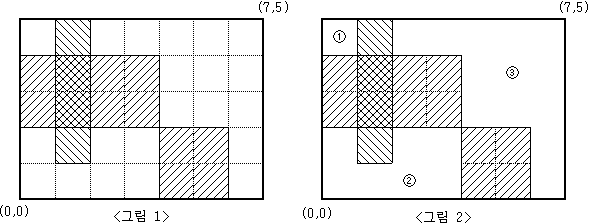위 그림의 경우 세 영역의 넓이는 각각 1, 7, 13이다.
M, N과 K 그리고 K개의 직사각형의 좌표가 주어질 때, K개의 직사각형 내부를 제외한 나머지 부분이 몇 개의 분리된 영역으로 나누어지는지, 그리고 분리된 각 영역의 넓이가 얼마인지를 구하여 이를 출력하는 문제다.

아이디어

연결된 컴포넌트의 개수를 구하는 문제로, DFS를 이용해서 풀었다.
다만, 기존에는 한 칸당 좌표가 주어졌다면 이 문제에선 꼭지점을 기준으로 좌표를 주기 때문에 꼭지점 좌표를 한 칸당 좌표로 바꾸는 과정이 필요했다.

직사각형의 왼쪽 아래 꼭지점의 좌표는 칸으로 바꿔도 좌표가 유지된다.
직사각형 오른쪽 아래 꼭지점의 좌표는 칸으로 바꾸면 x,y 각각 -1을 해준 좌표가 된다.

맨 왼쪽 아래 칸의 좌표와 맨 오른쪽 위 칸의 좌표를 구했다면 그 들 사이에 있는 나머지 칸을 채워주면 된다.

ex) (0,0)과 (1,1) 사이에 추가로 채워야할 칸의 좌표는 (0,1) (1,0)

전체 코드

#include <iostream>
#include <algorithm>
#include <stdio.h>
#include <queue>
#include <vector>
using namespace std;
int m, n, k, cnt = 0;
int a[101][101];       //배열
int visited[101][101]; //방문여부 2차원배열
int dy[4] = {-1, 0, 1, 0};
int dx[4] = {0, -1, 0, 1};
vector<int> w;
void dfs(int x, int y)
{
    cnt++;
    visited[x][y] = 1;
    for (int i = 0; i < 4; i++)
    {
        int nx = x + dx[i];
        int ny = y + dy[i];
        if (nx < 0 || ny < 0 || nx >= n || ny >= m)
            continue;
        if (visited[nx][ny] == 0 && a[nx][ny] == 0)
            dfs(nx, ny);
    }
}
int main()
{
    cin >> m >> n >> k; // y,x
    while (k--)
    {
        int x1, x2, y1, y2, cnt = 0;
        cin >> x1 >> y1 >> x2 >> y2;
        // cnt = (x2 - x1) * (y2 - y1); //작은 네모 개수

        //판에 색칠하자~~
        for (int i = y1; i < y2; i++)
        {
            for (int j = x1; j < x2; j++)
            {
                a[j][i] = 1;
            }
        }
        //(x,y)형태로
    }
    for (int i = 0; i < m; i++)
    {
        for (int j = 0; j < n; j++)
        {
            if (visited[j][i] == 0 && a[j][i] == 0)
            {
                cnt = 0;
                dfs(j, i);
                w.push_back(cnt);
            }
        }
    }
    sort(w.begin(), w.end());
    cout << w.size() << "\n";
    for (int i : w)
    {
        cout << i << " ";
    }
}