Hands-On Machine Learning Chapter 18 강화학습

강화학습(Reinforcement learning)의 대표적인 예시인 알파고에는 강화학습 분야 + 강력한 딥러닝을 적용하여 강력한 성능을 낸 것.

이번 장에서는 강화 학습이 무엇인지와 어떤 일을 가장 잘할 수 있는지, Deep reinforcement learning에서 가장 중요한 두 가지 정책인 Policy gardient와 심층 Q-네트워크(Deep Q-Network)을 마르코프 결정 과정(Markov decision process)를 소개 할 것이다. 또한 최신 알고리즘을 사용해 강력한 RL시스템을 구축할 수 있는 TF-Agents 라이브러리를 알아 보자.

18.1 보상을 최적화하기 위한 학습

강화 학습에서 소프트웨어 에이전트(Agent)는 관측(observation)을 하고 주어진 환경(environment)에서 행동(Action)을 하고, 그 결과로 보상(reward)를 받는다. 이때, 에이전트의 목적은 장기간 기대치를 최대로 만드는 것. 양의 보상은 최대로하거나 음의 보상은 최소로 만드는 것이다.

18.2 정책 탐색

소프트웨어 에이전트가 행동을 결정하기 위해 사용하는 알고리즘을 정책(Policy)라고 한다. 관측을 입력으로 받고 수행할 행동을 출력하는 신경망이 정책이 될 수 있다.

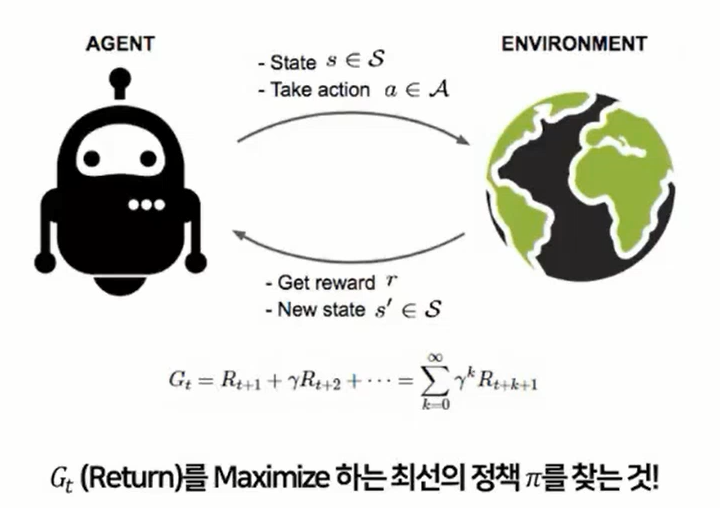
정책은 생각할 수 있는 어떤 알고리즘도 될 수 있으며 결정적일 필요가 없다. 어떠한 경우에는 환경을 관측할 필요도 없다. 예를들면 특정 시간 동안 수집한 먼지의 양을 보상으로 받는 로봇 진공청소기가 있다. 이때 정책은 매 초마다 어떤 확률 p만큼 전진하는 것일 수도 있고, (1-p)확률 만큼 r각도 정도로 왼쪽 또는 오른쪽으로 랜덤하게 회전하는 것일 수도 있다. 이때 로봇은 도달할 수 있는 어떤 장소라도 모두 찾아 먼지를 수집하려고 이상한 궤적을 만들 것이다. 이렇게 무작위성이 포함되어 있는 정책을 확률적 정책(Stochastic policy)가 있다. 이때 로봇 청소기에는 변경 가능한 두 개의 정책 파라미터(policy parameter) 확률p와 각도의 범위r이 있다. 이 파라미터에 많은 값을 시도해보고 가장 성능이 좋은 조합을 고르는 학습 알고리즘을 생각해 볼 수 있으나, 이는 좋지 못한 방법. 정책공간(plicy space)이 매우 크면 좋은 파라티터 조합을 찾기 어렵다.

정책공간을 탐색하는 다른 방법으로는 유전 알고리즘(genetic algorithm)이 있다. 이는 1세대 정책 100개를 랜덤하게 생성하여 실행한 후 80개는 버리고 20개는 살리고 각각 자신을 복사+약간의 무작위성을 더하는 자식 정책 4개를 생산하게 하는 것. 이를 여러 세대에 걸쳐서 진행한다.

또 다른 방법은 정책 파라미터에 대한 보상의 그라디언트를 평가해서 높은 보상의 방향을 따르는 그라디언트로 파라미터를 수정하는 최적화 기법 사용. 이를 정책 그라디언트(Policy gradient)라고 한다.

18.3 OpenAI 짐

최소한의 시뮬레이션 환경 구축. 이때, 환경을 만든 후 reset()메서드로 꼭 초기화해야 한다.

18.4 신경망 정책

이 신경망은 관측을 입력으로 받고 실행할 행동을 출력한다. 조금 더 정확히 말해 각 행동에 대한 확률을 추정하고, 추정된 확률에 따라 랜덤하게 행동한다. 예를들어 가능한 행동이 두 개만 있는 경우에는 하나의 출력 뉴련만 있으면 된다. 왼쪽이 p의 확률이라면, 오른쪽은 1-p의 확률. 예를 들어, 0.7을 출력했다면 왼쪽 행동은 70%의 확률로 선택할 것이고, 오른쪽은 30%의 확률로 선택될 것이다.

왜 가장 높은 점수의 행동을 그냥 선택하지 않고, 신경망이 만든 확률을 기반으로 랜덤하게 행동을 하는 것인가? 이는 에이전트가 새로운 행동을 탐험하는 것과 잘 할 수 있는 행동을 활용하는 것 사이에 균형을 맞추는 것.

이러한 특별한 환경에서는 과거의 행동과 관측은 무시해도 괜찮다. 각 관측이 환경에 대한 완전한 상태를 담고 있기 때문이다. 예를 들어 CartPole 모델에서 카트의 속도는 빼고 위치만 우리가 알고 있다면, 현재의 속도를 추정하기 위해 과거의 관측도 고려해야 한다. 또한 관측에 잡음이 있을 경우에는 가장 가능성 있는 현재의 상태를 추정하기 위해 지난 관측을 사용해야 한다.

18.5 행동 평가: 신용 할당 문제

각 Step에서 가장 좋은 행동이 무엇인지 알고 있다면, 평소처럼 추정된 확률과, 타깃 확률 사이의 크로스 엔트로피를 최소화하도록 신경망을 훈련할 수 있다. 이는 일반적인 지도 학습과 같으나, 강화학습에서 에이전트가 얻을 수 있는 가이드는 보상 뿐이다. 보상은 일반적으로 드물고 지연되어 나타난다. 예를 들어 에이전트가 100스텝 동안 막대의 균형을 유지했다면 이 100번의 행동 중 어떤 것이 좋고, 어떤 것이 나쁜지 알 수 있을까? 우리가 아는 것은 마지막 행동 뒤에 막대가 쓰러졌다는 것뿐. 그러나 모든 책임이 마지막 행동에 있는 것은 아니다. 이를 신용 할당 문제(credit assignmnet problem)라고 한다.

이를 해결하기 위해 흔히 사용하는 전략은 행동이 일어난 후 각 단계마다 할인 계수(discount factor) 감마를 적용한 보상을 모두 합하여 행동을 평가한다. 할인된 보상의 합을 행동의 Return이라 함. 이는 더 최신 값에 비중을 더 주지 않는다는 의미. 보통 0.9~0.99로 설정 우리는 이를 이용하여 평균적으로 다른 가능한 행동과 비교해서 각 행동이 얼마나 좋은지 혹은 나쁜지를 추정해야 한다. 이를 행동 이익(action advantage)라고 한다.

18.6 정책 그라디언트

PG 알고리즘은 높은 보상을 얻는 방향의 그라디언트를 따로도록 정책 파라미터를 최적화하는 알고리즘으로, 가장 인기 있는 것은 REINFORCE 알고리즘. 이는 다음과 같다.

1. 먼저 신경망 정책이 여러 번에 걸쳐 플레이하고, 매 스텝마다 선택된 행동이 더 높은 가능성을 가지도록 만드는 그라디언트 계산. 그러나 아직 이를 적용하지는 않는다.

2. 에피소드를 몇 번 실행한 다음, 각 행동의 이익을 계산한다.

3. 항 행동의 이익이 양수이면 이 행동이 좋은 것임을 의미하므로 미래에 선택될 가능성이 높도록 앞서 계산한 그라디언트를 적용. 그러나 행동 이익이 음수이면 이 행동이 나쁜 것이므로 미래에 이 행동이 덜 선택되도록 반대의 그라디언트 적용. 이는 각 그라디언트 벡터와 그 상응하는 행동의 이익 곱하면 된다.

4. 이후 모든 결과 그라디언트 벡터를 평균 내어 경사 하강법 스텝 수행.

하지만 이는 더 크고 복잡한 문제에는 잘 적용되지 못한다. 샘플 효율성(sample efficiency)가 좋지 못하기 때문이다. 즉 아주 긴 시간 동안 게임을 플레이해야 각 행동의 이익을 추정하여 정책을 개선할 수 있다.

18.7 마르코프 결정 과정

정책 그라디언트 알고리즘이 보상을 증가시키기 위해 정책을 직접적으로 최적화하는 반면, 마르코프 결정 과정은 덜 직접적이다. 즉, 에이전트가 각 상태에 할인된 미래의 대가를 추정하도록 한다. 또는 각 상태에 있는 각 행동에 대한 할인된 미래의 대가를 추정하도록 학습하고, 이 지식을 사용하여 어떻게 행동할지 결정한다. 이를 알기 위해서는 메모리가 없는 확률 과정 마르코프 연쇄에 대해 알아야 한다.

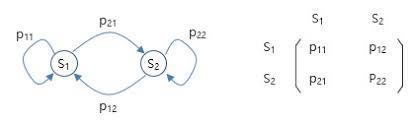
이 과정은 정해진 개수의 상태를 가지고 있으며, 각 스텝마다 한 상태에서 다른 상태로 랜덤하게 전이된다. 메모리가 없기에 한 곳에서 한 곳으로 가는 확률은 고정되어 있으며, 과거 상태에 영향을 받지 않고 오직 현재 상태에만 영향을 받는다. 여러번 확률을 진행하다 나갈 수 없는 공간에 갖춰지면 이를 종료 상태(Termunal state)라고 한다.

마르코프 결정 과정은 연쇄와 비슷하지만 다른 점이 있다. 각 스텝에서 에이전트는 여러 가능한 행동 중 하나를 선택할 수 있고, 전이 확률은 선택된 행동에 따라 달라진다. 또한 어떤 상태 전이는 보상을 반환한다. 이때 에이전트의 목적은 시간이 지남에 따라 보상을 최대화하기 위한 정책을 갖는 것.

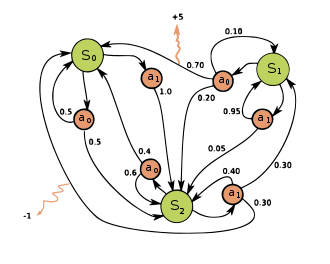
이떄, 최적의 상태 가치(State value)를 추정해야 한다. 이 값은 에이전트가 상태 s에 도달한 후 최적으로 행동한다고 가정하고 평균적으로 기대할 수 있는 할인된 미래 보상의 합. 이렇게 최적으로 행동하면 벨먼 최적 방정식(Bellman optimality equation)이 적용된다. 이 재귀적인 식이 의미하는 것은 에이전트가 최적으로 행동하면 현재 상태의 최적 가치는 하나의 최적 행동으로 인해 평균적으로 받게 될 보상과 이 행동이 유발할 수 있는 가능한 모든 다음 상태의 최적 가치의 기대치를 합한 것.

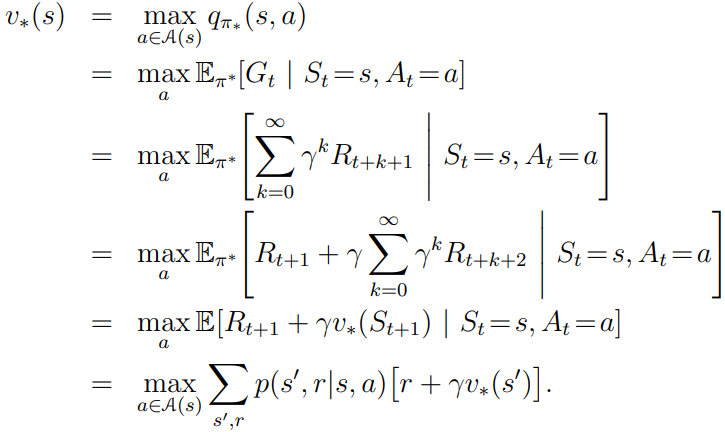
• p는 에이전트가 행동 a를 선택했을 때 상태 s에서 s'로 전이될 확률
• r은 에이전트가 행동 a를 선택해서 상태 s에서 s'로 전이되었을 때 에이전트가 받을 수 있는 보상.
• 감마는 할인 계수

이 식은 알고리즘이 가능한 모든 상태에 대한 최적의 상태 가치를 정확히 추정할 수 있도록 도와준다. 먼저 모든 상태 가치를 0으로 초기화 한후, 가치 반복(value iteration) 알고리즘을 사용하여 반복적으로 업데이트.

EX) V_(k)(S)는 k번째 반복에서 상태 s의 추정 가치

최적의 상태 가치를 아는 것은 정책을 평가할 때 유용하다. 하지만 에이전트를 위한 최적의 정책을 알려주지는 않는다. 이를 위해서 Q-value라고 부르는 최적의 상태-행동 가치를 추정할 수 있는 비슷한 알고리즘 존재. 상태-행동 (s,a) 쌍에 대한 최적의 Q-value인 Q*(s,a)는 에이전트가 상태 s에 도달하여 행동 a를 선택한 후 이 행동이 결과를 얻기 전에 평균적으로 기대할 수 있는 할인된 미래 보상의 합입니다. 여기서 에이전트는 이 행동 이후에 최적으로 행동할 것이라고 가정.

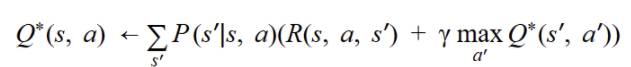
이 알고리즘은 다음과 같이 작동한다. 먼저 Q-value의 츄정을 모두 0으로 초기화한 후, Q-value 반복 알고리즘을 사용해 업데이트 한다. 최적의 Q-value를 구하면 최적의 정책을 정의하는 것은 쉽다. 에이전트가 상태s에 도달하였을 때, 가장 높은 Q-value가진 행동 선택.

18.8 시간차 학습

독립적인 행동으로 이루어진 강화 학습 문제는 보통 마르코프 결정 과정으로 모델링될 수 있지만, 초기에 에이전트는 전이 확률(T(s,a,s'))를 알지 못하며, 또한 보상이 얼마나 되는지도 모른다.((R(s,a,s')) 보상에 대해 알기 위해서는 적어도 한번은 각 상태와 전이를 경험해야 하며, 전이 확률에 대해 신뢰할 만한 추정을 얻으려면 여러 번 경험해야 한다.

시간차 학습(temporal difference learning)은 가치 반복 알고리즘과 비슷하지만, 에이전트가 MDP에 대해 일부 정보만 알고 있을 때를 다룰 수 있도록 변형한 것. 일반적으로 에이전트가 초기에 가능한 상태와 행동만 알고 다른 것은 모른다고 가정한다. 에이전트는 탐험 정책(exploration policy)을 사용해 MDP를 탐험한다. 탐험이 진행될수록 TD알고리즘이 실제로 고나측된 전이와 보상에 근거하여 상태 가치의 추정값을 업데이트 한다.

• 알파는 학습률
• r+감마*V_K(s')는 TD Taget
• 델타_k(s,r,s')는 TD error

18.9 Q-learning

Q-learning 알고리즘은 전이 확률과 보상을 초기에 알지 못하는 상황에서 Q-가치 반복 알고리즘을 적용한 것. Q-러닝은 에이전트가 플레이하게 하는 것을 보고 점진적으로 Q-가치 추정을 향상하는 방식으로 작동한다. 정확한 Q-가치 추정을 얻게되면 최적의 정책은 가장 높은 Q-가치를 가지는 행동을 선택하는 것.

각 상태-행동(s,a)쌍마다 이 알고리즘이 행동 a를 선택해 상태 s를 떠났을 때 에이전트가 받을 수 있는 보상 r과 기대할 수 있는 할인된 미래 보상의 합을 더한 이동 평균을 저장. 미래 보상의 합을 추정하기 위해서는 타깃 정책이 이후로 최적으로 행동한다고 가정하고 다음 상태 s'에 대한 Q-value 추정의 최댓값을 선택한다.

훈련된 정책을 반드시 실행에 사용하지 않기 때문에 Q-learning알고리즘을 off-policy 알고리즘이라고 한다. 훈련된 정책은 항상 높은 Q-VALUE를 가진 행동을 선택하는 것. 정책 그라디언트 알고리즘은 on-policy알고리즘. 훈련된 정책을 사용해 환경을 탐험한다.

18.9.1 탐험 정책

Q-learning은 탐험 정책이 MDP를 충분히 탐험해야 작동한다. 완전한 랜덤 정책이 결국에는 모든 상태와 전이를 여러 번 경험한다고 보장하지만, 이렇게 하려면 극단적으로 오랜 시간이 걸릴 수 있다. 그러므로, 엡실론-그리디 정책을 사용할 수 있다. 각 스텝에서 엡실론 확률로 랜덤하게 행동하거나, 1-엡실론 확률로 그 순간 가장 최선인 것(가장 높은 Q-value)를 선택하여 행동. 엡실론-그리디 정책의 장점은 Q-value 추정이 점점 향상되어, 환경에서 관심 있는 부분을 살피는 데 더 많은 시간을 사용한다는 점. 물론, MDP의 알려지지 않은 지역을 방문하는데에도 일정 시간을 사용하긴 할 것. 엡실론의 값은 높게(1.0)에서 시작하여 감소되는 것(0.05)가 일반적

또 다른 탐험 정책으로는 탐험의 가능성에 의존하는 대신 이전에 많이 시도하지 않았던 행동을 시도하도록 탐험 정책을 강조하는 방법이 있다.

18.9.2 근사 Q-러닝과 심층 Q-러닝

Q-러닝의 주요 문제는 많은 상태와 행동을 가진 대규모의 MDP에 적용하기 어렵다는 것. 이를 위해서 근사 Q-러닝 사용한다. 이는 어떤 (s,a)쌍의 Q-가치를 근사하는 함수를 적절한 개수의 파라미터를 사용하여 찾는 것. 오랫동안 상태에서 직접 뽑아낸 특성들을 선형 조합하는 방식이 권장되었지만, 심층 신경망을 사용해 복잡한 문제 더 나은 결과를 낼 수 있게 되었다. Q-추정하기 위해 사용하는 DNN을 심층 Q-네트워크(DQN)이라 하고, 근사 Q-러닝을 위해 DQN을 사용하는 것은 심층 Q-러닝이라고 한다.

DQN은 어떻게 훈련할 수 있을까? 주어진 (s,a)쌍에 대해 DQN이 계산한 Q-가치를 생각해보자. 벨먼 식으로 근사 Q-가치는 상태s에서 행동a를 실행했을 때 관측된 보상r과 그 이후에 최적으로 행동해서 얻은 할인된 가치를 더한 값에 가능한 한 가깝게 되어야 한다. 이 미래의 할인된 가치치를 추정하기 위해서는 간단하게 다음 상태 s'와 모든 가능한 행동a'에 대하여 DQN을 실행하면 된다. 그럼 모든 가능한 행동에 대한 미래의 근사 Q-가치를 얻을 수 있고, 그 다음으로 가장 높은 것을 고르고 할인을 적용하면 할인된 미래 보상의 추정을 얻을 수 있다.

이 타깃 Q-가치로 경사 하강법을 사용해 훈련 단계를 수행한다. 구체적으로 말하면 추정된 Q-가치와 타깃 Q-가치 사이의 제곱 오차를 후버손실을 이용해 최소화한다.

18.11 심층 Q-러닝의 변종

18.11.1 고정 Q-가치 타깃

기본 심층 Q-러닝 알고리즘에서 모델은 예측을 만들고 타깃을 설정하는 데 모두 사용된다. 이러한 피드백 순환 과정은 네트워크를 불안정하게 만들 수 있는데, 발산, 진동, 동결 등의 문제가 생긴다. 이를 해결하기 위하여 딥마인드에서는 두 개의 DQN모델을 사용했다. 첫 번째는 각 스텝에서 학습하고 에이전트를 움직이는 데 사용하는 온라인 모델이며, 두 번째는 타깃을 정의하기 위해서만 사용하는 타깃 모델이다.

이때, 타깃 모델은 온라인 모델보다 자주 업데이트되지 않으므로, Q-가치 타깃이 더 안정적이며 앞서 언급한 피드백 반복을 완화하고 이에 대한 영향이 감소한다.

18.11.2 더블 DQN

모든 행동이 동일하게 좋다고 가정하였을 때, 타깃 모델이 추정한 Q-가치가 동일해야 하지만 근사값이기 때문에 우연히 다른 것보다 조금 높은 값이 존재한다. 타깃 모델이 항상 가장 큰 Q-가치를 선택하므로, 평균 Q-가치보다 조금 더 커지며, 실제 Q-가치를 과대평가할 가능성이 높다. 이를 개선하기 위해 다음 상태에서 최선의 행동을 선택할 때 타깃 모델 대신 온라인 모델을 사용하도록 제안한다. 타깃 모델은 오직 최선의 행동에 대한 Q-가치를 추정할 때만 사용한다.

18.11.3 우선 순위 기반 경험 재성

재생 버퍼에서 경험을 균일하게 샘플링하는 것이 아니라, 중요한 경험을 더 자주 샘플링하면 어떨까? 하는 것에서 나온 아이디어가 중요도 샘플림(Importace sampling) 또는 우선 순위 기반 경험 재생(Prioritized Experience Replay,PER)이라고 한다. 구체적으로 말하면 어떤 경험이 학습 진행을 빠르게 만들면 '중요한' 것으로 간주한다.

18.11.4 듀얼링 DQN

Q-가치는 Q(s,a)=V(s)+A(s,a)처럼 표현될 수 있는데, 이때 V(s)는 상태s의 가치이고, A(s,a)는 상태 s에서 다른 모든 가능한 행동과 비교하여 행동a를 선택했을 때 이득이다. 또한 가치의 상태는 최선의 행동 a의 Q-가치와 같다(최적의 정책은 최선의 행동을 선택했다고 가정하였기 떄문). 이에 Q(s,a)=V(s) 이다. 즉, 듀얼링 DQN에서는 모델이 상태의 가치왁 ㅏ능한 각 행동의 이익을 모두 추정한다. 최선의 행동은 이익이 0이기 때문에 모델이 예측한 모든 이익에서 모든 최대 이익을 빼는 것.

18.13 그 외 유명한 강화 학습 알고리즘

- Actor critic 알고리즘

정책 그레디언트와 심층 Q-network를 결합한 형태. Actor critic 에이전트는 정책 네트워크와 DQN네트워크 두 개를 포함하는데, DQN은 에이전트의 경험을 통해 보통과 같이 훈련된다. 정책 네트워크는 일반적인 정책 그라이디언트와 다르게 훨씬 빠르게 훈련된다. 여러 에피소드를 진행하여 각 행동의 가치를 추정하고 각 행동의 할인된 미래 보상을 합하여 정규화하는 대신, 에이전트(Actor)는 DQN(critic)이 추정한 행동 가치에 의존. 결국 DQN의 도움을 받아 훈련하는 것.

- A3C

정책 그레디언트와 심층 Q-network를 결합한 형태. Actor critic 에이전트는 정책 네트워크와 DQN네트워크 두 개를 포함하는데, DQN은 에이전트의 경험을 통해 보통과 같이 훈련된다. 정책 네트워크는 일반적인 정책 그라이디언트와 다르게 훨씬 빠르게 훈련된다. 여러 에피소드를 진행하여 각 행동의 가치를 추정하고 각 행동의 할인된 미래 보상을 합하여 정규화하는 대신, 에이전트(Actor)는 DQN(critic)이 추정한 행동 가치에 의존. 결국 DQN의 도움을 받아 훈련하는 것.

- A2C

정책 그레디언트와 심층 Q-network를 결합한 형태. Actor critic 에이전트는 정책 네트워크와 DQN네트워크 두 개를 포함하는데, DQN은 에이전트의 경험을 통해 보통과 같이 훈련된다. 정책 네트워크는 일반적인 정책 그라이디언트와 다르게 훨씬 빠르게 훈련된다. 여러 에피소드를 진행하여 각 행동의 가치를 추정하고 각 행동의 할인된 미래 보상을 합하여 정규화하는 대신, 에이전트(Actor)는 DQN(critic)이 추정한 행동 가치에 의존. 결국 DQN의 도움을 받아 훈련하는 것.

- Soft Actor critic

Actor critic의 변종. 이는 모델의 보상뿐만 아니라, 행동의 엔트로피를 최대화하도록 학습하낟. 즉, 가능한 많은 보상을 얻으려고 하지만, 가능한 예측이 어렵도록 만든다는 것. 이는 환경을 탐색해서 훈련 속도를 높이고 DQN이 불완전한 추정을 만들 때 같은 행동을 반복해 실행하지 않도록 돕는다. 이 알고리즘은 놀라운 샘플링 효율성을 보여 학습속도가 매우 빨랐다.

- Actor critic 알고리즘

정책 그레디언트와 심층 Q-network를 결합한 형태. Actor critic 에이전트는 정책 네트워크와 DQN네트워크 두 개를 포함하는데, DQN은 에이전트의 경험을 통해 보통과 같이 훈련된다. 정책 네트워크는 일반적인 정책 그라이디언트와 다르게 훨씬 빠르게 훈련된다. 여러 에피소드를 진행하여 각 행동의 가치를 추정하고 각 행동의 할인된 미래 보상을 합하여 정규화하는 대신, 에이전트(Actor)는 DQN(critic)이 추정한 행동 가치에 의존. 결국 DQN의 도움을 받아 훈련하는 것.

- Actor critic 알고리즘

정책 그레디언트와 심층 Q-network를 결합한 형태. Actor critic 에이전트는 정책 네트워크와 DQN네트워크 두 개를 포함하는데, DQN은 에이전트의 경험을 통해 보통과 같이 훈련된다. 정책 네트워크는 일반적인 정책 그라이디언트와 다르게 훨씬 빠르게 훈련된다. 여러 에피소드를 진행하여 각 행동의 가치를 추정하고 각 행동의 할인된 미래 보상을 합하여 정규화하는 대신, 에이전트(Actor)는 DQN(critic)이 추정한 행동 가치에 의존. 결국 DQN의 도움을 받아 훈련하는 것.