합성곱 신경망(Convolutional neural network, CNN)은 대뇌의 시각 피질 연구에서 시작되었고, 이미지 인식 분야에서 사용되기 시작했다. 최근 몇 년 동안 컴퓨터 성능의 향상과 많은 양의 훈련 데이터, 11장에서 본 심층 신경망을 훈련시키기 위한 기술들을 바탕으로 CNN이 일부 복잡한 이미지 처리 문제에서 사람을 능가하는 성능을 달성하기 시작했고, 이 기술은 이미지 검색 서비스, 자율주행 자동차, 영상 자동 분류 시스템 등에 큰 기여를 했다.
14.1 시각 피질 구조
데이비드 허블과 토르스텐 비셀은 시각 피질 안의 많은 뉴런이 작은 국부 수용장을 가진다는 것을 보았다. 이때, 어떤 뉴런은 수평성의 이미지에만 반응하거나 반면 다른 뉴런은 다른 각도의 선분에 반응한다는 점을 보였다. 또한 어떤 뉴런은 큰 수용장을 가져서 저수준 패턴이 조합된 더 복잡한 패턴에 반응한다는 것을 알았고, 이러한 관찰은 고수준 뉴런이 이웃한 저수준 뉴런의 출력에 기반한다는 아이디어를 이끌어냈다.
이러한 발견은 이후 합성곱 신경망으로 점진적으로 진화되었고, 1998년 얀 르쿤의 논문에 의해 전환점을 맞게 되었다. 여기서 합성곱 층(Convolution layer)와 풀링 층(Pooling layer) 라는 새로운 구성 요소가 등장하게 된다.
14.2 합성곱 층
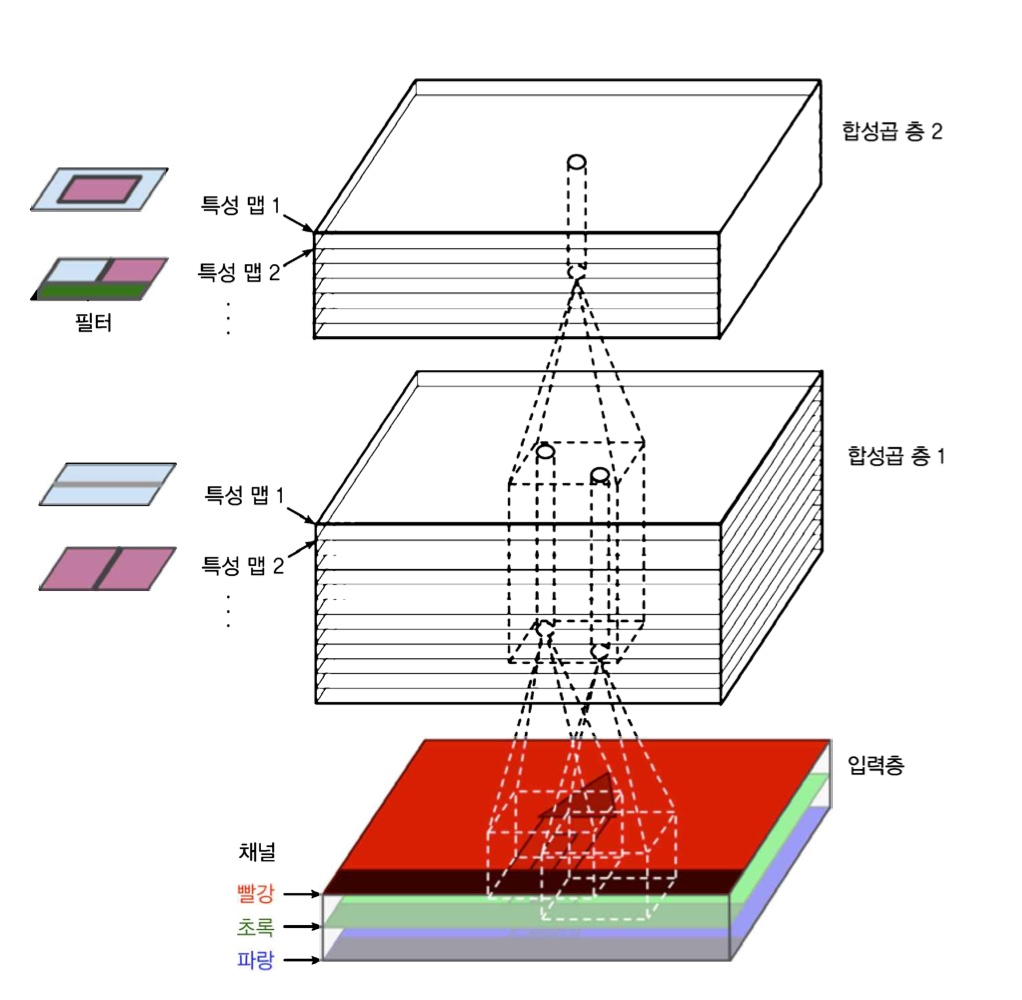
합성곱 층은 CNN의 가장 중요한 구성 요소이다. 첫 번째 합성곱 층의 뉴런은 입력 이미지의 모든 픽셀에 연결되는 것이 아니라 합성곱 층 뉴런의 수용장 안에 있는 픽셀에만 연결된다. 두 번째 합성곱 층에 있는 각 뉴런은 첫 번째 층의 작은 사각 영역 안에 위치한 뉴런에 연결된다. 이런 구조는 네트워크가 첫 번째 은닉층에서는 저수준 특성에 집중하고, 그 다음 은닉층에서는 더 큰 고수준 특성으로 조합해나가도록 도와준다.
이때, 아래 그림과 같이 높이와 너비를 이전 층과 같게 하기 위해 입력의 주위에 0을 추가하는데, 이를 제로 패딩(zero padding)이라고 한다.
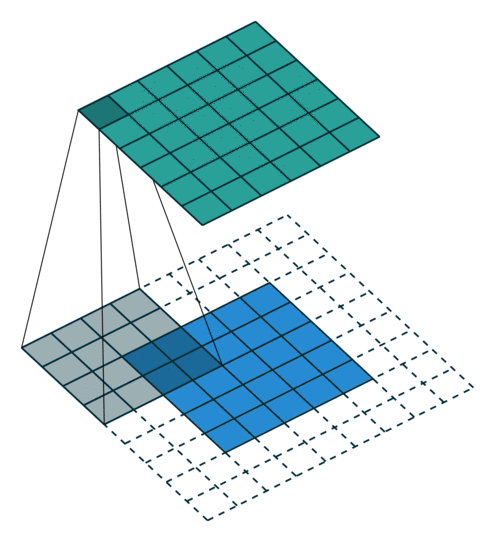
(공백 부분을 0으로 채워주는 것.)
수용장 사이에 간격을 두어 큰 입력층을 훨씬 작은 층에 연결하는 것도 가능하다. 이렇게 한다면 모델의 계산 복잡도를 크게 낮춰준다. 한 수용장과 다음 수용장 사이의 간격을 스트라이드(Stride)라고 한다.
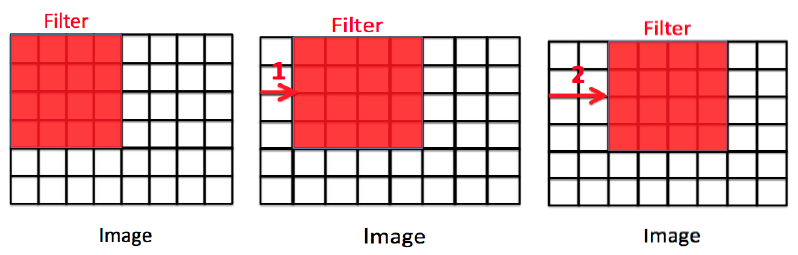
(가운데 처럼 CNN을 이용하면 Stride1, 오른쪽 처럼 CNN을 이용하면 Stride2)
14.2.1 필터
뉴런의 가중치는 수용장 크기의 작은 이미지로 표현될 수 있다. 예를 들어 필터(또는 합성곱 커널)이라 부르는 가중치 세트를 말한다. 층의 전체 뉴런에 적용된 하나의 필터는 하나의 특성 맵(Feature map)을 만든다. 이 맵은 필터를 가장 크게 활성화시키는 이미지의 영역을 강조한다. 수동으로 이러한 필터를 정의할 필요 없이, 훈련하는 동안 합성곱 층이 자동으로 해당 문제에 가장 유용한 필터를 찾고 상위층은 이들을 연결하여 더 복잡한 패턴을 학습한다.
14.2.2 여러 가지 특성 맵 쌓기
실제 합성곱 층은 여러 가지 필터를 가지고 필터마다 하나의 특성 맵을 출력하므로 3D로 표현하는 것이 더 정확하다. 각 특성 맵의 픽셀은 하나의 뉴런에 해당하고 하나의 특성 맵 안에서는 모든 뉴런이 같은 파라미터(즉, 동일한 가중치와 편향)를 공유하지만, 다른 특성 맵에 있는 뉴런은 다른 파라미터를 사용한다. 한 뉴런의 수용장은 앞서 설명한 것과 같지만, 이전 층에 있는 모든 특성 맵에 걸쳐 확장되는데, 간단히 말해 하나의 합성곱 층이 입력에 여러 필터를 적용하여 입력에 있는 여러 특성을 감지할 수 있다.
입력 이미지는 컬러 채널 마다 하나씩 여러 서브 층으로 구성되기도 한다. 컬러 채널은 보통 RGB를 말하는데, 흑백 이미지는 하나의 채널만 가질 수 있다. 하지만 가시광선 및 적외선 같은 이미지는 매우 많은 채널을 가질 수도 있다.

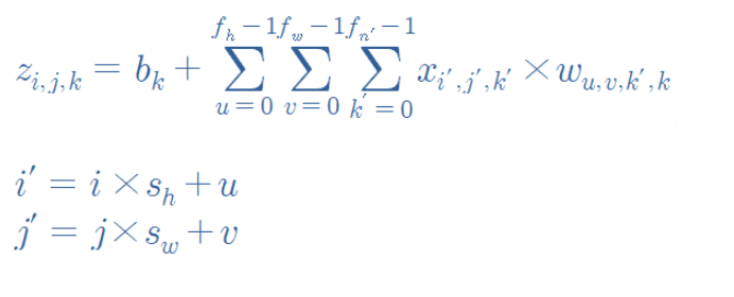
이는 합성곱 층에서 한 뉴런의 출력을 계산하는 법을 보여주는 식이다.
14.2.3 텐서플로 구현
텐서플로에서 각 입력 이미지는 보통[높이, 너비, 채널]형태의 3D 텐서로 표현된다. 하나의 미니배치는 [미니배치 크기, 높이, 너비, 채널]형태의 4D 텐서로 표현된다. 합성곱 층의 가중치는 [f_h,f_w,f_n',f_n]형태의 4D 텐서 표현된다. 합성곱 층의 편향은 간단하게 [f_n] 형태의 1D 텐서로 나타난다.
사이킷런의 load_sample_images()를 사용하여 두 개의 샘플 이미지를 로드한다.
cs
- 각 컬러 채널의 픽셀 강도는 0에서 255 사이의 값을 가진 바이트 하나로 표현. 이 특성을 255로 나누어 0에서 1사이의 값으로 바꾼다.
- 두 개의 7X7 필터를 만든다. (하나는 가운데 흰 수직선이 있고, 하나는 가운데 흰 수평선 존재)
- tf.nn.conv2d()함수를 이용해 제로패딩 및 스트라이드1 사용
- 만들어진 특성 맵 중 하나를 그래프로 그린다.
이때, tf.nn.con2vd()는 다음과 같은 함수이다.
- images는 입력의 미니배치(앞서 말한 것처럼 4D 텐서)
- Filters는 적용될 일련의 필터(앞서 말한 것처럼 4D 텐서)
- strides는 1이나 4개의 원소를 갖는 1D배열로 지정할 수 있다. 이때, 1D배열의 가운데 두 개의 원소는 수직, 수평 스트라이드이고, 현재는 첫 번째와 마지막 원소가 1이어야 한다.
- padding은 "VALID"(제로패딩 사용X)와 "SAME"(제로 패딩 사용O)중 하나 지정
위 예시에서는 필터를 직접 지정하였지만, 실제 CNN에서는 보통 훈련 가능한 변수로 필터를 정의하여 신경망이 가장 잘 맞는 필터를 학습한다. 이때 keras.layers.Con2D를 사용한다.
cs
이는 3X3 크기의 32개의 필터와 스트라이드1, 제로패딩을 사용하는 Conv2D층을 만들고 출력을 위해 ReLU활성화 함수를 적용한다.
14.2.4 메모리 요구 사항
CNN에 관련된 또 하나의 문제는 합성곱 층이 많은 양의 RAM을 필요로 한다는 점이다. 메모리 부족으로 훈련이 실패한다면 미니배치 크기를 줄여보거나, 스트라이드를 사용해 차원을 줄이는 등의 방법을 사용할 수 있다.
14.3 풀링 층
풀링 층의 목적은 계산량과 메모리 사용량, 과대적합의 위험을 줄여주는 파라미터 수를 줄이기 위해 입력 이미지의 서브샘플을 만드는 것이다.
풀링 층의 각 뉴런은 이전 층의 작은 사각 영역의 수용장 안에 있는 뉴런의 출력과 연결되어 있어, 이전과 동일하게 크기, 스트라이드, 패딩 유형을 지정해야 하지만 가중치는 없다. 즉, 최대나 평균 같은 합산 함수를 사용하여 입력값을 더하는 것이다.
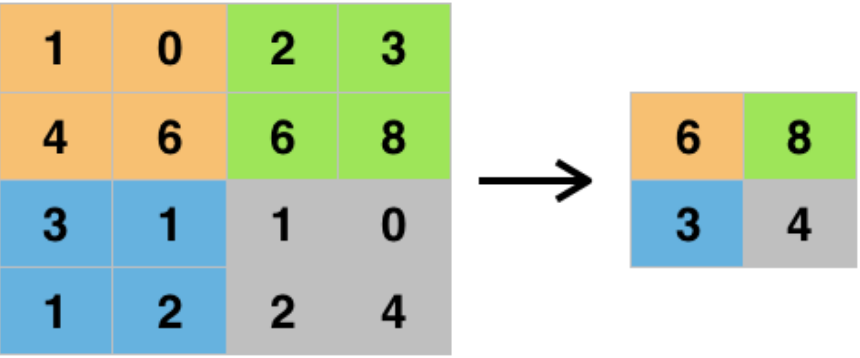
이는 가장 널리 이용되는 최대 풀링 층(max pooling layer)이다. 2X2 풀링 커널과 스트라이드2를 사용하는 것.
계산량, 메모리 사용량, 파라미터 수를 감소하는 것 외에도 최대 풀링은 작은 변화에도 일정 수준의 불변성(Invariance)을 만들어 준다. 이러한 불변성은 분류 작업처럼 예측이 이런 작은 부분에서 영향을 받지 않는 경우 유용할 수 있다.
물론 풀링은 단점도 가지고 있다. 2X2 풀링 커널과 스트라이드2만을 사용하여도 출력은 양방향으로 절반이 줄어들어 Input 값의 75%를 잃게 된다. 또한 시맨틱 분할과 같은 어떤 애플리케이션에서는 불변성을 필요로 하지 않을 수도 있다.
14.3.1 텐서플로 구현
다음 코드를 통해 2X2 커널을 사용하여 최대 풀링 층을 만든다. 스트라이드의 기본값은 커널 크기이므로, 이 층은 모두 스트라이드 2를 사용하고 기본적으로 "valid"패딩을 사용한다. 즉, 어떤 패딩도 하지 않는다.
cs
평균 풀링 층(Average pooling layer)을 만드려면 MaxPool2D 대신 AvgPool2D을 사용한다. 대부분 성능은 최대 풀링 층이 더 좋지만, 평균을 이용하게 되면 정보 손실이 더 적다. 그러나 최대 풀링은 의미 없는 것은 모두 제거하고 가장 큰 특징만 유지하므로 다음 층이 조금 더 명확한 신호로 작업할 수도 있으며, 최대 풀링은 평균 풀링보다 강력한 이동 불변성을 제공하고 연산 비용이 조금 덜 든다.
최대 풀링과 평균 풀링은 공간 차원이 아니라 깊이 차원으로 수행될 수 있다. 이를 통해 CNN은 다양한 특성에 대한 불변성을 학습할 수 있다. 이는 tf.nn.max_pool()함수를 사용하는데, 커널 크기와 스트라이드를 4개 원소를 가진 튜플로 지정한다. 이때, 첫 번째 세 값은 1이어야 하는데, 이는 배치, 높이, 너비 차원을 따라 커널 크기와 스트라이드가 1이라는 뜻이다.
cs
이를 케라스 모델의 층으로 만들고 싶으면 Lambda를 이용하면 된다.
cs
현대적인 신경망 구조에서 종종 보게될 마지막 풀링 층의 종류는 전역 평균 풀링 층이다. 이 층의 작동 방식은 각 특성 맵의 평균을 계산하는 것이다. 이는 입력과 공간 방향 차원이 같은 커널을 사용하는 풀링 층과 같다. 각 샘플의 특성 맵마다 하나의 숫자를 출력한다는 의미. 이는 keras.layers.GlobalAvgPool2D 클래스를 사용한다.
cs
cs
14.4 CNN 구조
전형적인 CNN 구조는 합성곱 층을 몇 개 쌓고(각 층마다 ReLU 층을 쌓는다), 그 다음 풀링층을 쌓고, 그 다음에 또 합성곱 층을 몇 개 더 쌓고, 그다음에 다시 풀링 층을 쌓는 식이다.
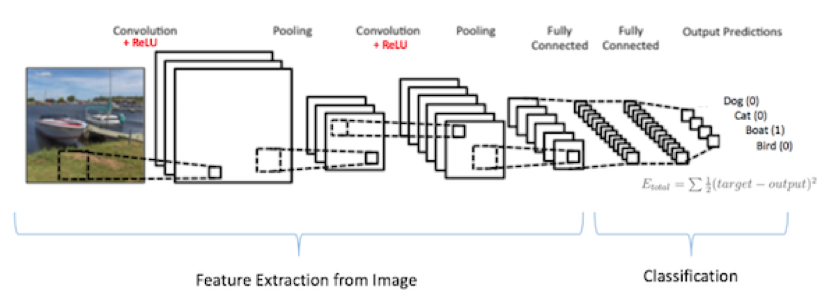
네트워크를 통과하여 진행할수록 이미지는 점점 작아지지만, 합성곱 층 때문에 일반적으로 점점 더 깊어지며 더 많은 특성 맵을 가진다. 맨 위층에서는 몇 개의 완전 연결 층과 ReLU로 구성된 일반적인 FNN이 추가되고, 마지막 층에서는 소프트 맥스 층 등을 통해 예측을 출력한다.
이때, 합성곱 층에 너무 큰 커널을 사용하는 것보다는 작은 커널을 여러 겹 쌓는 것이 더 좋은 성능을 낼 수 있다. 그러나 첫 번째 합성곱 층에서는 큰 크기의 커널을 사용한다.
다음 코드는 패션MNIST 테이터셋 문제를 해결하기 위한 간단한 CNN 코드이다.
cs
- 첫 번째 층은 64개의 큰 필터(7X7)와 스트라이드 1을 사용한다. 이미지가 28X28 픽셀 크기이고, 하나의 컬러 채널이므로 Input_shape=[28, 28, 1]로 지정
- 풀링 크기가 2인 최대 풀링 층 추가하여 차원을 절반으로 줄인다.
- 이와 동일한 구조를 두 번 반복.
- CNN이 출력층에 다다를수록 필터 개수가 늘어난다. 저수준 특성( EX) 작은 동심원, 수평성 )의 개수는 적지만 이를 연결하여 고수준 특성을 만들 수 있는 방법이 많기 때문에 이런 구조가 합리적이다. 풀링 층 다음에 필터 개수를 두 배로 늘리는 것이 일반적인 방법. 풀링 층이 차원을 절반으로 줄이므로 이어지는 층에서는 파라미터 개수, 메모리 사용량, 계산 비용을 크게 늘리지 않고 특성 맵 개수를 두 배로 늘릴 수 있다.
- 다음은 두 개의 은닉층과 하나의 출력층으로 구성된 완전 연결 네트워크. 이때 밀집 네트워크는 샘플의 특성으로 1D 배열을 필요로 하므로 일렬로 펼쳐야 한다. 또한 과대적합을 줄이기 위해 드롭아웃 층 추가.
14.4.1 LeNet-5
가장 널리 알려진 CNN구조로 1998년 얀 르쿤에 의해 탄생.
14.4.2 AlexNet
2012sus 탄생한 모델로, 구조는 더 크고 깊을 뿐 LeNet-5과 비슷하다. 처음으로 합성곱 층 위에 풀링 층을 쌓지 않고 바로 합성곱 층끼리 쌓았다. 또한 과대적합을 줄위기 위해 드롭아웃과 데이터 증식(Data augmentation)을 사용하였다.
또한 LRN(local response normalization)이라 부르는 정규화 단계를 사용했다. 이는 가장 강하게 활성화된 뉴런이 다른 특성 맵에 있는 같은 위치의 뉴런을 억제한다. 이는 특성 맵을 각기 특별하게 다른 것과 구분되게 하고, 더 넓은 시각에서 특징을 탐색하도록 만들어 결국 일반화 성능을 향상하게 한다.
14.4.3 GoogLeNet
이는 이전 CNN보다 훨씬 더 깊은 네트워크 구조를 가진다. 또한 인셉션 모듈(Inception module)이라는 서브 네트워크를 가지고 있어 이전의 구조보다 훨씬 효과적으로 파라미터를 사용한다.
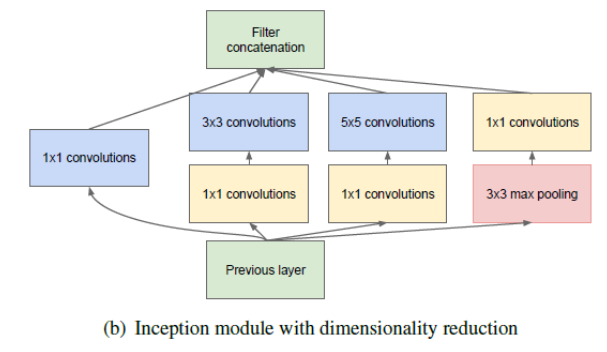
처음에 입력 신호가 복사되어 네 내의 다른 층에 주입된다. 모든 합성곱 층은 ReLU활성화 함수를 사용한다. 두 번째 합성곱 층은 각기 다른 커널 크기를 사용하여 다른 크기의 패턴을 잡는다. 이때, 모든 층은 스트라이드 1과 "same" 패딩을 사용하므로 출력의 높이와 너비가 모두 입력과 같다. 이렇게 연결 하면 모든 출력을 깊이 연결 층(depth concatenation layer)에서 깊이 방향으로 연결할 수 있다.
왜 처음에 1X1 커널의 합성곱 층을 가지는 것일까?
- 공간상의 패턴을 잡을 수는 없지만 깊이 차원을 따라 놓인 패턴을 잡을 수 있다.
- 입력보다 더 적은 특성 맵을 출력하므로 차원을 줄인다는 의미인 병목 층(Bottleneck layer)의 역할을 담당한다. 이는 연산 비용과 파라미터 개수를 줄여 훈련 속도를 높이고 일반화 성능을 향상한다.
- 합성곱 층의 쌍이 더 복잡한 패턴을 감지할 수 있는 한 개의 강력한 합성곱 층처럼 작동할 수 있다.
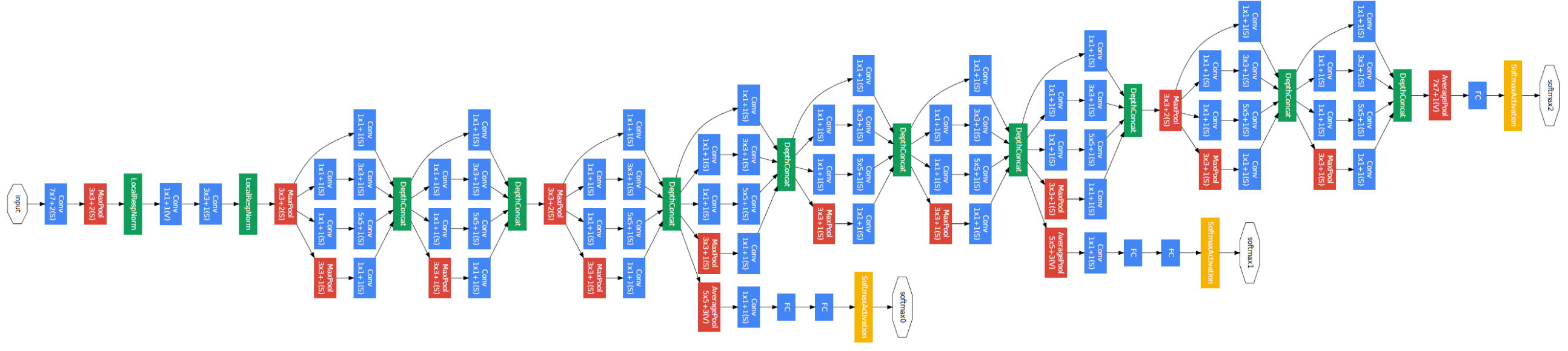
GoogLeNet은 다음과 같은 구조를 가진다.
14.4.4 VGGNet
이는 매우 단순하고 고전적인 구조를 가진다. 2개 또는 3개의 합성곡 층 뒤에 풀링이 나오고, 다시 2개 또는 3개의 합성곱 층과 풀링 층이 등장하는 식이다. 마지막 밀집 네트워크는 2개의 은닉층과 출력층으로 이루어지며, 오직 3X3의 필터만 사용한다.
14.4.5 ResNet
이 모델은 더 적은 파라미터를 사용해 점점 더 깊은 네트워크로 모델을 구성하는 일반적인 트렌드를 만들었다. 이런 깊은 네트워크를 훈련시킬 수 있는 핵심 요소는 스킵 연결(또는 숏컷 연결)이다. 즉, 어떤 층에 주입되는 신호가 상위 층의 출력에도 더해지게 되는 구조를 가진다.
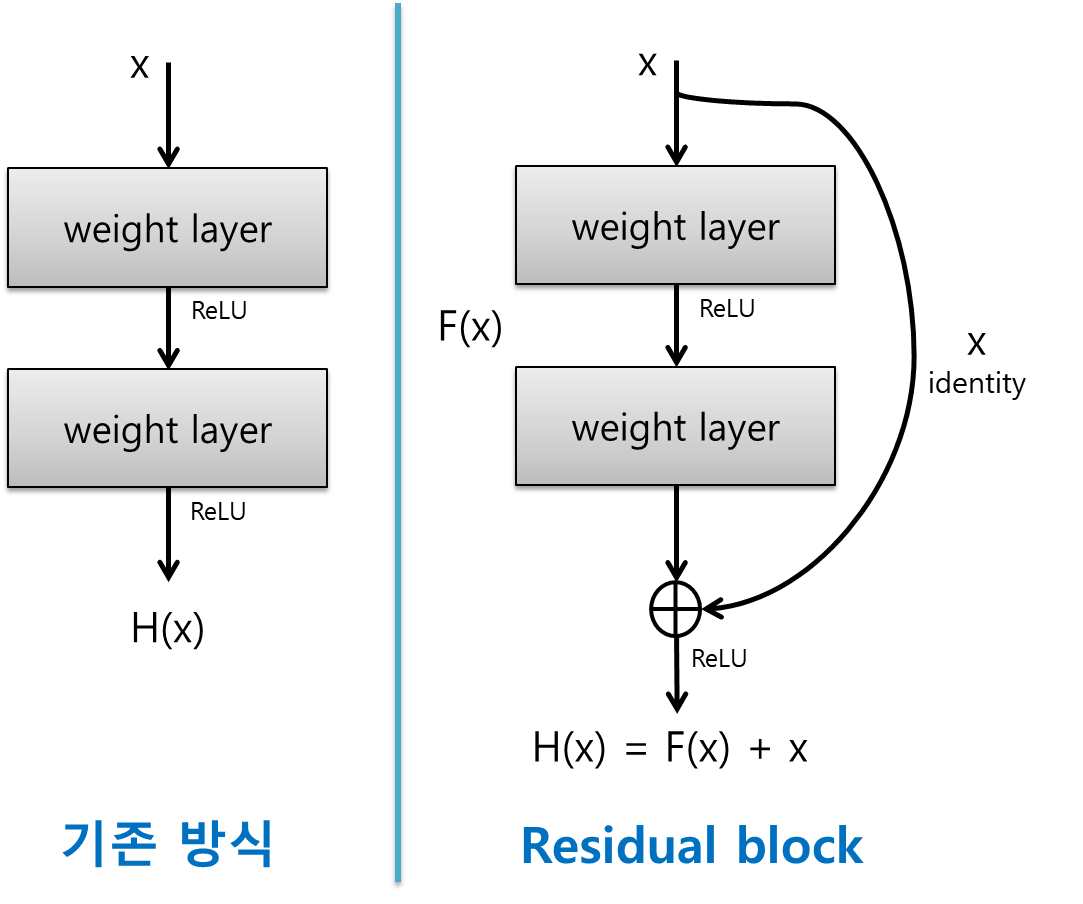
우리는 신경망을 훈련시킬 때 목적함수(F(x))를 모델링하는 것이 목표이다. 만약 입력 x를 네트워크의 출력에 더한다면(즉, 스킵 연결을 추가하면), 네트워크는 F(x)대신 H(x)=F(x)-x를 학습하게 될 것이다. 이를 잔차 학습(Residual learning)이라고 한다.
일반적인 신경망을 초기화할 때는 가중치가 0에 가깝기에 네트워크도 0에 가까운 값을 출력한다. 그러나 스킵 연결을 추가하면 이 네트워크는 입력과 같은 값을 출력한다. 즉, 초기에는 항등 함수(identity function)을 모델링한다. 목적 함수가 항등 함수에 매우 가깝다면, 훈련 속도가 매우 빨리질 것이다.
또한 스킵 연결을 많이 추가하면 일부 층이 아직 학습되지 않았더라도 네트워크는 훈련을 시작할 수 있다. 즉, 스킵 연결 덕분에 입력 신호가 전체 네트워크에 손쉽게 영향을 미친다. 심층 잔차 네트워크는 스킵 연결을 가진 작은 신경망인 잔차 유닛(Residual Unit)을 쌓은 것이다.
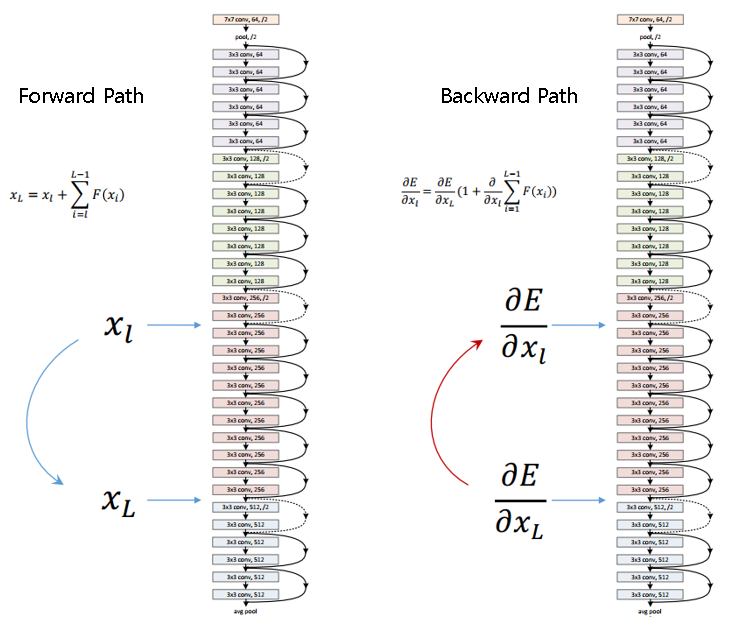
구조는 간단하다. 드랍아웃 층을 제외하면, GoogLeNet과 똑같이 시작하고 종료한다. 그러나 중간에 단순한 잔차 유닛을 매우 깊게 쌓은 것이다. 각 잔차 유닛은 배치 정규화(Batch Normalization)과 ReLU, 3X3 커널을 사용하고 공간 정보를 유지하는(스트라이드1, "same"패딩) 두 개의 합성곱 층으로 이루어져 있다.
14.4.6 Xception
GoogLeNet 구조의 변종인 모델이다. 대규모 비전 문제에서 Inception-v3 보다 훨씬 성능이 뛰어나며, GoogLeNet과 ResNet의 아이디어를 합쳤지만, 인셉션 모듈은 깊이별 분리 합성곱 층(Depthwise separable convolution layer)라는 층으로 대체하였다. 일반적인 합성곱 층이 공간상의 패턴(예를 들어 타원 형태)과 채널 사이의 패턴(예를 들어 입+눈+코=얼굴)을 동시에 잡기 위하여 필터를 사용한다. 분리 합성곱 층은 공간 패턴과 채널 사이 패턴을 분리하여 모델링 할 수 있다고 가정한다. 이 층은 두 개의 부분으로 구성되는데, 첫 번째 부분은 하나의 공간 필터를 각 입력 특성 맵에 적용하고, 두 번째 부분에서는 채널 사이 패턴만 조사한다. 이 부분은 1X1필터를 사용한 일반적인 합성곱 층이다.
분리 합성곱 층은 일반 합성곱 층보다 파라미터, 메모리, 연산을 더 적게 사용하고 일반적으로 성능은 더 높다. 그러나 분리 합성곱 층은 입력 채널마다 하나의 공간 필터만 가지기 때문에 입력층과 같이 채널이 너무 적은 층 다음에 사용하는 것은 피해야 한다.
14.4.7 SENet
이는 인셉션 네트워크와 ResNet같은 기존 구조를 확장하여 성능을 높인 모델이다. 이는 원래 구조에 있는 모든 유닛에 SE블록이라는 작은 신경망을 추가하여 성능을 향상했다.
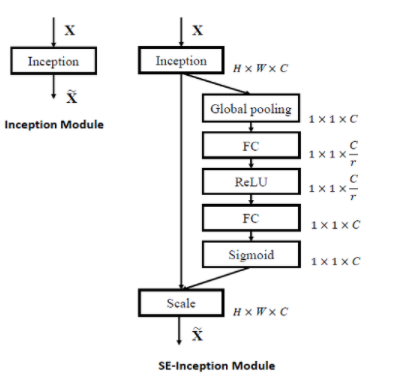
SE블록이 추가된 부분의 유닛의 출력을 깊이 차원에 초점을 맞추어 분석한다. 어떤 특성이 일반적으로 동시에 가장 크게 활성화되는지 학습한다. 그 다음 이 정보를 사용하여 특성 맵을 보정한다. 하나의 SE블록은 3개의 층으로 구성된다. 이는 전역 평균 풀링 층과 ReLU활성화 함수를 사용하는 밀집 은닉층, 시그모이드 활성화 함수를 사용하는 밀집 출력 층이다.
14.5 케라스를 사용해 ResNet-34 CNN 구현하기
ResNet-34 모델을 구현하기 위해서는 먼저 ResidualUnti층을 만들어야 한다.
cs
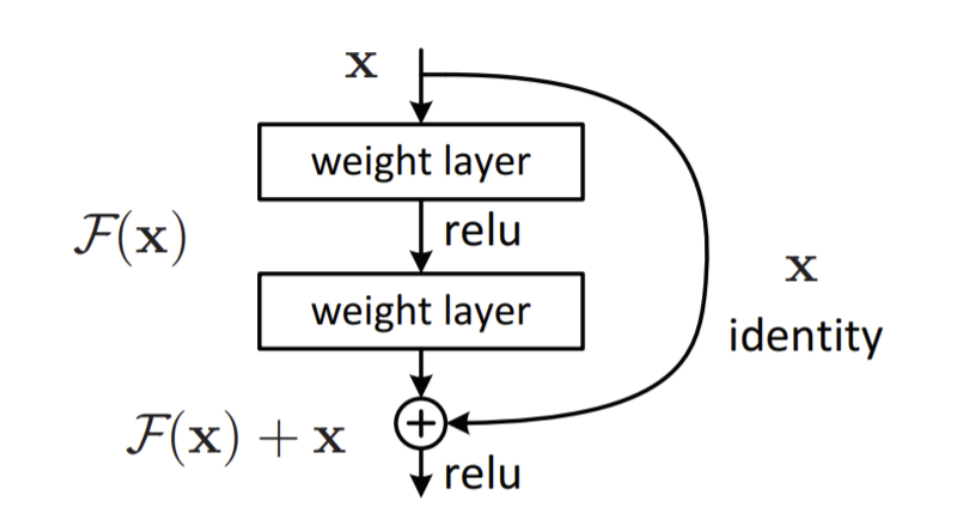
먼저 생성자에서 필요한 층을 만든다. Main layers가 이 그림의 왼쪽 모듈이며, Skip_layers는 오른쪽 모듈이다. call()메서드에서 입력을 main_layer와 skip_layers에 통과시킨 후 두 출력을 더하여 활성화 함수를 적용한다. 이때, skip layer는 스트라이드가 1보다 큰 경우에만 필요하다. 이 네트워크는 연속되어 길게 연결된 층이기 떄문에 Sequential 클래스를 사용하여 모델을 만든다.
cs
여기서 for 문은 모델에 ResidualUnit층을 더하는 반복 루프이다. 청므 3개 RU는 64개의 필터를 가지고, 그 다음 4개 RU는 128개의 필터를 가지는 식이다. 필터 개수가 이전 RU와 동일할 경우는 스트라이드를 1로 설정하거나 아니면 2로 설정하게 되고, 이후 마지막에 prev_filters를 업데이트 한다.
14.6 케라스에서 제공하는 사전훈련된 모델 사용하기
keras.applications 패키지에 있는 사전훈련된 모델을 코드 한 줄로 불러올 수 있다. 다음은 이미지넷 데이터넷에서 사전훈련된 ResNet-50 모델을 로드하는 과정이다.
cs
이때 사전훈련된 모델을 사용하려면 이미지가 적절한 크기인지 확인해야 한다. 이때 이미지의 크기가 다르면 tf.image.resize()함수로 적재한 이미지의 크기를 바꿀 수 있다.
cs
사전훈련된 모델은 이미지가 적절한 방식으로 전처리되었다고 가정한다. 경우에 따라 0에서 1사이 또는 -1에서 1사이의 입력을 기대하므로 이를 위해 모델마다 이미지를 전처리 해주는 preprocess_input()함수를 제공한다. 이 함수는 픽셀값이 0에서 255사이라고 가정하기에 바뀐 이미지 입력을 다시 바꾸어야 하기 때문에 image_resized에 255를 곱한다.
cs
이제 사전 훈련된 모델을 사용하여 예측을 수행한다.
cs
각 이미지에 대해 최상위 K개의 예측을 담은 리스트를 반환한다. 이때, 각 예측은 클래스 아이디, 이름, 확률을 포함하는 튜플이다.
cs
14.7 사전훈련된 모델을 사용한 전이 학습
충분하지 않은 훈련 데이터로 이미지 분류기를 훈련하려면 사전훈련된 모델의 하위층을 사용하는 것이 좋다. 이에 대한 예시를 들어보기 위하여 사전 훈련된 Xception 모델을 사용하여 꽃 이미지를 분류하는 모델을 훈련해보자.
이때, 먼저 데이터를 적재한 후, tfds.Split.TRAIN.subsplit함수를 이용하여 데이터셋을 나눈다.
cs
이후 이미지를 전처리해야 한다. 이CNN 모델은 224X224 크기 이미지를 기대하므로 크기를 조정해야 한다.
cs
훈련 세트를 섞은 후, 이 전처리 함수들을 데이터셋에 모두 적용하고 배치 크기를 지정하고 프리페치를 적용. 이때 tf.image.random.crop()등을 이용해 데이터 증식 가능
cs
그 다음 이미지넷에서 사전훈련된 Xception 모델 로드. 이때 include_top=False로 지정하여 네트워크의 최상층에 해당하는 전역 평균 풀링 층과 밀집 출력 층은 제외시킨다. 이때, 훈련 초기에는 사전훈련된 층의 가중치를 동결.
cs
이때, 검증 정확도가 어느정도 선에 머물러서 더 나아지지 않는다면 모든 층의 가중치 동결을 해제하고 훈련. 이떄는 사전훈련된 가중치가 훼손되는 것을 피하기 위해 훨씬 작은 학습률을 사용한다.
cs
14.8 분류와 위치 추정
물체의 위치를 추정하는 것은 회귀 작업으로 나타낼 수 있다. 물체 주위의 바운딩 박스를 예측하는 일반적인 방법은 물체 중심의 수평, 수직 좌표와 높이, 너비를 예측하는데, 즉 네 개의 숫자를 예측해야 한다. 이에 네 개의 유닛을 가진 두 번째 밀집 출력 층을 추가하고 MSE 손실을 사용해 훈련
cs
이때 레이블이 없는 데이터가 있을 수 있다. 레이블을 만드는 것은 머신러닝 프로젝트에서 가장 어렵고 비용이 많이 드는 작업이다. 이때, 이미지에 바운딩 박스를 추가하기 위한 다양한 레이블 도구가 존재하기도 하다. 또한 크라우드소싱 플랫폼 역시 고려할만 하다.
모든 이미지에 대해 바운딩 박스가 준비되었다면 클래스 레이블, 바운딩 박스와 함께 전처리된 이미지의 배치가 하나의 원소인 데이터셋을 만들어야 한다. 각 원소는(Images,(class_labels,bounding_boxes))형태의 튜플이 된다.
이때, 회귀 문제이므로 MSE를 손실 함수로 사용할 수 있으나 바운딩 박스에 관하여는 좋은 지표는 아니므로 IoU를 사용해야 한다. 이는 바운딩 박스와 타깃 바운딩 박스 사이에 중첩되는 영역을 전체 영역으로 나눈 것이다. tf.keras.metrics.MeanIoU로 사용 가능하다.
14.9 객체 탐지
하나의 이미지에서 여러 물체를 분류하고 위치를 추정하는 작업을 객체 탐지라고 한다. 이전까지 널리 사용되던 방법은 하나의 물체를 분류하고 위치를 찾는 분류기를 훈련한 다음 이미지를 훑는 것. 이 방식은 매우 쉽지만 조금씩 다른 위치에서 동일한 물체를 여러 번 감지할 수 있어, 불필요한 바운딩 박스를 제거하기 위해 사후 처리가 필요하다. 이를 위한 방법은 NMS이다.
그러나 이러한 방법보다, 완전 합성곱 신경망(fully convolutional network,FCN)을 사용하면 훨씬 빠르게 이미지에 슬라이딩 할 수 있다.
14.9.1 완전 합성곱 신경망
CNN맨 위의 밀집 층을 합성곱 층으로 바꿀 수 있다고 하는 방법론을 제시한 것. 이러한 방식을 거치면 밀집 층은 입력 특성마다 하나의 가중치를 두므로 특정 입력 크기를 기대하지만 합성곱 층을ㄴ 어떤 크기의 이미지도 처리할 수 있다. 대신 합성곱 층은 입력 채널마다 커널 가중치가 달라서 특정 개수의 채널을 기대한다. 결국, FCN은 합성곱 층과 동일한 성질을 가진 풀링 층만 가지므로 어떤 크기의 이미지에서도 훈련하고 실행할 수 있게 된다. 또한 딱 한 번만 이미지를 처리하기 때문에 더욱 효율적이다(YOLO).
14.9.2 You only look once, YOLO
매우 빠르고 정확한 객체 탐지 구조. 이에 실시간으로 비디오에도 적용할 수 있다. YOLOv3은 다음과 같은 특성을 가진다.
- 각 격자 셀마다 1개가 아닌 5개의 바운딩 박스를 출력한다. 바운딩 박스마다 하나의 존재여부 점수가 부여된다.
- 바운딩 박스 중심의 절대 좌표를 예측하는 대신 격자 셀에 대한 상대 좌표를 예측한다. (0,1)은 셀의 왼쪽 위를 의미하고, (1,1)은 오른쪽 아래를 의미한다. 각 격자 셀에 대해 YOLOv3는 바운딩 박스의 중심이 격자 셀 안에 놓은 것만을 예측하도록 훈련된다. 물론 바운딩 박스 자체는 격자 셀 밖으로 넘어갈 수 있다. YOLOv3는 로지스틱 활성화함수를 적용하여 바운딩 박스 좌표가 0과 1사이가 되도록 만든다.
- 신경망을 훈련하기 전 앵커박스(또는 사전 바운딩 박스)라 부르는 5개의 대표 바운딩 박스 크기를 찾는다. 이를 위해 k-mean 알고리즘을 훈련 세트 바운딩 박스의 높이와 너비에 적용한다. 이를 통하여 네트워크는 적절한 차원의 바운딩 박스를 예측할 가능성이 높으며, 적합한 바운딩 박스로 보이는 것을 빠르게 학습할 수 있기에 훈련 속도를 높여준다.
- 네트워크가 다른 스케일을 가진 이미지를 사용하여 훈련하고, 훈련하는 동안 몇 번의 배치마다 랜덤하게 새로운 이미지 차원을 선택한다(330X330에서 608X608 픽셀까지). 이를 통해 네트워크가 다른 스케일의 객체를 감지하는 방법을 학습한다. YOLOv3을 다른 스케일에 사용할 수도 있다. 작은 스케일은 정확도가 떨어지지만 속도가 빠르다.
이 외에도 SSD와 Faster R-CNN같은 모델이 존재한다. 탐지 시스템은 속도, 정확도, 복잡도 등 여러 요인에 기반해 선택되며, 테스트 환경에 유동성이 많아 기술이 매우 빠르게 발전한다.
객체 탐지에서 널리 사용되는 평가 지표는 mAP(mean average precision)이다. 보통 객체 탐지의 지표는 정밀도와 재현율의 반비례 관계를 가지게 된다. 이에 최소 재현율에서 분류기가 제공하는 최대 정밀도를 찾아야 한다. 이에 10%, 20%에서 100%까지 재현율에서의 최대 정밀도를 계산하고, 이 최대 정밀도를 평균하는데, 이를 평균 정밀도(average precision(AP))라고 한다. 두 개 이상의 클래스가 있을 때는 각 클래스에 대해 AP를 계산한 다음 평균AP를 내는데, 이를 mAP라고 한다.
14.10 시맨틱 분할
시맨틱 분할(semantic segmentation)에서 각 픽셀은 픽셀이 속한 객체의 클래스로 분류된다(예를 들어 도로, 자동차, 보행자, 건물 등). 이때 클래스가 같은 물체는 구별되지 않는다. 이 작업에서 가장 어려운 점은 이미지가 일반적인 CNN을 통과할 때 점진적으로 위치 정보를 잃는 것이다(1 이상의 스트라이드를 사용하는 층 때문에).
이를 해결하기 위한 방법을 위해서는 먼저 CNN을 FCN으로 변환한다. 이때 이 CNN이 입력 이미지에 적용하는 전체 스트라이드는 32이다(1보다 큰 스트라이드를 모두 더한 것). 이는 마지막 층이 입력 이미지보다 32배나 작은 특성 맵을 출력한다는 것인데, 이러면 너무 듬성듬성 해지므로 해상도를 32배로 늘리는 업샘플링 층(upsampling layer)를 하나 추가한다.
업생플링을 위한 방법으로는 이중 선형 보간이나 전치 합성곱 층 등이 존재한다. 이때, 여기서 이 방법에서 사용된 전치 합성곱 층은 Conv2DTrasnpose를 이용하여 사용 가능하다. 이를 개선하기 위해 저자들은 아래쪽 층에서부터 스킵 연결을 추가했다. 이 방식으로 풀링 층에서 잃은 일부 공간 정보를 복원하고, 비슷하게 두 번째 스킵 연결을 사용해 더 낮은 층의 세부 정보를 복원하여 최상의 구조를 만든다. 이러한 방법으로 이미지의 해상도를 증가시킬 수 있으며, 이를 초해상도라고 부른다.
텐서플로 모델 프로젝트에서 사전훈련된 인스턴스 분할모델은 시맨틱 분할과 비슷하지만, 동일한 클래스 물체를 하나의 덩어리로 합치는 것이 아닌 각 물체를 구분하여 표시한다. 이는 Faster R-CNN을 확장하여 각 바운딩 박스에 대해 픽셀 마스크를 추가한 Mask R-CNN을 통하여 제안되었다. 따라서 물체마다 클래스 추정 확률과 바운딩 박스를 얻는 것뿐만 아니라 바운딩 박스 안에 들어 있는 물체의 픽셀을 구분하는 픽셀 마스크도 얻을 수 있다.
컴퓨터 비전 분야에는 적대적 학습(adversarial learning), 설명 가능성(explainability), 현실같은 이미지 생성(image generation), 객체를 한 번 본후 인식할 수 있는 시스템인 싱글-샷 학습(single-shot learning) 등이 연구되고 있다.
텐서플로의 합성곱 연산에는 다음과 같은 것이 제공된다.
- keras.layers.Conv1D: 1D입력에 대한 합성곱 층 만든다
- keras.layers.Conv3D: 3D입력을 위한 합성곱 층
- dilation_rate: tf.keras의 합성곱 층에 있는 dilation_rate 매개변수를 2 이상으로 지정하였을 때 아트루스 합성곱 층(atrous convolution layer)가 된다. 이는 0으로 된 행과 열을 추가하여 늘린 필터로 보통의 합성곱 층을 사용하는 것과 동일하다.
- tf.nn.depthwise_conv2d(): 깊이방향 합성곱 층(depthwise convolution layer)를 만드는데 쓰인다. 모든 필터를 개개의 입력 채널에 독깁적으로 적용하여, f_n개의 필터와 f'_n개의 채널이 있다면 f_n*f'_n개의 특성 맵을 출력한다.
