Hands-On Machine Learning Chapter 2 머신러닝 프로젝트 처음부터 끝까지

JINU·2021년 9월 17일
0

Hands-On Machine Learning

목록 보기
2/5
post-thumbnail
post-custom-banner

진행 순서

1. 큰 그림을 본다.
2. 데이터를 구한다.
3. 데이터로부터 통찰을 얻기 위해 탐색하고 시각화한다.
4. 머신러닝 알고리즘을 위해 데이터를 준비한다.
5. 모델을 선택하고 훈련시킨다.
6. 모델을 상세하게 조정한다.
7. 솔루션을 제시한다.
8. 시스템을 론칭하고 모니터링하고 유지 보수한다.

2.1 실제 데이터로 작업하기

2.2 큰 그림 보기

2.2.1 문제 정의

가장 먼저 해야하는 것은 '비즈니스의 목적 정확히 설정'. 우리의 목표는 모델을 만드는 것이 아니라, 이 모델을 이용하여 어떻게 이익을 얻을까 이다. 목적을 아는 것은 문제를 어떻게 구성할지, 어떤 알고리즘을 선택할지, 모델 평가에 어떤 성능 지표를 사용할지, 모델 튜닝을 위해 어떤 노력을 할지를 결정하게 된다.

다음으로 해야하는 것은 '현재 솔루션은 어떻게 구성되어 있나'이다. 현재 상황은 문제 해결 방법에 대한 정보는 물론이고 참고 성능으로도 사용할 수 있다.

이제, 이러한 정보들을 가지고 시스템을 설계해야 하는데, 먼저 문제를 정의해야 한다. 이는 지도 학습, 비지도 학습, 강화 학습 중 무엇을 사용해야 하며, 분류나 회귀인가, 어떤 작업인가, 배치 학습과 온라인 학습 중 어느 것을 사용해야 할까 설정해야 함.

레이블된 훈련 샘플이 있으면 전형적인 지도 학습이며, 값을 예측해야 하는 경우는 회귀 문제에 각 구역마다 하나의 값을 예측하는 경우 단변량 회귀를, 각 구역마다 여러 값을 예측한다면 다변량 회귀 문제이다. 마지막으로 시스템에 들어오는 데이터가 연속적인 흐름이 없으면 배치 학습이 적절하다.

파이프라인

데이터 처리 컴포넌트(component)들이 연속되어 있는 것을 데이터 파이프라인(Pipeline)이라고 한다. 머신러닝 시스템은 데이터를 조작하고 변환할 일이 많아 파이프라인을 사용하는 일이 매우 흔하다.

보통 컴포넌트들은 비동기적으로 동작한다. 각 컴포넌트는 많은 데이터를 추출해 처리하고 그 결과를 다른 데이터 저장소로 보낸다. 그러면 일정 시간 후 파이프라인의 다음 컴포넌트가 그 데이터를 추출해 자신의 출력 결과를 만든다. 즉, 각 컴포넌트는 완전히 독립적이고, 컴포넌트 사이의 인터페이스는 데이터 저장소 뿐이다. 이는 시스템을 이해하기 쉽게 만들고, 각 팀은 각자의 컴포넌트에 집중 할 수 있게한다. 이에 한 컴포넌트가 고장나더라도 하위 컴포넌트는 문제가 생긴 컴포턴트의 마지막 출력을 사용해 한동안은 평상시와 같이 계속 동작할 수 있다.

그러나, 계속 모니터링이 적절히 되지 않으면 고장 난 컴포턴트를 한동안 모를 수 있고, 데이터가 만들어진지 오래 되면 전체 시스템의 성능이 떨어진다.

2.2.2 성능 측정 지표 선택

다음으로는 성능 측정 지표를 선택해야 한다. 회귀 문제에서는 포통 평균 제곱근 오차(RMSE)를 사용한다.

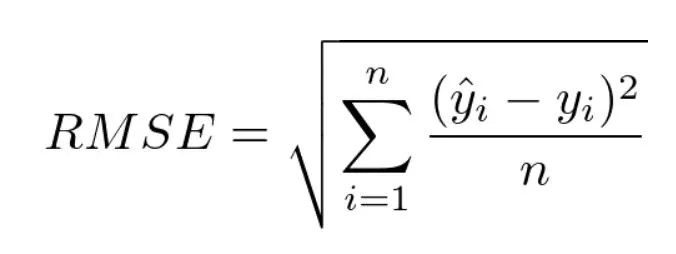
그러나, 이상치를 보이는 구역이 많다고 가정하였을 때는 평균 절대 오차(MAE)를 사용하는 것이 더 좋을 수 있다.

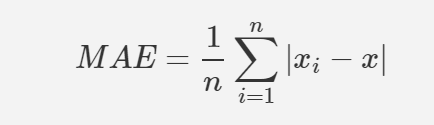
이때, RMSE와 MAE 모두 예측값의 벡터와 타깃값의 벡터 사이의 거리를 재는 방법. 거리 측정에는 여러 가지 방법(또는 Norm)이 가능하다.

  • 제곱항을 합한 것의 제곱근(RMSE)계산은 유클리디안 norm에 해당한다. l2-norm이라고도 한다.

  • 절대값의 합을 계산하는 것은 l1-norm에 해당한다. 이는 도시의 구획이 직각으로 나뉘어 있을 때 이 도시의 두 지점 사이의 거리를 측정하는 것과 같아 맨해튼 norm이라고도 한다.

  • 일반적으로 원소가 n개인 벡터v의 lk-norm은 이렇게 정의한다. l0은 단순히 벡터에 있는 0이 아닌 원소의 수이고, l-infinite는 벡터에서 가장 큰 절댓값이 된다.

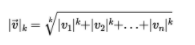
  • norm의 지수가 클수록 큰 값의 원소에 치우치며, 작은 값은 무시된다. 그래서 RMSE가 MAE보다 조금 더 이상치에 민감하지만, 종 모양 분포의 양 끝단처럼 이상치가 매우 드물면 RMSE가 더 좋은 선택이 될 것이다.

2.2.3 가정 검사

마지막으로, 지금 까지 만든 가정을 나열하고 검사해봐야 한다. 이 과정에서 심각한 문제를 일찍 발견할 수도 있다. 우리는 올바른 카테고리를 구축하는 것이 목표이기 때문에, 혹시나 다른 카테고리가 들어가 버리면 모델에 심각한 문제가 발생할 수 있다.

2.3 데이터 가져오기

2.3.1 작업환경 만들기

2.3.2 데이터 다운로드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import os
import tarfile
import urllib.request
 
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/rickiepark/handson-ml2/master/"
HOUSING_PATH = os.path.join("datasets", "housing")
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"
 
def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH):
    if not os.path.isdir(housing_path):
        os.makedirs(housing_path)
    tgz_path = os.path.join(housing_path, "housing.tgz")
    urllib.request.urlretrieve(housing_url, tgz_path)
    housing_tgz = tarfile.open(tgz_path)
    housing_tgz.extractall(path=housing_path)
    housing_tgz.close()
cs
fetch_housing_data()를 호출하면 현재 작업공간에 datasets/housing 디렉터리를 만들고 housing.tgz 파일을 내려받고 같은 디렉터리에 압축을 풀어 housing.csv파일 만든다.
1
2
3
4
5
6
7
8
9
10
11
fetch_housing_data()
 
 
import pandas as pd
 
def load_housing_data(housing_path=HOUSING_PATH):
    csv_path = os.path.join(housing_path, "housing.csv")
    return pd.read_csv(csv_path)
 
housing = load_housing_data()
housing.head()
cs
이를 통해 데이터의 처음 다섯 행 확인.

이 외에도 다음과 같은 메서드로 데이터 정보 확인 가능

  • info()메서드를 통해 데이터에 대한 간략한 설명과 특히 전체 행 수, 각 특성의 데이터 타입과 null이 아닌 값의 개수를 확인.

  • 어떤 카테고리가 있고, 각 카테고리마다 얼마나 많은 구역이 있는지 value_counts()메서드를 통하여 확인.

  • describe()를 통해 숫자형 특성의 요약 정보를 볼 수 있다.

데이터의 각 숫자형 특성을 히스토그램으로 그려볼 수도 있다.

1
2
3
4
5
%matplotlib inline
import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(20,15))
save_fig("attribute_histogram_plots")
plt.show()
cs

이때, 우리는 데이터를 더 깊게 들여다보기 전에 Test set을 떼어 놓아야 한다.

2.3.4 테스트 세트 만들기

우리는 모델을 학습시키기 전에 Test set을 따로 떼어놓아야 한다. 만약 Test set으로 일반화 오차를 추정하면 매우 낙관적인 추정이 되며 시스템을 론칭하였을 때 기대한 성능이 나오지 않을 것이다. 이를 Data snooping편향이라고 한다.

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
 
# 예시로 만든 것입니다. 실전에서는 사이킷런의 train_test_split()를 사용하세요.
def split_train_test(data, test_ratio):
    shuffled_indices = np.random.permutation(len(data))
    test_set_size = int(len(data) * test_ratio)
    test_indices = shuffled_indices[:test_set_size]
    train_indices = shuffled_indices[test_set_size:]
    return data.iloc[train_indices], data.iloc[test_indices]
 
train_set, test_set = split_train_test(housing, 0.2)
len(train_set)
cs

물론, 이 과정도 완벽하지는 않다. 프로그램을 다시 실행하면 다른 테스트 세트가 생성되고, 이를 여러 번 반복하면 모델이 전체 데이터셋을 보는 것이므로 이러한 상황은 피해야 한다. 이를 위해서는 다음과 같은 해결책이 있다.

  • 처음 실행 때 테스트 세트를 저장하고 다음번 실행에서 이를 불러들이는 것

  • 항상 같은 난수 인덱스가 생성되도록 np.random.permutation()을 호출하기 전 난수 발생기의 초깃값을 지정하는 것. 이때 다음을 많이 사용. 42에는 특별한 의미는 없지만, 이를 사용한다.

    1
    np.random.seed(42)
    		cs

그러나 이 두 방법 모두 다음번에 업데이트된 데이터 셋을 사용하려면 문제가 된다. 데이터 셋을 업데이트한 후에도 안정적인 훈련/테스트 분할을 위한 일반적인 해결책은 샘플의 식별자를 사용하여 테스트 세트로 보낼지 말지 정하는 것. 예를 들어, 샘플마다 식별자의 해시값을 계산하여 해시 최댓값의 20%보다 작거나, 같은 샘플만 테스트 세트로 보낼 수 있는데, 이렇게 하면 여러 번 반복 실행되면서 데이터셋이 갱신되더라도 테스트 세트가 동일하게 유지될 것이다.

1
2
3
4
5
6
7
8
9
from zlib import crc32
 
def test_set_check(identifier, test_ratio):
    return crc32(np.int64(identifier)) & 0xffffffff < test_ratio * 2**32
 
def split_train_test_by_id(data, test_ratio, id_column):
    ids = data[id_column]
    in_test_set = ids.apply(lambda id_: test_set_check(id_, test_ratio))
    return data.loc[~in_test_set], data.loc[in_test_set]
cs
1
2
3
4
5
6
housing_with_id = housing.reset_index()   # `index` 열이 추가된 데이터프레임을 반환합니다
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "index")
 
 
housing_with_id["id"] = housing["longitude"] * 1000 + housing["latitude"]
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "id")
cs
이는 주택 데이터인데, 주택 데이터에는 식별자 컬럼이 없으므로 행의 인덱스를 ID로 사용한다. 행의 인덱스를 사용할 때 새 데이터는 데이터셋의 끝에 추가되어야 하고, 어떤 행도 삭제되지 않아야 한다. 이것이 불가능할 땐, 고유 식별자를 만드는데 안전한 특성을 사용해야 한다.

사이킷런은 데이터셋을 여러 서브셋으로 나누는 다양한 방법을 제공한다. 가장 간단한 함수로는 train_test_split이 있는데 이는 split_train_test와 비슷하지만 난수 초깃값을 설정할 수 있는 random_state 매개변수와, 행의 개수가 같은 여러 개의 데이터셋을 넘겨서 같은 인덱스를 기반으로 나눌 수 있다.

1
2
3
from sklearn.model_selection import train_test_split
 
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
cs

지금까지는 순수한 무작위 샘플링 방식이었는데, 이는 데이터셋이 충분히 근 경우에는 일반적으로 괜찮지만 그렇지 않다면 샘플링 편향이 생길 것이다. 이를 막기 위해서는 계층적 샘플링(stratified sampling) 등이 잘 되어야 한다. 계층을 나누는 방법은 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
housing["income_cat"] = pd.cut(housing["median_income"],
                               bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
                               labels=[1, 2, 3, 4, 5])
 
from sklearn.model_selection import StratifiedShuffleSplit
 
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(housing, housing["income_cat"]):
    strat_train_set = housing.loc[train_index]
    strat_test_set = housing.loc[test_index]
 
for set_ in (strat_train_set, strat_test_set):
    set_.drop("income_cat", axis=1, inplace=True)
cs

마지막 2줄의 코드는 income_cat 특성을 삭제하여 데이터를 원래 상태로 되돌리는 것

2.4 데이터 이해를 위한 탐색과 시각화

이때, 테스트 세트를 떼어놓았는지 확인 하고 훈련 세트에 대해서만 탐색. 훈련 세트가 매우 크면 조작을 간단하고 빠르게 하기 위해 탐색을 위한 세트를 별도로 샘플링할 수도 있다. 훈련 세트를 손상키기지 않기 위해 먼저 복사본을 만든다.

1
housing = strat_train_set.copy()
cs

2.4.1 지리적 데이터 시각화

지리 정보(위도와 경도)가 존재하는 데이터는 모든 구역을 산점도로 만들어 데이터를 시각화 할 수 있다.

1
2
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)
save_fig("better_visualization_plot")
cs

이는 캘리포니아 지역을 나타내는 데, alpha 옵션을 0.1로 주어 데이터 포인트가 밀집된 영역을 잘 보여주도록 만든다.

다음은 주택 가격을 나타내기 위한 함수이다.

1
2
3
4
5
6
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
             s=housing["population"]/100, label="population", figsize=(10,7),
             c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
             sharex=False)
plt.legend()
save_fig("housing_prices_scatterplot")
cs

2.4.2 상관관계 조사

데이터셋이 그렇게 크지 않으므로, 모든 특성 간의 표준 상관계수(stadard correlation coefficient)를 corr()로 계산하자.

1
corr_matrix=housing.corr()
cs

이때, 상관관계는 선형적인 상관관계만을 측정한다. (x가 증가하면 y가 증가한다.) 특성 사이의 상관관계를 확인하는 다른 방법은 숫자형 특성 사이에 산점도를 그려주는 판다스의 scatter_matrix 함수를 사용하는 것이다.

1
2
3
4
5
6
7
8
9
10
11
12
from pandas.plotting import scatter_matrix
 
attributes = ["median_house_value", "median_income", "total_rooms",
              "housing_median_age"]
scatter_matrix(housing[attributes], figsize=(12, 8))
save_fig("scatter_matrix_plot")
 
 
housing.plot(kind="scatter", x="median_income", y="median_house_value",
             alpha=0.1)
plt.axis([0, 16, 0, 550000])
save_fig("income_vs_house_value_scatterplot")
cs

2.4.3 특성 조합으로 실험

데이터를 탐색하고 통찰하면서, 우리는 머신러닝 알고리즘에 주입하기 전에 정제해야 할 조금 이상한 데이터를 확인했으며, 특성 사이에 흥미로운 상관관계를 발견할 수 있다. 마지막으로 데이터를 준비하기 전에, 여러 특성의 조합을 시도해볼 수 있다. 집 값에 관련한 데이터이므로, 방 개수, 가구당 인원 수 등의 특성을 고려해볼 수 있다.

1
2
3
4
5
6
7
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"]=housing["population"]/housing["households"]
 
 
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)
cs

2.5 머신러닝 알고리즘을 위한 데이터 준비

이때, 함수를 수동으로 만들어 자동화해야 하는 이유가 있다.

  • 어떤 데이터셋에 대해서도 데이터 변환을 손쉽게 반복할 수 있다.(향후 모델 재사용 가능)

  • 향후 프로젝트에 사용할 수 있는 변환 라이브러리를 점진적으로 구축할 수 있다

  • 실제 시스템에서 알고리즘에 새 데이터를 주입하기 전에 변환시키는 데 이 함수를 사용할 수 있다.

  • 여러 가지 데이터 변환을 쉽게 시도해볼 수 있고, 어떤 조합이 가장 좋을지 확인하는데 편리하다.

이를 위해서, 원래 훈련 세트로 복원한 후, 예측 변수와 레이블을 분리한다.

1
2
housing = strat_train_set.drop("median_house_value", axis=1) # 훈련 세트를 위해 레이블 삭제
housing_labels = strat_train_set["median_house_value"].copy()
cs

2.5.1 데이터 정제

대부분 머신러닝 알고리즘은 누락된 특성을 다루지 못하므로, 이를 처리할 수 있는 함수를 만들어야 한다. 방법은 여러가지가 있다.

  • 해당 구역 제거
  • 전체 특성 삭제
  • 어떤 값으로 채우기(0, 평균, 중간값)

이는 데이터 프레임의 dropna(), drop(), fillna()메서드를 이용해 간단히 처리할 수 있다.

1
2
3
4
5
6
sample_incomplete_rows.dropna(subset=["total_bedrooms"])    # 옵션 1
 
sample_incomplete_rows.drop("total_bedrooms", axis=1)       # 옵션 2
 
median = housing["total_bedrooms"].median()
sample_incomplete_rows["total_bedrooms"].fillna(median, inplace=True) # 옵션 3
cs
이때, 옵션 3에서 저장한 중간값은 이후 테스트 세트에 누락된 값을 채워 넣어야 한다.

사이킷런의 SimpleImputer는 누락된 값을 손쉽게 다루도록 해준다. 누락된 값을 특성의 중간값으로 대체한다고 가정했을때, 다음과 같은 과정을 거친다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy="median")
# 이때, 중간값이 수치형 특성에서만 계산될 수 이기 때문에 텍스트 특성인 ocean_pproximity를 제외한 데이터 복사본을 생성해야 한다.
 
housing_num = housing.drop("ocean_proximity", axis=1)
# 다른 방법: housing_num = housing.select_dtypes(include=[np.number])
 
imputer.fit(housing_num)
 
imputer.statistics_
 
housing_num.median().values
 
X = imputer.transform(housing_num)
 
housing_tr = pd.DataFrame(X, columns=housing_num.columns,
                          index=housing_num.index)
cs

2.5.2 텍스트와 범주형 특성 다루기

대부분의 머신러닝 알고리즘은 숫자를 다루므로, 텍스트를 숫자로 변환해야 한다. 이를 위해 사이킷런의 OrdinalEncoder를 사용한다.

1
2
3
4
5
6
7
from sklearn.preprocessing import OrdinalEncoder
 
ordinal_encoder = OrdinalEncoder()
housing_cat_encoded = ordinal_encoder.fit_transform(housing_cat)
housing_cat_encoded[:10]
 
ordinal_encoder.categories_
cs

catergories_인스턴트 변수를 사용해 카테고리 목록을 얻을 수 있다. 범주형 특성마다 카테고리들의 1D배열을 담은 리스트가 반환된다.

이 방식의 문제는 머신러닝 알고리즘이 가까이 있는 두 값이 떨어져 있는 두 값보다 더 비슷하다고 생각한다는 점이다. (그러나, BAD, AVERAGE, GOOD 등 처럼 순서가 있는 경우는 괜찮다.) 이러한 문제는 카테고리별 이진 특성을 만들어서 해결할 수 있다. 카테고리가 '<1H OCEAN>'일 때 한 특성이 1이고(그 외 특성은 0), 카테고리가 'ISLAND'일때 다른 한 특성은 1이 되는(그 외는 0) 방법을 사용. 이를 원-핫 인코딩이라고 부른다.

1
2
3
4
5
6
7
from sklearn.preprocessing import OneHotEncoder
 
cat_encoder = OneHotEncoder()
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_1hot
 
housing_cat_1hot.toarray()
cs

이때 출력은 넘파이 배열이 아닌 사이파이의 희소 행렬 인데, 이는 수천 개의 카테고리가 있는 범주형 특성일 경우 매우 효율적이다. 0을 모두 메모리에 저장하는 것은 낭비이므로, 희소 행렬은 0이 아닌 원소의 위치만 저장한다. 이 행렬을 거의 일반적인 2차원 배열처럼 사용할 수 있지만, toarray()를 통해 밀집된 넘파이 배열로 바꿀 수 있다.

카테고리의 수가 많다면, 원-핫 인코딩은 훈련을 느리게 하고 성능을 감소시킬 수 있다. 이는 임베딩이라 부르는 학습 가능한 저차원 벡터로 바꿀 수 있다.

2.5.3 나만의 변환기

사이킷런이 유용한 변환기를 많이 제공하지만, 특별한 정제 작업이나 어떤 특성들을 조합하는 등의 작업을 위해 자신만의 변환기를 만들어야 할 때가 있다. 이때, 내가 만든 변환기를(파이프라인과 같은) 사이킷런의 기능과 연동해야 한다. 이때 사이킷런은 상속이 아닌, duck typing을 지원하므로 fit(), transform(), fit_transform() 메서드를 이용해 파이썬 클래스를 만들어야 한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from sklearn.base import BaseEstimator, TransformerMixin
 
# 열 인덱스
rooms_ix, bedrooms_ix, population_ix, households_ix = 3, 4, 5, 6
 
class CombinedAttributesAdder(BaseEstimator, TransformerMixin):
    def __init__(self, add_bedrooms_per_room=True): # *args 또는 **kargs 없음
        self.add_bedrooms_per_room = add_bedrooms_per_room
    def fit(self, X, y=None):
        return self  # 아무것도 하지 않습니다
    def transform(self, X):
        rooms_per_household = X[:, rooms_ix] / X[:, households_ix]
        population_per_household = X[:, population_ix] / X[:, households_ix]
        if self.add_bedrooms_per_room:
            bedrooms_per_room = X[:, bedrooms_ix] / X[:, rooms_ix]
            return np.c_[X, rooms_per_household, population_per_household,
                         bedrooms_per_room]
        else:
            return np.c_[X, rooms_per_household, population_per_household]
 
attr_adder = CombinedAttributesAdder(add_bedrooms_per_room=False)
housing_extra_attribs = attr_adder.transform(housing.to_numpy())
 
#책에서는 간단하게 인덱스 (3, 4, 5, 6)을 하드코딩했지만 다음처럼 동적으로 처리하는 것이 더 좋습니다:
 
col_names = "total_rooms", "total_bedrooms", "population", "households"
rooms_ix, bedrooms_ix, population_ix, households_ix = [
    housing.columns.get_loc(c) for c in col_names] # 열 인덱스 구하기
cs

2.5.4 특성 스케일링

데이터에 적용할 가장 중요한 변환 중 하나는 특성 스케일링(Feature scaling). 이로는 min-max 스케일링(Normalization)과 표준화(standardization)이 있다.

min-max 스케일링은 0~1 범위에 들도록 값을 이동하고 스케일을 조정하는 것. 보통 데이터에서는 최솟값을 뺀 후 최댓값과 최솟값의 차이로 나누면 이렇게 할 수 있다. 사이킷런의 MinMaxScaler 변환기를 사용하거나 feature_range를 통해 범위를 변경할 수 있다.

표준화는 먼저 평균을 뺀 후 표준편차로 나누어 결과 분포의 분산이 1이 되도록 만든다. 이는 min-max 스케일링과는 다르게 범위의 상한과 하한이 없어 어떤 알고리즘에서는 문제가 될 수 있으나, 이상치에 영향을 덜 받게 된다. 이를 위해서 사이킷런에는 StandardScaler 변환기가 존재한다.

2.5.5 변환 파이프라인

변환 단계가 많은데, 이를 정확한 순서대로 실행해야 한다. 사이킷런의 Pipeline클래스를 이용하여 연속된 변환을 순서대로 처리할 수 있다. 다음은 숫자 특성을 간단히 처리하는 파이프라인 이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
 
num_pipeline = Pipeline([
        ('imputer', SimpleImputer(strategy="median")),
        ('attribs_adder', CombinedAttributesAdder()),
        ('std_scaler', StandardScaler()),
    ])
 
housing_num_tr = num_pipeline.fit_transform(housing_num)
 
from sklearn.compose import ColumnTransformer
 
num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]
 
full_pipeline = ColumnTransformer([
        ("num", num_pipeline, num_attribs),
        ("cat", OneHotEncoder(), cat_attribs),
    ])
 
housing_prepared = full_pipeline.fit_transform(housing)
cs

2.6 모델 선택과 훈련

2.6.1 훈련 세트에서 훈련하고 평가하기

선형 회귀 모델을 훈련시킨 후, 사이킷런의 mean_square_error함수를 사용해 RMSE 측정.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from sklearn.linear_model import LinearRegression
 
lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)
 
# 훈련 샘플 몇 개를 사용해 전체 파이프라인을 적용해 보겠습니다
some_data = housing.iloc[:5]
some_labels = housing_labels.iloc[:5]
some_data_prepared = full_pipeline.transform(some_data)
 
print("예측:", lin_reg.predict(some_data_prepared))
 
from sklearn.metrics import mean_squared_error
 
housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels, housing_predictions)
lin_rmse = np.sqrt(lin_mse)
lin_rmse
cs

모델이 훈련 데이터에 과소적합 되었기에, 이를 해결하기 위해 더 강력한 모델을 선택하거나, 훈련 알고리즘에 더 좋은 특성을 주입하거나, 모델의 규제를 감소시켜야 한다. 먼저 더 강력한 모델을 사용하고자 한다.

이에 DecisionTreeRegressor를 훈련시킨다.

1
2
3
4
5
6
7
8
9
from sklearn.tree import DecisionTreeRegressor
 
tree_reg = DecisionTreeRegressor(random_state=42)
tree_reg.fit(housing_prepared, housing_labels)
 
housing_predictions = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
tree_rmse
cs

이는 오히려 오차가 전혀 없으므로, 과대적합된 것으로 보인다.

2.6.2 교차 검증을 사용한 평가

결정 트리 모델ㅇㄹ 평가하는 방법은 우선 train_test_split함수를 사용하여 훈련 세트를 더 작은 훈련 세트와 검증으로 나누고, 더 작은 훈련 세트에서 모델을 훈련 시키고 검증 세트로 모델을 평가하는 방법이 있다.

이를 보통 k-fold cross-validation기능을 통해 한다.

1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.model_selection import cross_val_score
 
scores = cross_val_score(tree_reg, housing_prepared, housing_labels,
                         scoring="neg_mean_squared_error", cv=10)
tree_rmse_scores = np.sqrt(-scores)
 
def display_scores(scores):
    print("점수:", scores)
    print("평균:", scores.mean())
    print("표준 편차:", scores.std())
 
display_scores(tree_rmse_scores)
cs

결정 트리 모델이 과대적합되어 좋은 성능을 보이지 못했으므로, RandomForestRegressor모델을 사용한다. 물론, 여러 모델을 합쳐 앙상블 학습을 할 수도 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from sklearn.ensemble import RandomForestRegressor
 
forest_reg = RandomForestRegressor(n_estimators=100, random_state=42)
forest_reg.fit(housing_prepared, housing_labels)
 
housing_predictions = forest_reg.predict(housing_prepared)
forest_mse = mean_squared_error(housing_labels, housing_predictions)
forest_rmse = np.sqrt(forest_mse)
forest_rmse
 
from sklearn.model_selection import cross_val_score
 
forest_scores = cross_val_score(forest_reg, housing_prepared, housing_labels,
                                scoring="neg_mean_squared_error", cv=10)
forest_rmse_scores = np.sqrt(-forest_scores)
display_scores(forest_rmse_scores)
cs

2.7 모델 세부 튜닝

2.7.1 그리드 탐색

가장 단순한 방법은 수동으로 하이퍼 파라미터를 조정하는 것. 사이킷런의 GridSearchCV를 이용하여 탐색하고자 하는 하이퍼파라미터와 시도해볼 값을 지정하기만 하면 된다. 그러면 가능한 모든 하이퍼파라미터 조합에 대해 교차 검증을 사용해 평가하게 된다. 다음은 RandomForestRegressor에 대한 최적의 하이퍼파라미터 조합을 탐색하는 과정이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from sklearn.model_selection import GridSearchCV
 
param_grid = [
    # 12(=3×4)개의 하이퍼파라미터 조합을 시도합니다.
    {'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]},
    # bootstrap은 False로 하고 6(=2×3)개의 조합을 시도합니다.
    {'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]},
  ]
 
forest_reg = RandomForestRegressor(random_state=42)
# 다섯 개의 폴드로 훈련하면 총 (12+6)*5=90번의 훈련이 일어납니다.
grid_search = GridSearchCV(forest_reg, param_grid, cv=5,
                           scoring='neg_mean_squared_error',
                           return_train_score=True)
grid_search.fit(housing_prepared, housing_labels)
 
grid_search.best_params_
 
grid_search.best_estimator_
#이를 통해 최적의 추정기에 직접 접근할 수 있다.
cs

평가 점수는 아래와 같이 확인할 수 있다.

1
2
3
cvres = grid_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
    print(np.sqrt(-mean_score), params)
cs

데이터 준비 단계를 하나의 하이퍼파라미터처럼 다룰 수도 있다. 예를 들어, 그리드 탐색이 확실하지 않은 특성을 추가할지 말지 자동으로 정할 수 있다. 비슷하게 이상치나 값이 빈 특성을 다루거나, 특성 선택 등을 자동으로 처리하는 데 그리드 탐색을 사용한다.

2.7.2 랜덤 탐색

이는 비교적 적은 수의 조합을 탐구할 때 괜찮으나, 하이퍼파라미터 탐색 공간이 커지면 RandomizedSearchCV를 사용하는 것이 더 좋다. 이는 GridSearchCV와 비슷하지만 가능한 모든 조합을 시도하는 대신 각 반복마다 하이퍼파라미터에 임의의 수를 대입하여 지정한 횟수만큼 평가한다. 이는 다음과 같은 장점이 있다.

  • 랜덤 탐색을 1000회 반복하도록 실행하면, 하이퍼파라미터마다 각기 다른 1000개의 값을 탐색한다.

  • 단순히 반복 횟수를 조절하는 것으로 하이퍼파라미터 탐색에 투입할 컴퓨팅 자원을 제어할 수 있다.

2.7.3 앙상블 방법

단일 모델들을 엮는 방법

2.7.4 최상의 모델과 오차 분석

최상의 결과를 낸 모델을 분석하면 문제에 대한 좋은 통찰을 얻을 수 있다. 정확한 예측을 만들기 위한 각 특성의 상대적인 중요도 등을 알 수 있다. 시스템이 특정한 오차를 만들었다면, 왜 그런 문제가 생겼는지 이해하고 문제를 해결하는 방법이 무엇인지 찾아야 한다. (추가 특성을 포함시키거나, 불필요한 특성을 제거하거나, 이상치를 제외하는 등)

2.7.5 테스트 세트로 시스템 평가하기

테스트 세트에서 최종 모델을 평가한다. 테스트 세트에서 예측변수와 레이블을 얻은 후, full_pipeline을 사용하여 데이터를 변환하고 테스트 세트에서 최종 모델을 평가한다. 이때, 아래의 scipy.stats.t.interval()을 통하여 일반화 오차 95%의 신뢰구간을 계산할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
final_model = grid_search.best_estimator_
 
X_test = strat_test_set.drop("median_house_value", axis=1)
y_test = strat_test_set["median_house_value"].copy()
 
X_test_prepared = full_pipeline.transform(X_test)
final_predictions = final_model.predict(X_test_prepared)
 
final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)
 
final_rmse
 
from scipy import stats
 
confidence = 0.95
squared_errors = (final_predictions - y_test) ** 2
np.sqrt(stats.t.interval(confidence, len(squared_errors) - 1,
                         loc=squared_errors.mean(),
                         scale=stats.sem(squared_errors)))
cs

2.8 론칭, 모니터링, 시스템 유지 보수

전체 전처리 파이프라인과 예측 파이프라인이 포함된 훈련된 사이킷런 모델을 저장하거나, 웹 애플리케이션이 REST API를 통해 질의할 수 있는 전용 웹 서비스로 모델을 감싸거나, 구글 클라우드 AI플랫폼과 같은 클라우드에 배포함으로써 이를 배포할 수 있다.

실시간으로 시스템의 성능을 체크하고 성능이 떨어졌을 때 알람을 통지할 수 있는 모니터링 코드를 작성해야 한다. 데이터가 계속 변화하면 데이터셋을 업데이트하고 모델을 정기적으로 다시 훈련해야 하며, 전체 과정에서 가능한 많은 것을 자동화해야 한다.

profile
JINU
이전 포스트

Hands-On Machine Learning Chapter 1 한눈에 보는 머신러닝

다음 포스트

Hands-On Machine Learning Chapter 12 텐서플로를 사용한 사용자 정의 모델과 훈련

post-custom-banner

0개의 댓글