Hands-On Machine Learning Chapter 12 텐서플로를 사용한 사용자 정의 모델과 훈련

12.1 텐서플로 훑어보기

텐서플로는 강력한 수치 계산용 라이브러리. 특히 대규모 머신러닝에 잘 맞도록 튜닝 되어 있다. 또한 계산량이 많은 어떠한 작업에도 사용할 수 있다. 텐서플로의 핵심은 다음과 같다.

• 핵심구조는 numpy와 비슷하지만 GPU를 지원한다.

• 여러 장치와 서버에 대해서 분산 컴퓨팅을 지원한다.

• 일종의 JIT(JustInTime) 컴파일러를 포함한다. 속도를 높이고 메모리 사용량을 줄이기 위해 계산을 최적화 한다. 이를 위해 파이썬 함수에서 계산 그래프를 추출한 다음 최적화 한 후, 효율적으로 실행.

• 계산 그래프는 플랫폼에 중립적인 포맷으로 내보낼 수 있다.

• 텐서플로는 자동 미분기능과 RMSProp, Nadam과 같은 고성능 옵티마이저를 제공한다.

텐서플로는 이 외에도 다양한 파이썬 API를 제공한다.

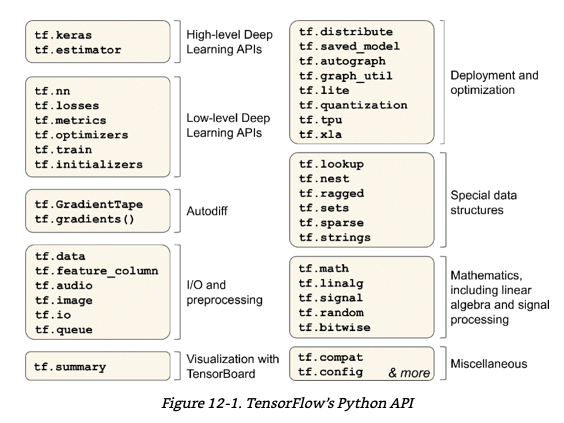
많은 연산은 커널(kernel)이라 부르는 여러 구현을 가진다. 각 커널은 CPU, GPU, TPU와 같은 특정 장치에 맞추어 만들어졌다. GPU는 게산을 작은 단위로 나누어 여러 GPU쓰레드에서 병렬로 실행하므로 속도를 극적으로 향상 시킵니다. TPU는 딥러닝 연산을 위해 특별하게 설계된 하드웨어이다.

텐서플로는 윈도우, 리눅스, 맥 os 뿐만 아니라 iOS와 안드로이드 같은 모바일 장치에서도 실행가능하다.

텐서플로는 광범위한 라이브러리 생태계를 가지고 있는데, 그 중 유용한 것은 시각화를 위한 텐서보드(TensorBoard)와 텐서플로 제품화를 위한 라이브러리 모음인 TFX(TensorFlow Extended)가 있다. 여기에는 데이터 시각화, 전처리, 모델 분석, 서빙 등이 포함된다. 또한 구글의 텐서플로 허브(TensorFlow Hub)를 사용하면 사전 훈련된 신경망을 손쉽게 다운로드 하여 재사용 가능.

12.2 넘파이처럼 텐서플로 사용하기

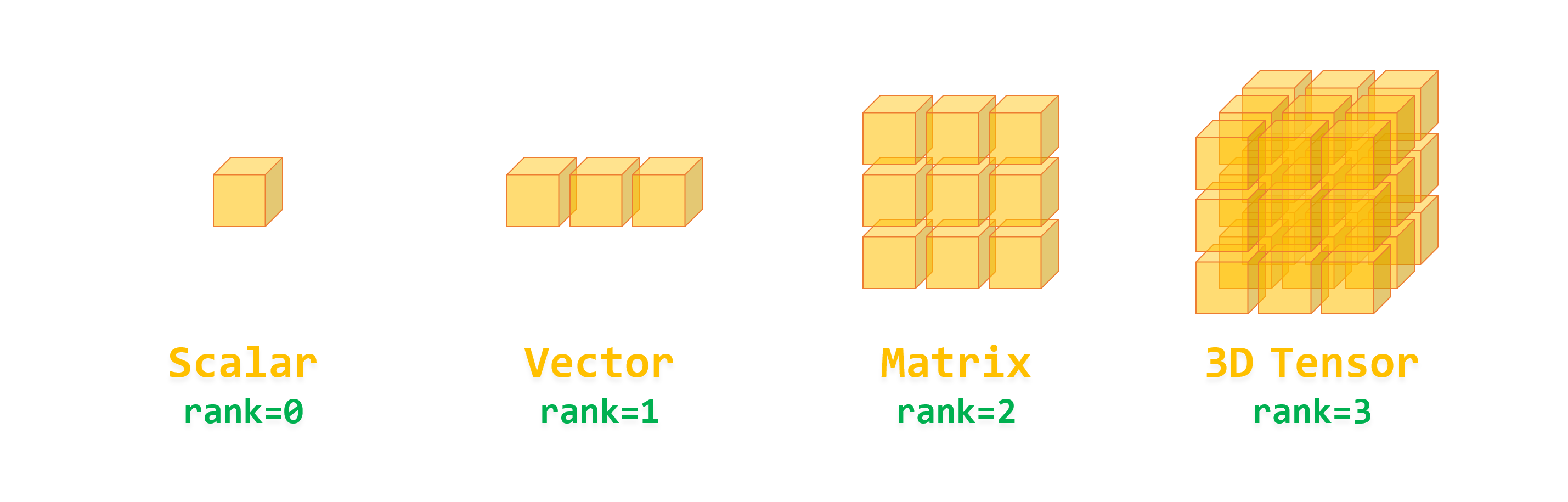
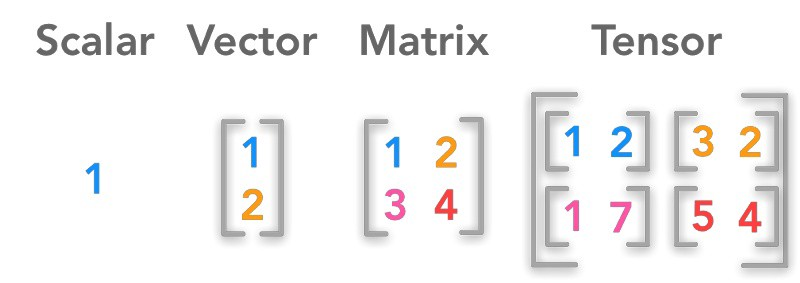
텐서플로 API는 Tensor를 순환시킨다. 텐서는 한 연산에서 다른 연산으로 흐르기 때문에 TensorFlow라고 부르는 것. 텐서는 일반적으로 다차원 배열이지만 스칼라 값도 가질 수 있다.

12.2.1 텐서와 연산

tf.constant()함수로 텐서를 만들 수 있다. 다음은 2개의 행과, 3개의 열을 가지는 실수 행렬을 나타내는 텐서를 만드는 코드와 실행 결과

1

tf.constant([[1., 2., 3.], [4., 5., 6.]]) # 행렬

cs

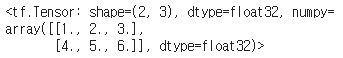
42스칼라 값을 가지는 텐서 생성

1

tf.constant(42) # 스칼라

cs

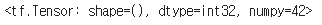
이때, ndarray와 동일하게, tf.Tensor는 크기와 데이터 타입을 가진다. 또한 인덱스 참조 역시 비슷하게 작동한다.

1 2

t.shape t.dtype

cs

가장 중요한 것은 모든 종류의 텐서 연산이 가능하다는 것.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

t + 10   #<tf.Tensor: shape=(2, 3), dtype=float32, numpy= #array([[11., 12., 13.], #       [14., 15., 16.]], dtype=float32)>   tf.square(t)   #<tf.Tensor: shape=(2, 3), dtype=float32, numpy= #array([[ 1.,  4.,  9.], #       [16., 25., 36.]], dtype=float32)>   t @ tf.transpose(t)   #<tf.Tensor: shape=(2, 2), dtype=float32, numpy= #array([[14., 32.], #       [32., 77.]], dtype=float32)

cs

이때, t+10은 tf.add(t,10)을 호출하는 것과 같다. 제곱 연산과, @을 통하여 matmul 행렬곱 가능.

필요한 모든 기본 수학 연산(tf.add(), tf.multiply(), tf.square(), tf.exp(), tf.sqrt() 등)과 넘파이에서 볼 수 있는 대부분의 연산(tf.reshape(), tf.squeeze(), tf.tile())을 제공한다. 그러나 일부 함수들은 넘파이와 이름이 다른 경우가 있다. 이는 넘파이의 함수와 완전히 동일한 작업을 수행하지 않는 경우와 GPU커널이 원소가 추가된 순서를 보장하지 않는 리듀스 알고리즘을 사용하는 경우 때문이 있다.

12.2.2 텐서와 넘파이

텐서는 넘파이와 함께 사용하기 용이하다. 넘파이 배열로 텐서를 만들 수 있고, 그 반대도 가능하다. 또한 넘파이 배열에 텐서플로 연산을 적용할 수 있고, 텐서에 넘파이 연산을 적용할 수 도 있다.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

a = np.array([2., 4., 5.]) tf.constant(a)   # <tf.Tensor: shape=(3,), dtype=float64, numpy=array([2., 4., 5.])>   t.numpy()   #array([[1., 2., 3.], #       [4., 5., 6.]], dtype=float32)   np.array(t)   #array([[1., 2., 3.], #       [4., 5., 6.]], dtype=float32)   tf.square(a)   #<tf.Tensor: shape=(3,), dtype=float64, numpy=array([ 4., 16., 25.])>   np.square(t)   #array([[ 1.,  4.,  9.], #       [16., 25., 36.]], dtype=float32)

cs

12.2.3 타입 변환

타입 변환은 성능을 크게 감소시킬 수 있다. 타입이 자동으로 변환되면 사용자가 눈치재지 못할 수 있어, 이를 방지하기 위하여 텐서플로는 어떤 타입 변환도 자동으로 수행하지 않는다. 호환되지 않는 타입의 텐서로 연산을 실행하면 예외가 발생하는데, 예를 들어 실수 텐서와 정수 텐서를 더할 수 없는 경우나 32비트 실수와 64비트 실수를 더할 수 없는 경우이다.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

try:     tf.constant(2.0) + tf.constant(40) except tf.errors.InvalidArgumentError as ex:     print(ex)   #cannot compute AddV2 as input #1(zero-based) was expected to be a float tensor but is a int32 tensor [Op:AddV2]   try:     tf.constant(2.0) + tf.constant(40., dtype=tf.float64) except tf.errors.InvalidArgumentError as ex:     print(ex)   #cannot compute AddV2 as input #1(zero-based) was expected to be a float tensor but is a double tensor [Op:AddV2]   t2 = tf.constant(40., dtype=tf.float64) tf.constant(2.0) + tf.cast(t2, tf.float32)   #<tf.Tensor: shape=(), dtype=float32, numpy=42.0> Colored by Color Scripter

cs

12.2.4 변수

지금까지 우리가 본 tf.Tensor는 변경이 불가능한 객체이다. 즉, 텐서의 내용을 바꿀 수 없다. 그러나 우리는 역전파로 변경되어야 하는 신경망의 가중치를 계속해서 업데이트 해야 하는데, 이때 필요한 것이 tf.Variable이다.

1 2 3 4 5 6

v = tf.Variable([[1., 2., 3.], [4., 5., 6.]]) v   #<tf.Variable 'Variable:0' shape=(2, 3) dtype=float32, numpy= #array([[1., 2., 3.], #       [4., 5., 6.]], dtype=float32)>

cs

tf.Variable은 tf.Tensor와 비슷하게 동작한다. 동일한 연산을 수행할 수 있으며, 넘파이와도 잘 호환된다. 또한 assign()을 통하여 변수값을 바꿀 수 있다. 원소에 관하여도, 원소의 assign() 메서드나 scatter_update(), scatter_nd_update()를 통하여 개별 원소를 수정할 수도 있다.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

v.assign(2 * v)   #<tf.Variable 'UnreadVariable' shape=(2, 3) dtype=float32, numpy= #array([[ 2.,  4.,  6.], #       [ 8., 10., 12.]], dtype=float32)>   v[0, 1].assign(42)   #<tf.Variable 'UnreadVariable' shape=(2, 3) dtype=float32, numpy= #array([[ 2., 42.,  6.], #       [ 8., 10., 12.]], dtype=float32)>   v[:, 2].assign([0., 1.])   #<tf.Variable 'UnreadVariable' shape=(2, 3) dtype=float32, numpy= #array([[ 2., 42.,  0.], #       [ 8., 10.,  1.]], dtype=float32)>   v.scatter_nd_update(indices=[[0, 0], [1, 2]],                     updates=[100., 200.])   #<tf.Variable 'UnreadVariable' shape=(2, 3) dtype=float32, numpy= #array([[100.,  42.,   0.], #       [  8.,  10., 200.]], dtype=float32)>

cs

12.2.5 다른 데이터 구조

텐서플로는 다음과 같이 몇 가지 다른 데이터 구조도 지원한다.

• 희소 텐서(Sparse tensor, tf.SparseTensor)
  대부분 0으로 채워진 텐서를 효율적으로 나타낸다. tf.sparse패키지를 통해 희소 텐서 연산을 할 수 있다.

• 텐서 배열(Tensor array, tf.TensorArray)
  텐서는 기본적으로 리스트. 고정된 길이를 가지지만 동적으로 바꿀 수 있다. 이때, 리스트에 포함된 모든 텐서는 크기와 데이터 타입이 동일해야 한다.

• 래그드 텐서(Ragged tensor, tf.RaggedTensor)
  래크드 텐서는 리스트의 리스트를 나타낸다. 텐서에 포함된 값은 동일한 데이터 타입을 가져야 하지만 리스트의 길이는 다를 수 있다.

• 문자열 텐서(string tensor)
  tf.string 타입의 텐서. 유니코드가 아닌 바이트 문자열을 사용한다.

• 집합(set)
  집합은 일반적인 텐서로 나타난다. 예를 들면, tf.constant([[1,2],[3,4]])는 두 개의 집합 {1,2}와 {3,4}를 나타낸다. 일반적으로 각 집합은 텐서의 마지막 축에 있는 벡터에 의해 표현된다. tf.sets패키지 사용 가능.

• 큐(queue)
  단계별로 텐서를 저장한다. 텐서플로는 여러 종류의 큐를 제공한다. 이 클래스들은 tf.queue 패키지를 이용하여 사용할 수 있다.

12.3 사용자 정의 모델과 훈련 알고리즘

12.3.1 사용자 정의 손실 함수

여기서는 후버 MSE와 MAE를 절충한 후버 손실을 만들어 사용할 것. 후버 손실은 일정한 범위(델타)를 정해서 그 안에 있으면 오차를 제곱하고, 그 밖에 있으면 오차의 절대값을 구하는 것.

1 2 3 4 5 6

def huber_fn(y_true, y_pred):     error = y_true - y_pred     is_small_error = tf.abs(error) < 1     squared_loss = tf.square(error) / 2     linear_loss  = tf.abs(error) - 0.5     return tf.where(is_small_error, squared_loss, linear_loss)

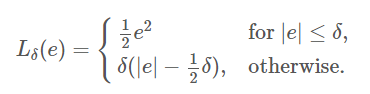
cs

이때, 전체 손실의 평균이 아니라 샘플마다 하나의 손실을 담은 텐서를 반환하는 것이 좋다. 이렇게 해야 필요할 때 케라스가 클래스 가중치나 샘플 가중치를 적용할 수 있다. 이제 이렇게 만들어진 Loss function을 이용하여 모델 훈련한다.

1 2 3 4

model.compile(loss=huber_fn, optimizer="nadam", metrics=["mae"])   model.fit(X_train_scaled, y_train, epochs=2,           validation_data=(X_valid_scaled, y_valid))

cs

12.3.2 사용자 정의 요소를 가진 모델을 저장하고 로드하기

케라스가 함수 이름을 저장하므로, 사용자 정의 손실 함수를 사용하는 모델은 아무 이상 없이 저장되는데, 모델을 로드할 때는 함수 이름과 실제 함수를 매핑한 딕셔너리를 전달해야 한다. 좀 더 일반적으로 사용자 정의 객체를 포함한 모델을 로드할 때는 그 이름과 객체를 매핑해야 한다.

1 2

model = keras.models.load_model("my_model_with_a_custom_loss.h5",                                 custom_objects={"huber_fn": huber_fn})

cs

앞서 구현한 함수는 -1과 1 사이의 오차는 작은 것으로 간주하는데, 이때 다른 기준이 필요하다면 어떻게 해야 할까. 이는 매개변수를 받을 수 있는 함수를 만드는 것으로 해결할 수 있다.

1 2 3 4 5 6 7 8

def create_huber(threshold=1.0):     def huber_fn(y_true, y_pred):         error = y_true - y_pred         is_small_error = tf.abs(error) < threshold         squared_loss = tf.square(error) / 2         linear_loss  = threshold * tf.abs(error) - threshold**2 / 2         return tf.where(is_small_error, squared_loss, linear_loss)     return huber_fn Colored by Color Scripter

cs

이 모델을 저장할 때, threshold값은 저장되지 않으므로, 모델을 로드할 때 threshold값을 지정해주어야 한다.

1 2

model = keras.models.load_model("my_model_with_a_custom_loss_threshold_2.h5",                                 custom_objects={"huber_fn": create_huber(2.0)})

cs

이러한 문제는 결론적으로 keras.losses.Loss 클래스를 상속하고 get_config()메서드를 구현하여 해결할 수 있다.

1 2 3 4 5 6 7 8 9 10 11 12 13

class HuberLoss(keras.losses.Loss):     def __init__(self, threshold=1.0, **kwargs):         self.threshold = threshold         super().__init__(**kwargs)     def call(self, y_true, y_pred):         error = y_true - y_pred         is_small_error = tf.abs(error) < self.threshold         squared_loss = tf.square(error) / 2         linear_loss  = self.threshold * tf.abs(error) - self.threshold**2 / 2         return tf.where(is_small_error, squared_loss, linear_loss)     def get_config(self):         base_config = super().get_config()         return {**base_config, "threshold": self.threshold}

cs

이렇게 한다면, 모델을 저장할 때 임계값도 함께 저장된다. 이에 모델을 로드할 때 클래스 이름과 클래스 자체를 매핑해주어야 한다.

12.3.3 활성화 함수, 초기화, 규제, 제한을 커스터마이징 하기

다음은 사용자 정의 활성화 함수, 사용자 정의 글로럿 초기화, 사용자 정의 l1-규제, 양수인 가중치만 남기는 사용자 정의 제한이나 tf.nn.relu()에 대한 예시이다.

이렇게 만들어진 사용자 정의 함수는 보통의 함수와 동일하게 아래처럼 사용할 수 있다.

1 2 3 4

layer = keras.layers.Dense(1, activation=my_softplus,                            kernel_initializer=my_glorot_initializer,                            kernel_regularizer=my_l1_regularizer,                            kernel_constraint=my_positive_weights)

cs

이 활성화 함수는 Dense 층의 출력에 적용되고 다음 층에 그 결과가 전달되고, 그 다음 층에 그 결과가 전달된다. 층의 가중치는 초기화 함수에서 반환된 값으로 초기화되고 훈련 스텝마다 가중치가 규제 함수에 전달되어 규제 손실을 계산하고 전체 손실에 추가되어 훈련을 위한 최종 손실을 만든다. 마지막으로 제한 함수가 훈련 스텝마다 호출되어 층의 가중치를 제한한 가중치 값으로 바뀐다.

만약, 함수가 모델과 함께 저장해야 할 하이퍼 파라미터를 가진다면 적절한 클래스를 상속하게 한다. 다음은 factor 하이퍼 파라미터를 저장하는 l1 규제를 위한 간단한 클래스의 예이다.

1 2 3 4 5 6 7

class MyL1Regularizer(keras.regularizers.Regularizer):     def __init__(self, factor):         self.factor = factor     def __call__(self, weights):         return tf.reduce_sum(tf.abs(self.factor * weights))     def get_config(self):         return {"factor": self.factor}

cs

12.3.4 사용자 정의 지표

손실과 지표는 개념적으로 다른 것은 아니다. 손실은 모델을 훈련하기 위해 경사 하강법에서 사용하므로 미분이 가능해야 하고 Gradient가 모든 곳에서 0이 아니어야 하며 사람이 쉽게 이해할 수 없어도 괜찮다. 반대로 지표는 모델을 평가할 때 사용한다. 이에 미분이 가능하지 않거나, 모든 곳에서 Gradient가 0이어도 괜찮으며 또한 사람이 쉽게 이해할 수 있어야 한다.

그러나, 사용자 지표 함수를 만드는 것은 사용자 손실 함수를 만드는 것과 동일하다.

지표함수를 만들 때에는 정밀도를 계산할 수 있는 객체가 필요하다. 이는 keras.metrics.Precision을 이용하여 가능. 이는 배치마다 점진적으로 업데이트 되기 때문에, 이를 스트리밍 지표라고 한다.

1 2 3 4 5 6

model.compile(loss="mse", optimizer="nadam", metrics=[create_huber(2.0)])   precision = keras.metrics.Precision() precision([0, 1, 1, 1, 0, 1, 0, 1], [1, 1, 0, 1, 0, 1, 0, 1])   #<tf.Tensor: shape=(), dtype=float32, numpy=0.8>

cs

이 지점에서 result()메서드를 호출하여 현재 지표값을 얻을 수 있고, variables 속성을 사용하여 변수를 확인할 수도 있다. 또한 reset_states() 메서드를 사용해 초기화도 가능.