DFS

깊이 우선 탐색(DFS, Depth-First Search)이란?

그래프 탐색 알고리즘 중 하나로 한 방향으로 갈 수 있을 때까지 최대한 깊게 탐색한 후 더 이상 갈 수 없게 되면, 다시 돌아와 다음 경로를 탐색하는 방식을 의미

• 기본적인 수행과정은 한 노드에서 시작하여 가능한 한 깊숙이 탐색한 후, 다음 분기로 넘어간다
  그리고 더 이상 탐색할 수 없는 상태에 도달하면, 이전으로 돌아가서 다른 가능한 분기를 탐색한다
• ‘모든 정점을 방문’하고 연결된 모든 간선을 검사하기 때문에 그래프의 모든 구성 요소를 탐색(완전 탐색)하거나 특정 조건을 만족하는 경로를 찾을 때 유용하다

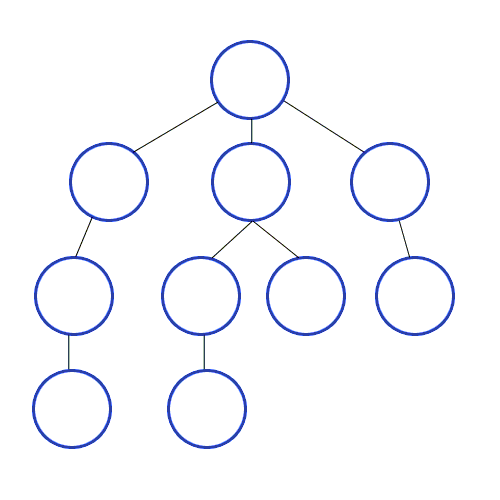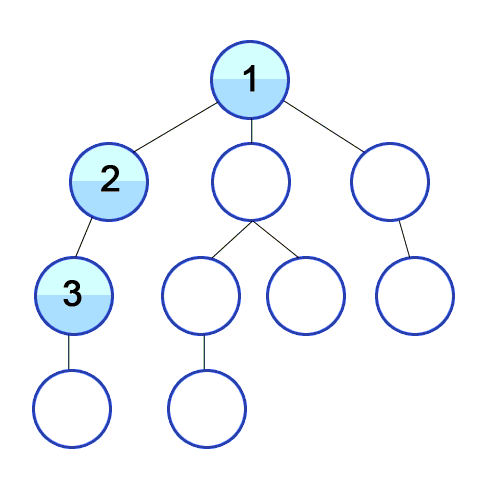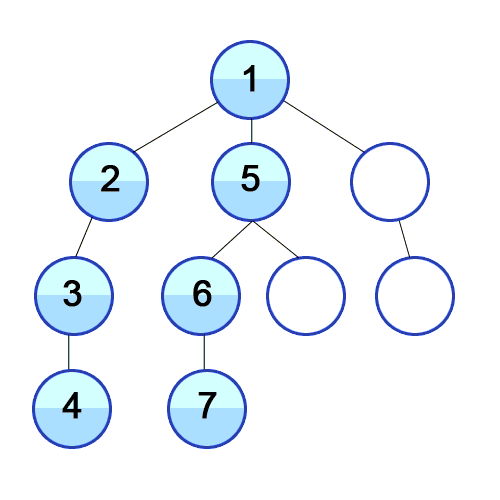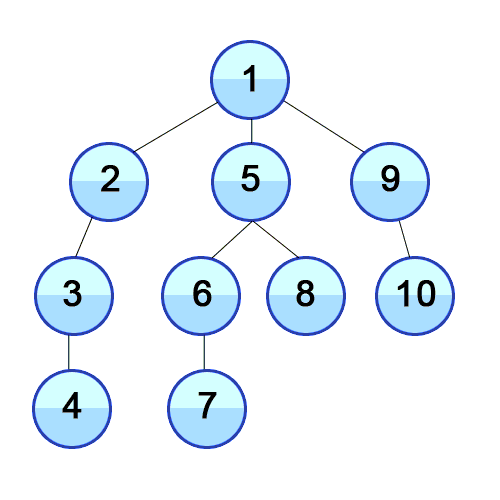
깊이 우선 탐색에 사용되는 주요 용어

• 그래프(Graph)

  정점과 간선의 집합으로 구성되어 있으며 정점은 서로 다른 정점과 연결된 구조를 가지는 형태

• 정점 (Vertices)

  그래프에서 ‘데이터’를 나타내는 개별 요소, 노드(Node)라고도 불린다

• 간선(Edge)

  그래프에서 ‘정점간의 관계’를 나타내는 선, 연결선이라고도 불린다

• 분기(Branching)

  특정 노드에서 후퇴하기 전에 가능한 모든 경로를 탐색하는 과정

• 방문한 노드(Visited Node)

  이미 탐색되어 처리된 정점

• 미 방문 노드(Unvisited Node)

  아직 탐색되지 않은 정점

• 인접한 노드(Adjacent Node)

  그래프에서 특정한 노드와 연결된 노드 즉, 어떤 노드와 간선(edge)으로 직접 연결되어 있는 다른 노드

DFS의 특징

1. 깊이 우선 탐색 방법

• 스택(Stack) 또는 재귀(Recursion)를 사용하여 구현할 수 있다
• 탐색을 시작한 정점을 스택에 push하고, 해당 정점과 연결된 정점들을 차례로 방문
• 그래프의 구조를 재귀적으로 탐색하므로, 재귀 호출을 사용하는 경우 스택 오버플로우에 유의해야 한다

2. 탐색 과정

깊이우선 탐색은 한 정점에서 시작하여 최대한 깊게 탐색한 후, 더 이상 방문할 수 있는 정점이 없을 경우 이전 정점으로 돌아와 다른 경로로 탐색, 이 과정을 반복하여 그래프의 모든 정점을 탐색

3. 경로의 길이를 고려하지 않는다

   • 최단 경로를 찾는 문제와는 다르게, 경로의 길이를 고려하지 않는다

• 탐색을 시작한 정점에서부터 가능한 한 깊이까지 탐색하기 때문에, 최단 경로를 찾는 문제에는 다른 알고리즘을 사용해야 한다

4. 구현이 간단

   • 깊이우선 탐색은 재귀적인 특성을 가지고 있어 구현이 간단

• 하지만 그래프의 깊은 부분을 탐색할 경우에는 스택 오버플로우(Stack Overflow)가 발생할 수 있으므로, 반복적인 구현이 필요할 수도 있다 -> 백트래킹과 함께 써서 해소 가능

그래프와 DFS

• 입력으로 아래와 같이 주어질 때
  

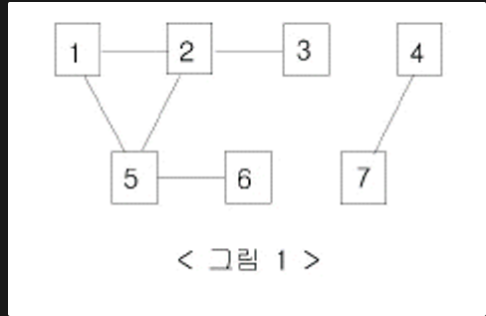
7
6
1 2
2 3
1 5
5 2
5 6
4 7

• 아래와 같이 구현 할 수 있다

  public static void dfs(
      int[][] graph,
      boolean[] visited,
      int start
  ) {
    Stack<Integer> stack = new Stack<>();
    stack.push(start);
    visited[start] = true;
    System.out.println(start);

    while (!stack.isEmpty()) {
      int vertex = stack.pop();

      for (int i = 1; i < graph.length; i++) {
        if (graph[vertex][i] == 1 && !visited[i]) {
          stack.push(i);
          visited[i] = true;
          System.out.println(i);
        }
      }
    }
  }