이진 탐색

이진 탐색(Binary Search)이란?

• 정렬된 배열에서 특정 값을 찾는 알고리즘
• 이진탐색은 탐색 범위를 절반씩 줄여나가기 때문에 선형탐색에 비해 빠른 속도를 보장하지만
  배열이 정렬되어 있어야 한다는 조건이 필요하다

선형탐색(Linear Search)이란?

• 배열이나 리스트와 같은 데이터 구조에서 특정한 값을 찾는 알고리즘 중 하나

---

이진 탐색 이해하기

이진 탐색 과정

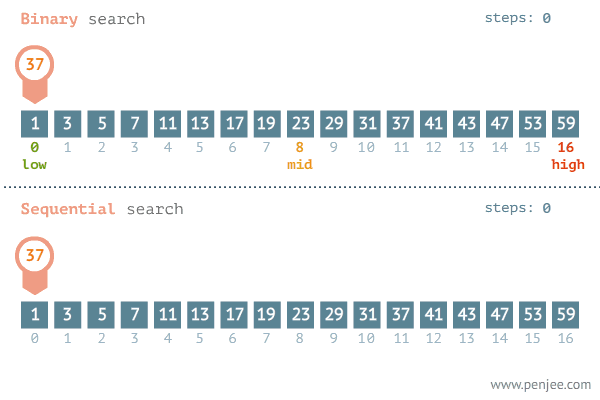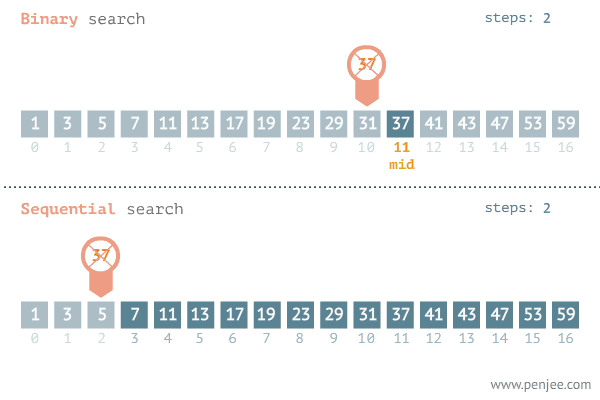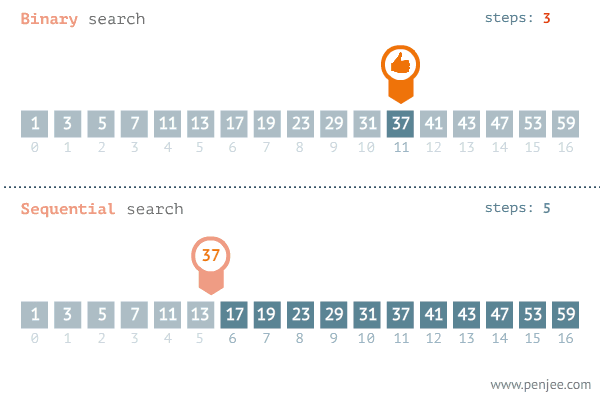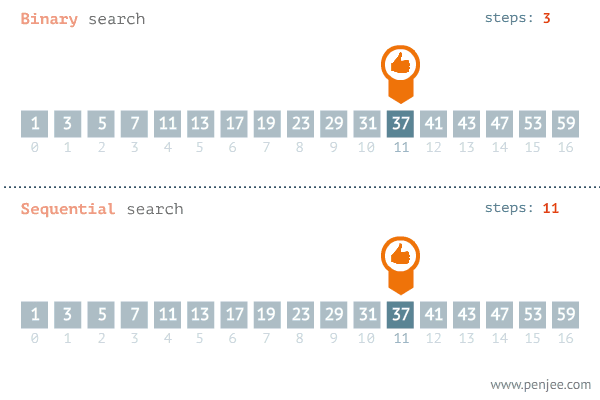
1. 배열의 '중간 값'을 선택하여 찾고자 하는 값과 비교

2. 만약 중간 값이 찾고자 하는 값보다 크면 '배열 왼쪽 부분'에서 탐색을 진행,
   값보다 작으면 '배열 오른쪽 부분'에서 탐색을 진행

3. 이 과정에서 찾고자 하는 값이 나올 때까지 반복

이진 탐색과 for문(선형 탐색)의 차이점

• 일반적으로 이진 탐색을 이용하여 값을 찾는 방법이 for문을 이용하는 것보다 빠르다

• 이진 탐색은 중간값을 찾아 탐색 범위를 반으로 줄이면서 값을 찾아간다

• for문은 전체를 순회하면서 값을 찾기 때문에, 배열의 크기와 상관없이 속도가 일정하게 증가한다

이진탐색을 언제 사용해야 하는가?

• 데이터가 오름차순으로 정렬되어 있을 때 특정한 값을 찾아야 한다면 사용하는게 좋다
• 데이터의 양이 많을 경우에도 빠른 시간 내에 값을 찾을 수 있다

이진탐색의 성능

O(logn)

• 다른 정렬에 비해 상대적으로 매우 빠르다

예시

int[] arr = {1, 3, 5, 8, 11, 15, 30, 32, 45}이고 key 값이 8인 경우 찾기

• while문 이용

 	int answer = 0;
    // [STEP1] 시작 인덱스와 마지막 인덱스 값을 지정
    int start = 0;
    int end = arr.length - 1;

    // [STEP2] 마지막 인덱스를 보다 첫번째 인덱스가 같아지거나 작을 경우까지 순회
    while (start <= end) {

        // [STEP3] 중간 값을 구합니다.
        int mid = (start + end) / 2;

        // [CASE4-1] 중간 값보다 찾으려는 값(key)가 큰 경우 : 중간 값에 1을 더하여 오른쪽 절반을 탐색
        if (arr[mid] < key) {
            start = mid + 1;
        }
        // [CASE4-2] 중간 값보다 찾으려는 값(key)가 작은 경우 : 중간값에 1을 빼서 왼쪽 절반을 탐색
        else if (arr[mid] > key) {
            end = mid - 1;
        }
        // [CASE4-3] 해당 경우가 아니면 중간값을 최종 값으로 반환
        else {
            answer = mid;
        }
    }
    // [STEP5] 최종 탐색을 하지 못할 경우 -1을 반환
    if (answer == 0) answer = -1;

• 재귀함수 이용

public static int binarySearch(int[] arr, int start, int end, int key) {
    // 1. 높은 인덱스가 낮은 인덱스보다 크거나 같은지 확인
    if (end >= start) {

        // 2. 중간 값을 구하기
        int mid = low + (end - start) / 2;

        // 3. 배열의 요소 값이 찾는 값과 동일하면 중간 값을 반환
        if (arr[mid] == key) {
            return mid;
        }
        // 4. 중간 값이 키보다 큰 경우 : 낮은 인덱스와 중간 인덱스에서 1을 뺀 값을 가지고 함수를 재귀적으로 호출
        else if (arr[mid] > key) {
            return binarySearch(arr, start, mid - 1, key);
        }
        // 5. 중간 값이 키보다 작은 경우 : 중간 인덱스에 1을 더하고 높은 인덱스와 함께 함수를 재귀적으로 호출
        else {
            return binarySearch(arr, mid + 1, end, key);
        }
    }

    // 6. 높은 인덱스가 낮은 인덱스보다 작으면 배열에서 키를 찾지 못했음을 나타내기 위해 -1을 반환
    return -1;
}

Arrays.binarySearch()

매개변수로 주어진 배열에서 원하는 값을 이진 탐색하여 인덱스를 반환,
만약 해당 원소가 배열에 없다면 음수를 반환,
이진 탐색을 하기 전에 반드시 배열을 정렬해야 한다

int binarySearch(Object[] a, Object key)

멘토님께 받은 정형화된 풀이