PyTorch 소프트맥스 회귀

• 자료출처 : PyTorch로 시작하는 딥 러닝 입문

소프트맥스 회귀

• 소프트 맥스 회귀는 다중 클래스 분류(3개 이상의 선택지로부터 1개를 선택)를 풀기위한 알고리즘

1. 원-핫 인코딩(One-hot encoding)

• 선택지의 갯수만큼 차원을 가지면서, 각 선택지를 0 과 1로 표현
• 원-핫 인코딩이 된 벡터의 예시
  • 강아지 = [1, 0, 0]
  • 고양이 = [0, 1, 0]
  • 냉장고 = [0, 0, 1]
• 대부분의 다중 클래스 분류 문제가 각 클래스 간의 관계가 균등하다는 점에서 원-핫 벡터는 이러한 점을 표현할 수 있는 적절한 표현방법

1. 소프트맥스 함수

• 소프트맥스 함수는 분류해야하는 정답지(클래스)의 총 개수를 k라고 할 때,
• k차원의 벡터를 입력받아 각 클래스에 대한 확률을 추정
• 3개의 차원을 가진 소프트맥스 함수는 아래와 같다

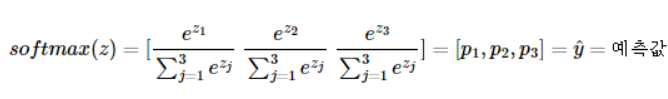
클래스가 k(위 식에선 3개)개 일때, k차원의 벡터를 입력받아 모든 벡터 원소의 값을 0과 1사이의 값으로 변경하여 다시 k차원의 벡터를 리턴

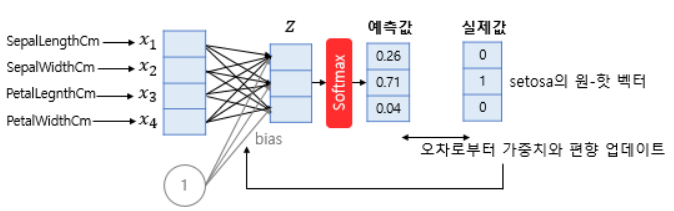
• 위 그림은 아이리스 꽃의 4개의 특성을 통해 3개의 품종 중 무엇일지 예측하는 모델이다.
• 4개의 독립변수를 모델이 4차원 벡터로 입력받아 소프트맥스 함수를 통해 3차원 벡터로 표현함

2. 비용함수

• 소프트맥스 회귀에서는 비용 함수로 크로스 엔트로피 함수를 사용

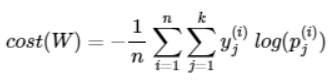
• n은 전체 데이터의 갯수, y는 실제값, k는 클래스 개수, j는 클래스의 인덱스, p는 확률을 의미
• 만약 j의 실제값이 원-핫 벡터에서 1을 가진 인덱스라면, Pj = 1이 될 것이고 log(1) = 0 이 된다.
• 결과적으로 정확하게 예측한 경우 크로스 엔트로피 함수의 값은 0이 되므로, 크로스 엔트로피 함수를 최소화하는 방향으로 학습해야 한다.

파이토치로 소프트맥스 비용함수 구현

import torch
import torch.nn.functional as F

torch.manual_seed(1)

<torch._C.Generator at 0x278878b55f0>

# 임의의 3x5 크기의 텐서 생성
z = torch.rand(3, 5, requires_grad=True)

# 각 샘플에 임의의 레이블 생성
y = torch.randint(5, (3,)).long()
print(y)

tensor([3, 1, 2])

F.cross_entropy(z, y)

tensor(1.4992, grad_fn=<NllLossBackward0>)

• nll은 Nagative Log Likelihood의 약자로 F.log_softmax() 수행 후 남은 수식들을 수행
• F.cross_entropy()는 F.log_softmax()와 F.nll_loss()를 포함하고 있음

3. 소프트맥스 회귀 구현

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

torch.manual_seed(1)

<torch._C.Generator at 0x278878b55f0>

# 훈련 데이터와 레이블 텐서로 선언
x_train = [[1, 2, 1, 1],
           [2, 1, 3, 2],
           [3, 1, 3, 4],
           [4, 1, 5, 5],
           [1, 7, 5, 5],
           [1, 2, 5, 6],
           [1, 6, 6, 6],
           [1, 7, 7, 7]]
y_train = [2, 2, 2, 1, 1, 1, 0, 0]
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)

• x_train의 샘플은 4개의 특성을 가지고 있으며, 총 8개의 샘플이 존재 (8 x 4)
• y_train은 각 샘플에 대한 레이블(8 x 1)인데, 여기서는 0,1,2의 3개의 클래스 존재
• 클래스가 3개 이므로 원-핫 인코딩의 결과는 8 x 3의 갯수를 가져야 함

y_one_hot = torch.zeros(8, 3)
y_one_hot.scatter_(1, y_train.unsqueeze(1), 1)
print(y_one_hot.shape)

torch.Size([8, 3])

# 모델 초기화
W = torch.zeros((4, 3), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer는 경사하강법
optimizer = optim.SGD([W, b], lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

    # Cost 계산
    z = x_train.matmul(W) + b
    cost = F.cross_entropy(z, y_train)

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    # 100번마다 로그 출력
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))

Epoch    0/1000 Cost: 1.098612
Epoch  100/1000 Cost: 0.761050
Epoch  200/1000 Cost: 0.689991
Epoch  300/1000 Cost: 0.643229
Epoch  400/1000 Cost: 0.604117
Epoch  500/1000 Cost: 0.568255
Epoch  600/1000 Cost: 0.533922
Epoch  700/1000 Cost: 0.500291
Epoch  800/1000 Cost: 0.466908
Epoch  900/1000 Cost: 0.433507
Epoch 1000/1000 Cost: 0.399962